Using Planck's fromula, derive the approximate expressions for the space spectral density uω of radiation
(a) in the range where hω<<kT (Rayleigh-Jeans fromula),
(b) in the range where hω>>kT (Wien's formula).
From Planek's formula
u_(omega) = (cancelh omega^(2))/(pi^(2)c^(3))(1)/(c^(homega//k)-1)
(a) In a range hω<<kT (long wavelength or high temperature).
u_(omega) rarr (cancel homega^(3))/(pi^(2)c^(3))(1)/((cancelh omega)/(kT))
=ω2π2c3kT, using ex=1+x for small x.
(b) In the range cancelh omega gt gtT (high frequency ot low temperature):
(cancelh omega)/(kT)gt gt 1 so e^((cancelh omega)/(kT)) gt gt 1
and u_(omega) = (cancelhomega^(3))/(pi^(2)c^(3))e^(-cancelh omega//kT)
Topper's Solved these Questions
- OPTICSBook:IE IRODOV, LA SENA & SS KROTOVChapter:OPTICSExercise:Exercise
Explore 2 Videos
- OPTICSBook:IE IRODOV, LA SENA & SS KROTOVChapter:OPTICSExercise:Optics Of Moving Sources
Explore 22 Videos
- MECHANICSBook:IE IRODOV, LA SENA & SS KROTOVChapter:MECHANICSExercise:Mechanics Problems
Explore 92 Videos
- OSCILLATIONS AND WAVESBook:IE IRODOV, LA SENA & SS KROTOVChapter:OSCILLATIONS AND WAVESExercise:Electromagnetic Waves, Radiation
Explore 36 Videos
Similar Questions
Using Wien's formula, demonstrate that
(a) the most probable radiation frequency ωpr∝t,
(b) the maximum spectral density of thermal radiation (uω)max∝T3,
(c ) the radiosity Me∝T4.
View SolutionFind the dimensional formulae of the following quantities:
(a) the resistance R
(b) the inductance L
© the magnetic field B
(d) the permeability of free space μ0
(e) the magnetic dipole moment M
(f) Planck' s constant h
some formulae containing these qunatities are
V=iR,U=12Li2,F=Bil,B=μi02r,M=iA,E=hv
where V:electric potential, i: electric current, F: force, l:length r: radius, A area, E: energy, v: frequency and U: energy.
View Solution
Knowledge Check
Formula A: BMI=wh2
Formula B: BMI=4w−1005
The formulas above are used in nutrition to estimate the body mass index BMI, in kilograms per square meter, of adults whose weight w ranges between 50 and 100 kilograms and whose height h is measured in meters.
Based on formula B, what is w in terms of BMI?
IF both formulas A and B give the same estimate for BMI, which of the following expressions is equivalent to 4w-100?Awh2B5wh2C5w4h2D5w+1004h2When a liquid is completely miscible with another liquid, a homogeneous solution consisting of a single phase is formed. If such a solution is placed in a closed evacuated vessel, the total pressure exerted by the vapour, after the system attained equilibrium will be equal to the sum of partial pressures of the constituents. A solution is said to be ideal if its constituents follow Raoult's law under all conditions of concentrations, i.e., where pi is the partial pressures of the constituent i, whose mole fraction in the solution is xi and p∘i is the corresponding vapour pressure of the pure constituent. The change in the thermodynamic functions when an ideal solution is formed by mixing pure components is given by the following expression.
Δmix=G=ntotalRT∑ixiInxi ...(i)
where, ntotal is the total amount of all the constituents present in the solution.
ΔmixF=−ntotalR∑ixiInxi ......(ii)
ΔmixH=−ntotalRT∑ixiInxi−ntotalR∑ixiInxi=0 ........(iii)
ΔmixU=0 .........(iv)
Since botli the components of an ideal binary system follow Raoult's law of the entire range of the compositions, the partial pressure exerted by the vapours of these constituents over the solution will be given by
pA=xAp∘A ..........(v)
pB=xBp∘B .........(vi)
where, xA and xB are the mole fractions of the two constituents in the liquid phase and p∘A and p∘B are the respective vapour pressure of the pure constituents. The total pressure (p) over the solution will be the sum of the partial pressure. The composition of the vapour phase (yA) can be determined with the help of Dalton's law of partial pressures.
For an ideal solution in which p∘A>p∘B, the plot of total pressure (p) us the mole fraction of A at constant temperature in the vapour phase is:A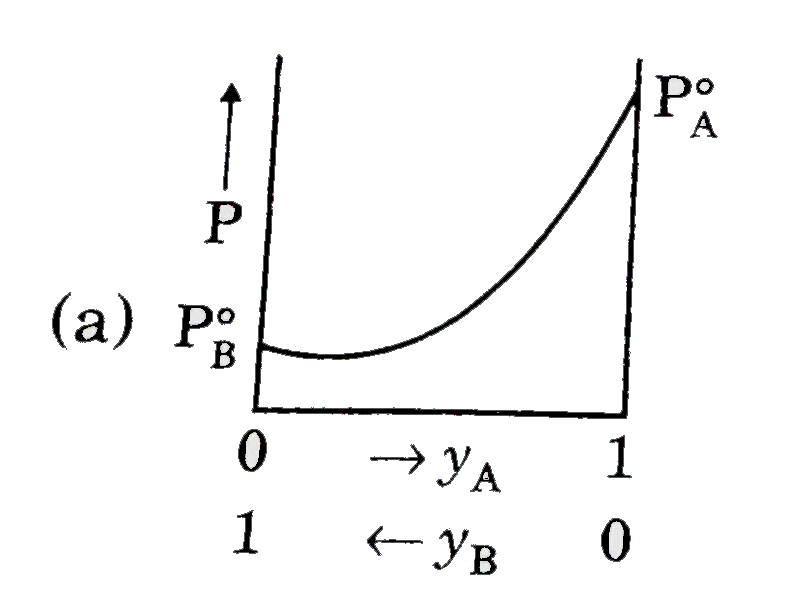 B
B C
C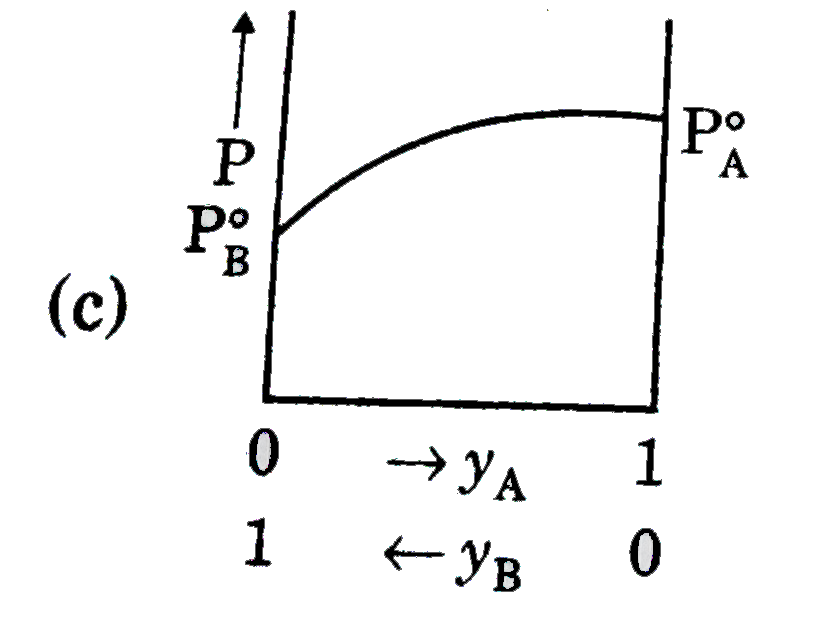 D
D
When a liquid is completely miscible with another liquid, a homogeneous solution consisting of a single phase is formed. If such a solution is placed in a closed evacuated vessel, the total pressure exerted by the vapour, after the system attained equilibrium will be equal to the sum of partial pressures of the constituents. A solution is said to be ideal if its constituents follow Raoult's law under all conditions of concentrations, i.e., where pi is the partial pressures of the constituent i, whose mole fraction in the solution is xi and p∘i is the corresponding vapour pressure of the pure constituent. The change in the thermodynamic functions when an ideal solution is formed by mixing pure components is given by the following expression.
Δmix=G=ntotalRT∑ixiInxi ...(i)
where, ntotal is the total amount of all the constituents present in the solution.
ΔmixF=−ntotalR∑ixiInxi ......(ii)
ΔmixH=−ntotalRT∑ixiInxi−ntotalR∑ixiInxi=0 ........(iii)
ΔmixU=0 .........(iv)
Since botli the components of an ideal binary system follow Raoult's law of the entire range of the compositions, the partial pressure exerted by the vapours of these constituents over the solution will be given by
pA=xAp∘A ..........(v)
pB=xBp∘B .........(vi)
where, xA and xB are the mole fractions of the two constituents in the liquid phase and p∘A and p∘B are the respective vapour pressure of the pure constituents. The total pressure (p) over the solution will be the sum of the partial pressure. The composition of the vapour phase (yA) can be determined with the help of Dalton's law of partial pressures.
A plot of reciprocal of total pressure (1p) (y-axis) us yA (x-axis) gives :Aa linear plot with slope =(1p∘B−1p∘A)Ba linear plot with slop =(1p∘A−1p∘B)Ca linear plot with slope =1p∘BDa linear plot with slope =p∘Ap∘B
At a temperature of 0K, the total energy of a gaseous diatomic molecule AB is approximately given by:
E=Eo+Evib
where Eo is the electronic energy of the ground state, and Evib is the vibrational energy.
Allowed values of the vibrational energies are given by the expression:
Evid=(v−12)ε v=0,1,2,....... ε=h2π√kμ μ(AB)=mAmBmA+mB
where h is the planck's constant, is the vibration quantum number, k is the force constant, and is the reduced mass of the molecule. At 0K, it may be safely assumed that is zero, and Eo and k are independent of isotopic substitution in the molecule.
Deuterium, D, is an isotope of hydrogen atom with mass number 2. For the H2 molecule, k is 575.11Nm−1, and the isotopic molar masses of H and D are 1.0078 and 2.0141gmol−1, respectively.
At a temperature of 0K:εH2=1.1546εHD and εD2=0.8167εHD
Calculate––––––––––– the electron affinity, EA, of H+2 ion in eV if its dissociation energy is 2.650eV. If you have been unable to calculate the value for the dissociation energy of H2 then use 4.500eV for the calculate.
View SolutionAt a temperature of 0K, the total energy of a gaseous diatomic molecule AB is approximately given by:
E=Eo+Evib
where Eo is the electronic energy of the ground state, and Evib is the vibrational energy.
Allowed values of the vibrational energies are given by the expression:
Evid=(v−12)ε v=0,1,2,....... ε=h2π√kμ μ(AB)=mAmBmA+mB
where h is the planck's constant, is the vibration quantum number, k is the force constant, and is the reduced mass of the molecule. At 0K, it may be safely assumed that is zero, and Eo and k are independent of isotopic substitution in the molecule.
Deuterium, D, is an isotope of hydrogen atom with mass number 2. For the H2 molecule, k is 575.11Nm−1, and the isotopic molar masses of H and D are 1.0078 and 2.0141gmol−1, respectively.
At a temperature of 0K:εH2=1.1546εHD and εD2=0.8167εHD
Calculate––––––––––– the electron affinity, EA, of H+2 ion in eV if its dissociation energy is 2.650eV. If you have been unable to calculate the value for the dissociation energy of H2 then use 4.500eV for the calculate.
View SolutionAssuming the spectral distribution of thermal radiation energy of obey wien's formula u(ω,T)=Aω3exp(−1ω/T), where a=7.64ps.K, find for a temperature T=2000K the most probable
(a) radiation frequency, (b) radiation wavelength.
View SolutionWhen a liquid is completely miscible with another liquid, a homogeneous solution consisting of a single phase is formed. If such a solution is placed in a closed evacuated vessel, the total pressure exerted by the vapour, after the system attained equilibrium will be equal to the sum of partial pressures of the constituents. A solution is said to be ideal if its constituents follow Raoult's law under all conditions of concentrations, i.e., where pi is the partial pressures of the constituent i, whose mole fraction in the solution is xi and p∘i is the corresponding vapour pressure of the pure constituent. The change in the thermodynamic functions when an ideal solution is formed by mixing pure components is given by the following expression.
Δmix=G=ntotalRT∑ixiInxi ...(i)
where, ntotal is the total amount of all the constituents present in the solution.
ΔmixF=−ntotalR∑ixiInxi ......(ii)
ΔmixH=−ntotalRT∑ixiInxi−ntotalR∑ixiInxi=0 ........(iii)
ΔmixU=0 .........(iv)
Since botli the components of an ideal binary system follow Raoult's law of the entire range of the compositions, the partial pressure exerted by the vapours of these constituents over the solution will be given by
pA=xAp∘A ..........(v)
pB=xBp∘B .........(vi)
where, xA and xB are the mole fractions of the two constituents in the liquid phase and p∘A and p∘B are the respective vapour pressure of the pure constituents. The total pressure (p) over the solution will be the sum of the partial pressure. The composition of the vapour phase (yA) can be determined with the help of Dalton's law of partial pressures.
Two liquids A and B form an ideal solution at temperature T. when the total vapour pressure above the solution is 600 torr, the mole fraction of A in the vapour phase is 0.35 and in the liquid phase 0.70. The vapour pressure of pure B and A are:
View Solutionthe only electron in the hydrogen atom resides under ordinary conditions in the first orbit. When energy is supplied the electron moves to higher energy orbit depending on the amount of energy absorbed. It emits energy. Lyman series is formed when the electron returns to the lowest orbit while Balmer series is formed when the electron returns to second. Similarly, Paschen, Breakett and Pfund series are formed when electron returns to the third, fourth and fifth orbits from higher energy orbits respectively (as shown in figure).
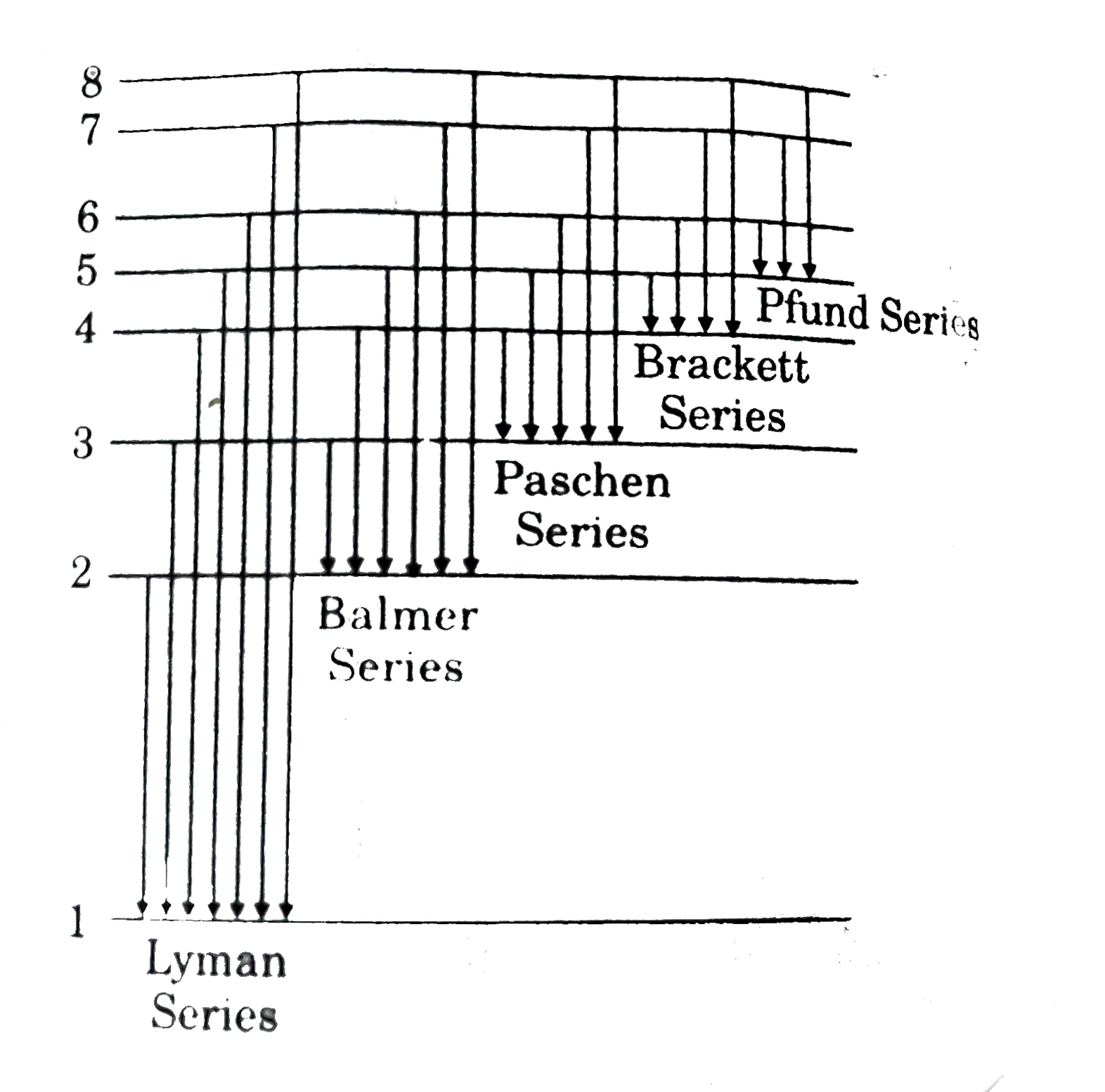
Maximum number of different lines produced when electron jump from nth level to ground level is equal to
n(n−1)2.
For example in the case of n=4, number of lines produced is 6.(4→3,4→2,4→1,3→2,3→1,2→1).When an electron returns from n2ton1 state, the number of different
lines in the spectrum will be equal to (n2−n1)(n2−n1+1)2
If the electron comes back from energy level having energy E2 to energy level having energy E1, then the difference may be expressed in terms of energy of photon as:
E2−E1=ΔE,λ=hcΔE,ΔE=hv(v−frequency)
Since h and c are constants ΔE corresponds to definite energy: thus each transition from one energy level to another will produce a light of definite wavelength. This is actually observed as a line in the spectrum of hydrogen atom.
Wave number of line is given by the formula:
¯v=RZ2(1n21−1n22)
where R is a Rydberg constant (R=1.1×107m−1).
(i) First line of a series : It is called line of longest wavelength of line of smallest energy'.
(ii) Series limit or last line of a series : It is the line of shortest wavelength or line of highest energy.
Consider the following statements
(i) Spectral lines of He+ion belonging to Balmer series are not in visible range.
(ii) In the Balmer series of H-atom maximum lines are in ultraviolet ragion.
(iii) 2nd line of Lyman series of He+ ion has energy 48.35eV
The above statement (i), (ii), (iii) respectively are(T=True,F=False):
View Solution
