A cavity of volume V=1.01 is filled with thernal radiation at a temperature T=1000K. Find:
(a) the heat capacity Cv, (b) the entropy S of that radiation.
(a) The total internal energy of the cavity is
U=4σcT4V
Hence Cv=(∂U∂T)v=16σCT3V
=16×5.67×1083×108×109×10−3Joule/∘K
=1.6×5.673nJ/K=3.024nJ/K
(b) From first law
TdS=dU+pdV
=VdU+UdV+u3dV(p=U3)
=VdU+4U3dV
=16σCVT3dT+16σ3CT4dV
or dS=16σCVT2dT+16σ3CT3dV
=(16σ3CVT3)
Hence S=16σ3CVT3=13Cv=1.008nJ/K.
Topper's Solved these Questions
- OPTICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - OPTICSEXERCISE - Exercise
2 Videos
- OPTICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - OPTICSEXERCISE - Optics Of Moving Sources
22 Videos
- MECHANICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - MECHANICSEXERCISE - Mechanics Problems
92 Videos
- OSCILLATIONS AND WAVESBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - OSCILLATIONS AND WAVESEXERCISE - Electromagnetic Waves, Radiation
36 Videos
Similar Questions
One mole of an ideal gas with heat capacity CV goes through a process in which its entropy S depends on T as S=α/T, where α is a constant. The gas temperature varies from T1 to T2 Find :
(a) the molar heat capacity of the gas as function of its temperature ,
(b) the amount of heat transferred to the gas ,
( c) the work performed by the gas.
View SolutionA chunk of ice of mass m1=100g at a temperature t1=100g was at a temperature t2. Assuming the heat capacity of the calorimeter to be negligible, find the entropy increment of the system by the moment the thermal equilibrium is reached. Consider two cases :
(a) t2=60∘C ,
(b) t2=94∘C.
View Solution
Knowledge Check
A heated body maitained at T K emits thermal radiation of total energy E with a maximum intensity at frequency v. The emissivity of the material is 0.5. If the temperature of the body be increased and maintained at temperature 3T K, then :-
(i) The maximum intensity of the emitted radiation will occur at frequency v/3
(ii) The maximum intensity of the emitted radiation will occur at frequency 3v.
(iii) The total energy of emitted radiation will become 81 E
(iv) The total energy of emitted radiation will become 27 EAi & iiBii & iiiCi & ivDi, ii & ivA body at higher temperature T K radiates heat at a rate which is proportional to
ATBT2CT−4DT4Among the quantities, density (p), temperature (T), heat capacity (Cp), volume (V) and pressure (P), a set of intensive variables are-
A(p, T, H)B(H, T, V)C(V,T,Cp)D(p, T, P)
A heated body maitained at T K emits thermal radiation of total energy E with a maximum intensity at frequency v. The emissivity of the material is 0.5. If the temperature of the body be increased and maintained at temperature 3T K, then :-
(i) The maximum intensity of the emitted radiation will occur at frequency v/3
(ii) The maximum intensity of the emitted radiation will occur at frequency 3v.
(iii) The total energy of emitted radiation will become 81 E
(iv) The total energy of emitted radiation will become 27 E
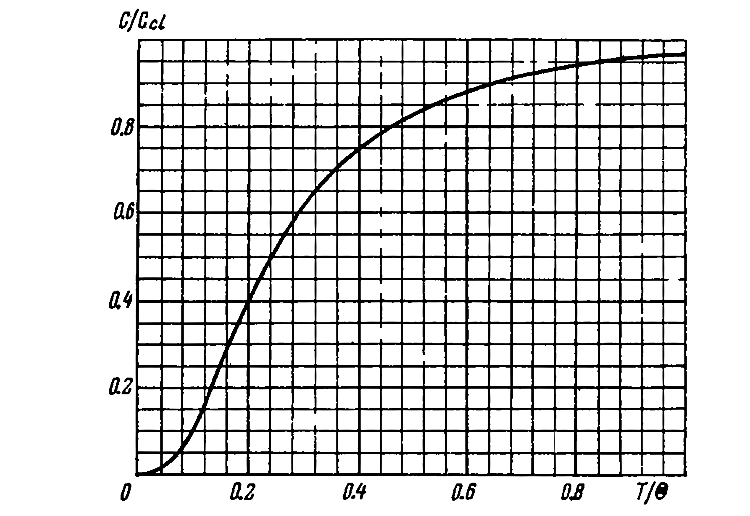
View SolutionFigure. 6.10 shows heat capacity of a crystal vs temperatue in terms of the Debye theory. Here Ccl is classical heat capacity Θ is the Debye temperature. Using this plot, find:
(a0 The Debye temperature for silver if at a temperature T=65K its molar heat capacity is equal to 15J(mol.K),
(b) the molar heat capacity of aluminum at T=80K if at T=250K it is equal to 22.4J(mol.K)
(c )the maximum vibration frequency for copper whose heat capacity at T=125K differs form the classical value by 25%.
View SolutionOne mole of a Van der Waals gas which had initially the volume V1 and the temperature T1 was transferred to the state with the volume V2 and the temperature T2. Find the corresponding entropy increment of the gas, assuming its molar heat capacity CV to be known.
View SolutionIn some process the temperature of a substance depends on its entropy S as T=aSn, where a and n are constants. Find the corresponding heat capacity C of the substance as a function of S. At what condition is C<0 ?
View SolutionA perfectly black body emits radiation at temperature T1K. If is to radiate at 16 times this power, its temperature T2K should be
View Solution
