A stationary ball of radius R is irradiated by a parallel stream of particles whose radius is r. Assuming the collision of a particle and the ball to be elastic find:
(a) the deflection angle θ of a particel as a function of its aiming parameter b:
(b) The fraction of a particles which after a collision with the ball are scattered into the angular interval between θ and θ+dthη:
(c )the probability of a particle to be deflected, after a collision with the ball, into the front hemisphere (θ<π2)
It is implied that the ball is too heavy to recoil.
(a) The trajectroy of the particle is symmertical about the radius vector through the point of impact. It is clear from the diagram that
θ=π−2φorφ=π2−θ2.
Also b=(R+r)sinφ=(R+r)cosθ2.
(b) With b defined above, the fraction of particle scattered between θ and θ+dθ(or the probability of the same) is
dP=|2πbdb|π(R+r)2=12sinθdθ
(c ) This is
P=∫π/2012sinθdθ=12∫0−1d(−cosθ)=12

Topper's Solved these Questions
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - ATOMIC AND NUCLEAR PHYSICSEXERCISE - Wave Properties Of Particle48videos
ATOMIC AND NUCLEAR PHYSICS
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - ATOMIC AND NUCLEAR PHYSICSEXERCISE - Properties Of Atom69videos
ATOMIC AND NUCLEAR PHYSICS
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - DIRECT CURRENTEXERCISE - All Questions15videos
DIRECT CURRENT
Similar Questions
A particle of mass m strikes another particle of same at rest. Find the angle between velocities of particles after the collision , if the collision is elastic.
View SolutionIn the previous problem , if the collision is head - on elastic , find (a) the velocities of balls immediately after the collision and (b) the maximum height attained by eacl ball.
View Solution
Knowledge Check
- Question 1 - Select One or More
In an elastic collision between smooth balls :
AThe kinetic energy remain constantBThe linear momentum remains constantCThe final kinetic energy is equal to the initial kinetic energyDThe final linear momentum is equal to the initial linear momentum - Question 2 - Select One
Velocity of the ball A after collision with the ball B as shown in the figure is (Assume perfectly inelastic and head - on collision)
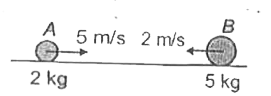 A37m/sB57m/sC17m/sDZero
A37m/sB57m/sC17m/sDZero - Question 3 - Select One or More
In an elastic collision between two particles
Anet external force is zeroBthe kinetic energy of the system before collision is equal to the kinetic of the system after collision.Clinear momentum of system before collision = linear momentum after collisionDthe total energy of the system is never conserved.
A ball of mass m makes an elastic collision with another identical ball at rest. Show that if the collision is oblique, the bodies go at right angles to each other after collision.
View Solution
A ball of mass m and radius r rolls along a circular path of radius R its speed at the bottom (θ=0∘) of the path is v0 find the force of the path on the ball as a function of θ.View SolutionStationary particles of mass m2 is hit by another particles of mass m1. The stationary particle deviates through θ and the other by 90∘. Find the value of θ if the collision is perfectly elastic.
View SolutionIn an elastic collision between two particles
View SolutionThe ball is released when the string is horizontal. The collision between the ball and the block is head - on elastic. The velocities of the ball and the block immediately after collision
 View Solution
View Solution

