Calculate the magnetic field induction at the centre of a hydrogen atom caused by an electron moving along the first Bohrorbit.
The revolving is electron is equivalent to a circular current
I=eT=e2πr/v=ev2πr
The magnetic induction
B=μ0I2r=μ0ev4πr2=μ04π.e.e2(4πε0)ħ.[me2ħ2(4πε0)]2
=μ0m2e7256π4ε30ħ5
Substitution gives B=12.56T ar the centre.
(In Gaussian units B=m2e7cħ5=125.6kG.)
Topper's Solved these Questions
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - ATOMIC AND NUCLEAR PHYSICSEXERCISE - Wave Properties Of Particle48videos
ATOMIC AND NUCLEAR PHYSICS
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - ATOMIC AND NUCLEAR PHYSICSEXERCISE - Properties Of Atom69videos
ATOMIC AND NUCLEAR PHYSICS
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - DIRECT CURRENTEXERCISE - All Questions15videos
DIRECT CURRENT
Similar Questions
Calcualte the value of X if magnetic field strength at the centre of a hydrogen atom caused by an electron moving along the first Bohr orbits is x2T.
View SolutionThe magnetic fieold at the centre of a hydrogen atom due to the motion of the electron in the first Bohr orbit is B . The magnetic field at the centre due to the motion of the electron in the second Bohr orbit will be B2xFind value of x.
View Solution
Knowledge Check
- Question 1 - Select One
The magnetic field induction produced at the centre of orbit due to an electron revolving in nth orbit of hydrogen atom is proportional to
An−3Bn−5Cn5Dn3
Magnetic field induction at the centre of a circular coil shown in the figure is
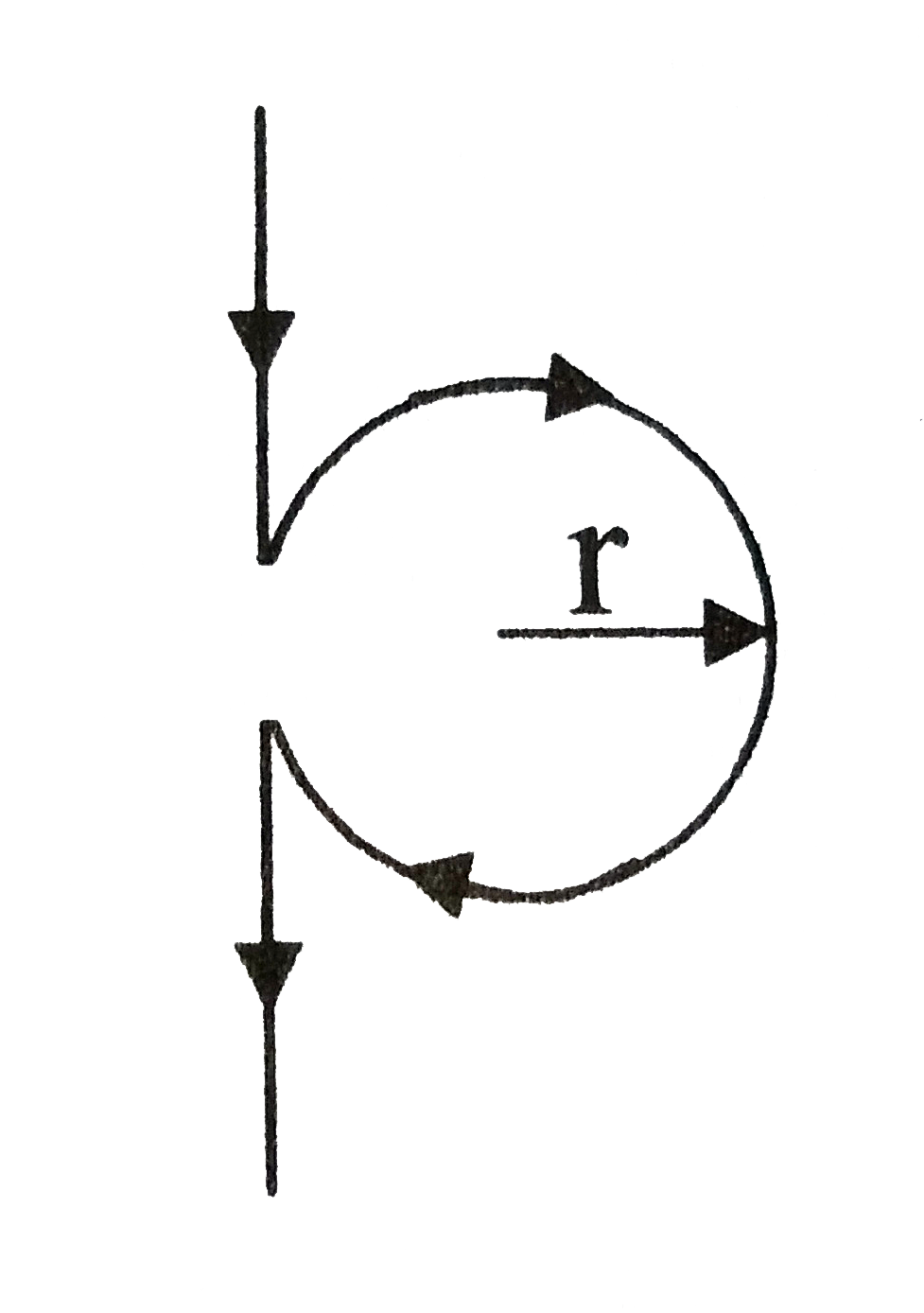 View Solution
View SolutionCalculate the magnetic field induction at the centre of a square shaped coil of side 10 cm, if it carries of current of 1A.
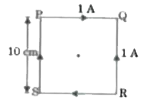 View Solution
View SolutionFind an expression fot the magneitc dipole moment and magnetic field induction at the centre of Bohr'r hypothetical hydrogen atom in the n th orbit of the electron in terms of universal constant.
View SolutionCalculate the energy of the electron in the ground state of the hydrogen atom.
View SolutionDeduce the expression for the magnetic field induction at the centre of a circular electron orbit of radius r, and angular velocity of orbiting electron ω.
View SolutionCalculate the velocity of an electron in the first Bohr orbit of a hydrogen atom
View SolutionCalculate the energy of an electron in the first Bohr orbit of hydrogen.
View Solution

