Rarefield Hg gas whose atoms are practically all in the ground state was lighted by a mercury lamp emitting a resonanace line of wavelength λ=253.65nm. As a result, the radiation power of Hg gas at that wavelength turned out to be P=35mW. Find the number of the atom in the state of resonance exitation whose mean lifetime is τ=0.15μs.
As a result of the lighting by mercury lamp a number of atoms are pumped to the excited state. In equilibrium the number of such atoms is N. Since the mean life time of the atom is T, the number decaying per unit is Nτ. Since a photon of energy 2πħcλ results from each decay, the total radiated power will be 2πħcλ.Nτ. This must equal P. Thus
N=Pτ/2πħcλ=Pτλ2πħ=6.7×109
Topper's Solved these Questions
- ATOMIC AND NUCLEAR PHYSICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - ATOMIC AND NUCLEAR PHYSICSEXERCISE - Molecules And Crystals
48 Videos
- ATOMIC AND NUCLEAR PHYSICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - ATOMIC AND NUCLEAR PHYSICSEXERCISE - Radioactivity
35 Videos
- ATOMIC AND NUCLEAR PHYSICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - ATOMIC AND NUCLEAR PHYSICSEXERCISE - Wave Properties Of Particle
48 Videos
- DIRECT CURRENTBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - DIRECT CURRENTEXERCISE - All Questions
15 Videos
Similar Questions
How many hydrogen atoms in the ground state are exited by means of monochromatic radiation of wavelength 970.6 Ã…. How many different lines are possible in the resulting emission spectrum? Find the longest wavelength among these .
View SolutionAtomic lithium of concentration n=3.6.1016cm−3 is at a temperature T=1500K. In this case the power emmitted at the resonat line's wavelength λ=671nm(2P→2S) per unit volume of gas is equal to P=0.30W/cm3. Find the mean lifetime of Li atoms in the resonance excitation state.
View Solution
Knowledge Check
Read the following text and answer the following questions on the basis of the same:
Atomic Absorption Spectrometer: The atomic absorption (AA) spectrometer is used to analyze metals at very low concentrations, typically in the parts per million (ppm) or parts per billion (ppb) ranges. A liquid sample containing dissolved material whose concentration is to be measured is aspirated into a thin, wide AA flame, or is introduced into a small carbon furnace which is heated to a high temperature.
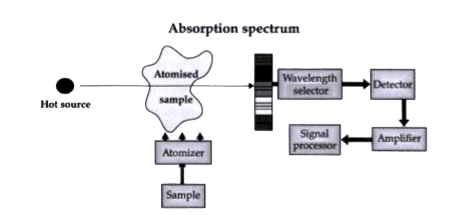
Basic Principle of AAS is the measurement of absorption of radiation by free atoms. The total amount of absorption depends on the number of free atoms present and the degreee to which the free atoms absorb the radiation. At the high temperature of the AA flame, the sample is broken down into atoms using an atomizer and it is the concentration of these atoms that is measured. Sample in the form of solution is used. It is broken up into a fine mist with the help of an atomizer. When the mist reaches the flame, the intense heat breaks up the sample into its individual atoms. When a photon coming out from the hot source hits an atom and the energy of the photon is equal to the gap between two electron energy levels of the atom, then the electron in the lower energy level absorb the photon and jumps up to the higher energy level. If the photon energy does not correspond to the difference between two energy levels, then the photon will not be absorbed (it may be scattered away). Hence in the spectrum, the wavelength corresponding to the absorbed photons is observed as black lines as shown in the following spectrum of Hydrogen. The dark lines correspon to the frequencies of light those have been absorbed by the sample element. Using this process, a source of photons (generally a white light) of various energies is used to obtain the absorption spectra of different materials and to identify them.
How the sample for analysis is deriven to atomic state in AAS?AAt a very high temperature, the sample is driven to its gaseous stateBUsing an atomizer and then intense heatingCBy rotating the solution of the sample at a very high speed.DNone of the above
The hydrogen atom in the ground state is excited by means of monochromatic radiation of wavelength xA0 The resulting spectrum consists of 15 different lines. Calculate the value of x.
View SolutionThe hydrogen atom in the ground state is excited by means of monochromatic radiation of wavelength xA0 The resulting spectrum consists of 15 different lines. Calculate the value of x.
View SolutionA gas of hydrogen atoms in its ground state, is excited by means of monochromatic radiation of wavelength 975A0. How many different spectral lines are possible in the resulting spectrum? (hc=12431.25eV−A0)
View SolutionThe wavelength of a resonat mercury line is λ==253.65nm. The mean life time of mercury atoms in the state of resonance excition is τ=.15μs. Evaluate the ration of the Doppler line broadening to the the natural linewidth at a gas temperature T=300K
View SolutionFind the ratio of the number of the atoms of gaseous sodium in the state 3P to that in the ground state 3S at a temperature T==2400K. The spectral line corresponding to the transition 3P→3S is known to have the wavelength λ=589nm.
View SolutionA parallel beam, of light of wavelength 100 nm passed through a sample of atomic hydrogen gas in ground state.
(a) Assume that when a phton supplies some of its energy to a hydrogen atom, the rest of the energy appears an another photon moving in the same direction as the incident photon. Neglecting the light emitted by the excited hydrogen atoms in the direction of the incident beam, what wavelengths may be observed in the transmitted beam?
(b) A radition detector is placed near the gas to detect radiation coming perpendicular to the incident beam. Find the wavelength of radiation that may be detected by the detector.
View SolutionA gas of identical hydrogen like atomos has some atoms in ground state and some atoms in a particular exceited state and dthere are no atoms in any other energy level. The atoms of the gas make transition to a higher energy stte by absrobing monochromatic light of wavelenght 304 ∘A. Subsequencly, the atoms emit radiation of only six different photon energies. Some of emitted photons have wavelenght 304∘A, some wavelength more and some have less that 304overeset(∘)A (Take he=12420eV−∘A)
Find the principal quantum number of the initially excicted state.
View Solution
