Derive the formula expressing molar heat capacity of a unidimensional crystal, a chain of identical atoms, as a function of temperature $T$ if the Debye temperature of the chain is equal ot $Θ$ . Simplyfie the octained expression for the case $T > Θ$

Text Solution

Verified by Experts

In the Debye approximation the number of modes per unit frequency interval is given by
$d N = \frac{1}{π v} d ω 0 \leq ω \leq \frac{k Θ}{ħ}$
But $\frac{k Θ}{ħ} = π n_{0} v$
Thus $d N = \frac{l}{π v} d ω, 0 \leq ω \leq π n_{0} v$
The enrgy per mode is
$< E \geq \frac{1}{2} ħ ω + \frac{ħ ω}{e^{ħ ω / k T} - 1}$
The total interval energy of the chain is
$U = \frac{l}{π v} \int_{0}^{π n_{0} v} \frac{1}{2} ħ ω d ω$
$+ \frac{l}{π v} \int_{0}^{π n_{0} v} \frac{ħ ω}{e^{ħ ω / k T} - 1} d ω = \frac{l ħ}{4 π v} {(π n_{0} v)}_{0}^{2} + \frac{l ħ}{4 π v} {(π n_{0} v)}_{0}^{2} + \frac{l}{π v ħ} {(k T)}^{2} \int_{0}^{Θ / T} \frac{x d x}{e^{x} - 1} = {ln}_{0} k . \frac{ħ}{k} (π n_{0} v) . \frac{1}{4}$
$+ {ln}_{0} k \frac{T^{2}}{(π n_{0} v ħ / k)} \int_{0}^{Θ / T} \frac{x d x}{e^{x} - 1}$
We put ${ln}_{0} k = R$ for $1$ mole of the chain
Then $U = R Θ {\frac{1}{4} + {(\frac{I}{Θ})}^{2} \int_{0}^{Θ / T} \frac{x d x}{e^{x} - 1}}$
Hence the molar heat capacity is by defferentiation
$C_{v} = (\frac{\partial U}{\partial T}) = R [2 (\frac{T}{Θ}) \int_{0}^{Θ / T} \frac{x d x}{e^{x} - 1} - \frac{Θ / T}{e^{e / T} - 1}]$
when $T > > Θ, C_{v} \approx R$

Updated on:21/07/2023

Class 12 PHYSICS ATOMIC PHYSICS

Topper's Solved these Questions

Knowledge Check

Question 1 - Select One
Two moles of an ideal mono-atomic gas undergoes a thermodynamic process in which the molar heat capacity $' C'$ of the gas depends on absolute temperature as $C = \frac{R T}{T_{0}}$ , where $R$ is gas consant and $T_{0}$ is the initial temperature of the gas. ( $V_{0}$ is the initial of the gas). Then answer the following questions:
The equation of process is
A $\frac{1}{P} = \frac{V_{0} T_{0}^{3 / 2}}{4 R T^{\frac{5}{2}}} e^{(T - \frac{T_{0}}{T_{0}})}$
B $\frac{1}{P} = \frac{V_{0} T_{0}^{3 / 2}}{2 R T^{\frac{5}{2}}} e^{(T - \frac{T_{0}}{T_{0}})}$
C $\frac{1}{P} = \frac{V_{0} T_{0}^{3 / 2}}{4 R T^{\frac{5}{2}}} e^{(T + \frac{T_{0}}{T_{0}})}$
D $\frac{1}{P} = \frac{V_{0} T_{0}^{3 / 2}}{3 R T^{\frac{5}{2}}} e^{(T - \frac{T_{0}}{T_{0}})}$
Question 2 - Select One
Two moles of an ideal mono-atomic gas undergoes a thermodynamic process in which the molar heat capacity $' C'$ of the gas depends on absolute temperature as $C = \frac{R T}{T_{0}}$ , where $R$ is gas consant and $T_{0}$ is the initial temperature of the gas. ( $V_{0}$ is the initial of the gas). Then answer the following questions:
The minimum volume of gas is
A ${(\frac{2}{3})}^{3 / 2} V_{0} e^{1 / 2}$
B ${(\frac{4}{3})}^{3 / 2} V_{0} e^{1 / 2}$
C ${(\frac{5}{3})}^{3 / 2} V_{0} e^{1 / 2}$
D ${(\frac{8}{3})}^{3 / 2} V_{0} e^{1 / 2}$
Question 3 - Select One
According to Dulong $&$ Petits law, molar heat capacity of solids at room temperature is nearly equal to 3R. This can be explained using law of equipartition. Each atom of solid is boned to neighboring atoms by interatomic forces. Each atom can vibrate about its equilibrium positum. So each atom has 6 degrees of freedom. But in relaity, the molar heat capacity of solids varies. with temperature as shown in figure.

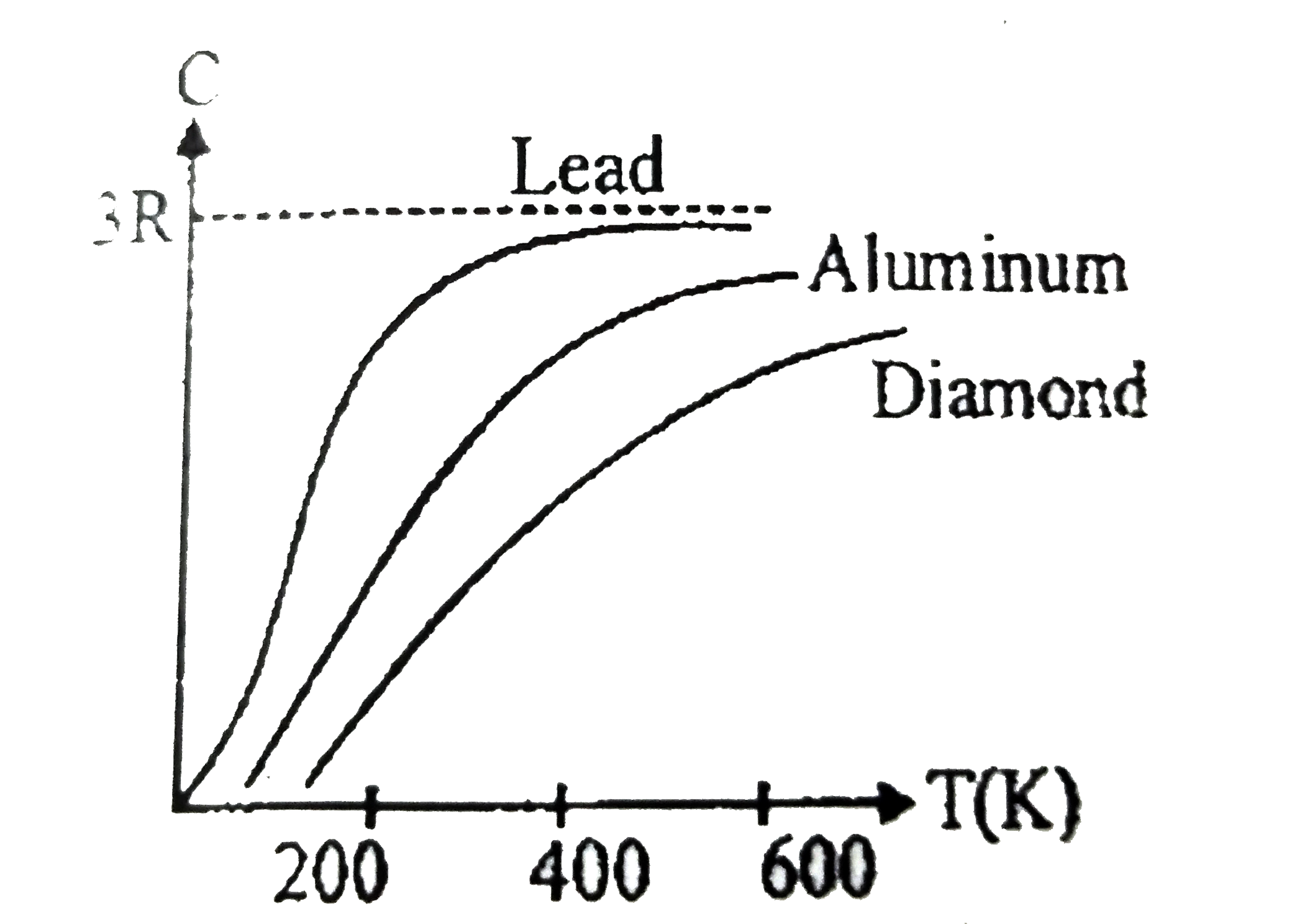
At low temperature, the heat capcities decrease with decreasing temperature. This is due to the fact that variational degrees of freedom are frozen out at low temperatures.
Selec the correct statement(s).
AA sample of lead requires less heat to go from 100K to 150K then to go from 300K to 350K
BA sample of lead requires more heat to go from 400K to 440K then to go from 100K to 140K
CFor diamond at room temperatures also vibrational degrees of freedom are partially frozen.
DThe specific heat capacity of all solids at high temperature is nearly the same.

IE IRODOV, LA SENA & SS KROTOV-ATOMIC AND NUCLEAR PHYSICS-Molecules And Crystals

Home
Ask Doubt
Profile

Derive the formula expressing molar heat capacity of a unidimensional crystal, a chain of identical atoms, as a function of temperature T if the Debye temperature of the chain is equal ot Θ. Simplyfie the octained expression for the case T>Θ

Topper's Solved these Questions

Similar Questions

Knowledge Check

IE IRODOV, LA SENA & SS KROTOV-ATOMIC AND NUCLEAR PHYSICS-Molecules And Crystals

Derive the formula expressing molar heat capacity of a unidimensional crystal, a chain of identical atoms, as a function of temperature $T$ if the Debye temperature of the chain is equal ot $Θ$ . Simplyfie the octained expression for the case $T > Θ$