: To divide a line segment in a given ratio.
To divide a line segment in a given ratio, follow these step-by-step instructions:
Step 1: Draw the Line Segment
- Draw a line segment AB of length 5 cm.
Step 2: Draw a Ray
- From point A, draw a ray AA' at any angle (not necessarily 90 degrees) to the line segment AB.
Step 3: Divide the Ray into Equal Parts
- Since the ratio given is 2:3, add the two parts of the ratio together (2 + 3 = 5).
- Use a compass to mark off equal segments on the ray AA'. Choose a convenient length for the compass and mark off 5 equal segments along the ray. Label these points as A1, A2, A3, A4, and A5.
Step 4: Join the Last Point to Point B
- Draw a line segment from point A5 to point B.
Step 5: Draw a Parallel Line
- Now, from point A2 on the ray, draw a line parallel to the line segment A5B. This parallel line will intersect the line segment AB at point P.
Step 6: Identify the Division Point
- The point P where the parallel line intersects AB is the point that divides the line segment AB in the ratio 2:3.
Conclusion
- You have successfully divided the line segment AB in the ratio 2:3.
---
- Draw a line segment AB of length 5 cm.
Step 2: Draw a Ray
- From point A, draw a ray AA' at any angle (not necessarily 90 degrees) to the line segment AB.
- Since the ratio given is 2:3, add the two parts of the ratio together (2 + 3 = 5).
- Use a compass to mark off equal segments on the ray AA'. Choose a convenient length for the compass and mark off 5 equal segments along the ray. Label these points as A1, A2, A3, A4, and A5.
- Draw a line segment from point A5 to point B.
- Now, from point A2 on the ray, draw a line parallel to the line segment A5B. This parallel line will intersect the line segment AB at point P.
- The point P where the parallel line intersects AB is the point that divides the line segment AB in the ratio 2:3.
- You have successfully divided the line segment AB in the ratio 2:3.
Topper's Solved these Questions
- BOOK - NCERTCHAPTER - CONSTRUCTIONSEXERCISE - Example2videos
CONSTRUCTIONS
- BOOK - NCERTCHAPTER - CONSTRUCTIONSEXERCISE - EXERCISE 11.17videos
CONSTRUCTIONS
- BOOK - NCERTCHAPTER - CIRCLESEXERCISE - SOLVED EXAMPLES3videos
CIRCLES
- BOOK - NCERTCHAPTER - COORDINATE GEOMETRYEXERCISE - EXERCISE 7.35videos
COORDINATE GEOMETRY
Similar Questions
Knowledge Check
- Question 1 - Select One
If the extremities of a line segment of length l moves in two fixed perpendicular straight lines, then the locus of the point which divides this line segment in the ratio 1 : 2 is-
Aa parabolaBan ellipseCa hyperbolaDNone of these - Question 2 - Select One
A point R (h, k) divides a line segment between the axis in the ratio 1 : 2 what will be the equation on line
Axh−2yk=4Bxh+2yk=3Cxk+yh=1Dx2k+yh=1
By geometrical construction, it is possible to divide a line segment in the ratio √3:1√3.
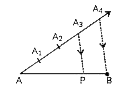
View SolutionFill in the blanks/tables with suitable information:
In the given figure, P divides the line segment AB in the ratio ____________
 View Solution
View SolutionIn the given figure, ABCD is a parallelogram. AE divides the line segment BD in the ratio 1 : 2. If BE = 1.5 cm find BC.
 View Solution
View SolutionDivide a line segment AB in the ratio 3:7, What is the minimum number of points marked on a ray AX at equal distances?
View SolutionDetermine a point which divides a line segment 7 cm long, internally in the ratio 2:3
View SolutionFind the point P divides the line segment joining the points (-1,2) and (4,-5) in the ratio 3:2
View Solution

