If →a,→b,→c are the position vectors of points A, B, C and D respectively such that (→a−→d)⋅(→b−→c)=(→b−→d)⋅(→c−→a)=0, then D is the
Step by step video & image solution for If veca,vec b, vecc are the position vectors of points A, B, C and D respectively such that (veca -vecd)* (vecb-vecc) =(vecb-vecd) *(vecc -veca) =0, then D is the by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Similar Questions
A, B C and D are four points in a plane with position vectors, →a,→b→cand→d respectively, such that (→a−→d).(→b−→c)=(→b−→d).(→c−→a)=0 then point D is the ______ of triangle ABC.
View SolutionA, B C and D are four points in a plane with position vectors, →a,→b→cand→d respectively, such that (→a−→d).(→b−→c)=(→b−→d).(→c−→a)=0 then point D is the ______ of triangle ABC.
View Solution
Knowledge Check
A, B, C and D have position vectors →a,→b,→cand→d, repectively, such that →a−→b=2(→d−→c). Then
AAB and CD bisect each otherBBD and AC bisect each otherCAB and CD trisect each otherDBD and AC trisect each other
A, B, C and D have position vectors →a,→b,→cand→d, repectively, such that →a−→b=2(→d−→c). Then
View SolutionIf →a,→b,→c,→d are the position vectors of points A,B,CandD, respectively referred to the same origin O such that no three of these points are collinear and →a+→c=→b+→d, then prove that quadrilateral ABCD is a parallelogram.
View SolutionIf →a,→b,→c,→d are the position vectors of points A,B,CandD, respectively referred to the same origin O such that no three of these points are collinear and →a+→c=→b+→d, then prove that quadrilateral ABCD is a parallelogram.
View SolutionIf →a,→b,→c,→d are the position vectors of the verticles of a cyclic quadrilateral ABCd prove that
∣∣→a×→b+→b×→d+→d×→a∣∣(→b−→a).(→d−→a)+∣∣→b×→c+→c×→d+→d×→b∣∣(→b−→c).(→d−→c)=0
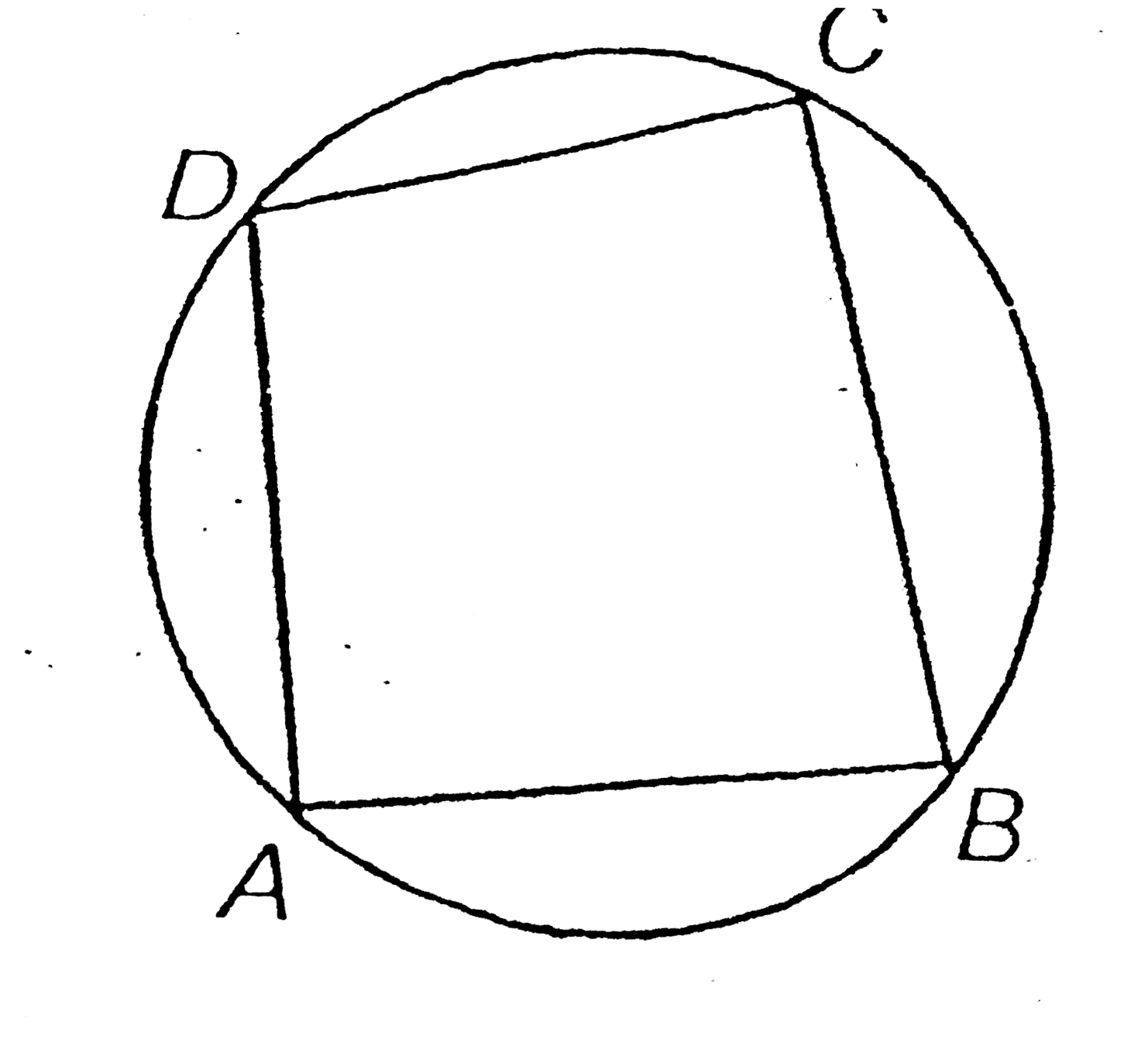
View SolutionIf →a,→b,→c,→d are the position vectors of the verticles of a cyclic quadrilateral ABCd prove that
∣∣→a×→b+→b×→d+→d×→a∣∣(→b−→a).(→d−→a)+∣∣→b×→c+→c×→d+→d×→b∣∣(→b−→c).(→d−→c)=0

View SolutionIf →a,→b,→cand→d are the position vectors of the vertices of a cycle quadrilateral ABCD, prove that ∣∣→a×→b+→b×→d+→d×→a∣∣(→b−→a).(→d−→a)+∣∣→b×→c+→c×→d+→d+→d×→b∣∣(→b−→c).(→d−→c)
View SolutionIf →a,→b,→cand→d are the position vectors of the vertices of a cycle quadrilateral ABCD, prove that ∣∣→a×→b+→b×→d+→d×→a∣∣(→b−→a).(→d−→a)+∣∣→b×→c+→c×→d+→d+→d×→b∣∣(→b−→c).(→d−→c)
View Solution
