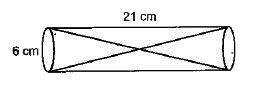
Two solid cones A and B are placed in a cylindrical tube as shown in the figure The ratio of their capacities is 2:1 Find the heights and capacities of cones Also find the volume of the remaining portion of the cylinder. 21 cm

Video Solution

Text Solution

Verified by Experts

$\frac{V_{1}}{V_{2}} = \frac{2}{1} = \frac{\frac{1}{3} π r^{2} h_{1}}{\frac{1}{3} π r^{2} h_{2}}$
$\frac{h_{1}}{h_{2}} = 2$
$h_{1} = 2 h_{2}$
$h_{1} + h_{2} = 21$
$2 h_{2} + h_{2} = 21$
$h_{2} = 7$
$h_{1} = 14 c m$
$V_{1} = \frac{1}{3} \cdot \frac{22}{7} \cdot 9 \cdot 14 = 132 c m^{3}$
$V_{2} = \frac{1}{3} \cdot \frac{22}{7} \cdot 9 \cdot 7 = 66 c m^{3}$
Volume of cylinder= $\frac{22}{7} \cdot 9 \cdot 21 = 594 c m^{3}$
Volume of rim= $594 - 132 - 66 = 396 c m^{3}$ .

The radius of the base of a cone is 21 cm and the height is 20 cm. Find the volume the cone
A $8460 c m^{3}$
B $9240 c m^{3}$
C $4620 c m^{3}$
D $3230 c m^{3}$
From a solid cylinder of height 10 cm and radius of the base 6 cm, a cone of same height and same base is removed. The volume of the remaining solid is :
A $240 π$ cu. cm
B5280 cu. cm
C $620 π$ cu. cm
D $360 π$ cu. cm