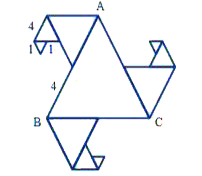
In Fig. all triangle are equilateral and AB = 8 units.Other triangles have been formed by taking the mid points of the sides. What is the perimeter of the figure
Step by step video & image solution for In Fig. all triangle are equilateral and AB = 8 units.Other triangles have been formed by taking the mid points of the sides. What is the perimeter of the figure by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Similar Questions
In Fig. 6.15 all triangles are equilateral and AB =8 units. Other triangles have been formed by taking the mid points of the sides. What is the perimeter of the figure?
View SolutionLet ABC be a triangle of area 24sq.units and PQR be the triangle formed by the mid-points of the sides triangle ABC. Then what is the area of triangle PQR.
View Solution
Knowledge Check
An equilateral triangle is drawn by joining the midpoints of the sides of another equilateral triangle. A third equilateral triangle is drawn inside the second one joining the midpoints of the sides of the second equilateral tringle, and the process continues infinitely. Find the sum of the perimeters of all the equilateral triangles, if the side of the largest equilateral triangle is 24 units.
A288 unitsB72 unitsC36 unitsD144 unitsA new triangle is formed by joining the mid-points of an equilateral triangle. Again a new triangle is formed by using the mid-points of this triangle, this process goes on till infinity. If the side of the big equilateral triangle is 24 units, find the total perimeter of such triangle formed ?
A288B72C36D144
Consider an equilateral triangle of a side of unit length. A new equilateral triangle is formed by joining the mid-points of the first one, then a third equilateral triangle is formed by joining the mid-points of the second. The process is continued. The sum perimeter of all triangles thus formed is
View SolutionOne side of an equilateral triangle is 36 cm. The mid-points of its sides are joined to form another triangle. Again another triangle is formed by joining the mid-points of the sides of this triangle and the process is continued indefinitely. Determine the sum of areas of all such triangles including the given triangle.
View SolutionProve that the four triangles formed by joining in pairs, the mid-points of three sides of a triangle, are congruent to each other.
View SolutionProve that the four triangles formed by joining in pairs, the mid-points of three sides of a triangle, are congruent to each other.
View SolutionThe base of an equilateral triangle with side 2a lies along the y-axis such that the mid point of the base is at the origin. Find the vertices of the triangle.
View SolutionA side of an equilarteral triangle is 20 cm long .A second equilateral triangle is inscribed in it by joning the mid -point of the sides of the first triangle . The process is caontinued as shown in the accompanying diagram . find the perimeter of the sixth inscribed equilateral triangle .
View Solution
