Chords equidistant from the center of a circle are equal in length.
OX=OY
In∠OAXand∠ODY
OA=OD(radii)
OX=OY(given)
∠OXA−∠OYD(900)
∠OAXand∠ODY
AX=DY
AB=CD=PQ
so, chords are equal.
Similar Questions
Knowledge Check
r : Two chords of a circle are equidistant from the centre if and only if they are equal in length
Statements r can be interpreted asAIf two polygons are congruent then they are equal in shape and sizeBIf two polygons are equal in shape and size then· they' are not congruentCBoth (1) & (2)DNoen of these
Chords of a circle which are equidistant from the centre are equal.
View SolutionWrite the following statements in conditional form, "chords, which are equidistant from the centers of congruent circles, are congruent."
View SolutionChord AB is 6 inches from the center of the circle and is 10 inches long. Draw another chord CD that is equidistant from the center of the circle. How long is chord CD?
View SolutionProve that the chords inclined on the same angle to the radius or diameter of a circle are equal in length.
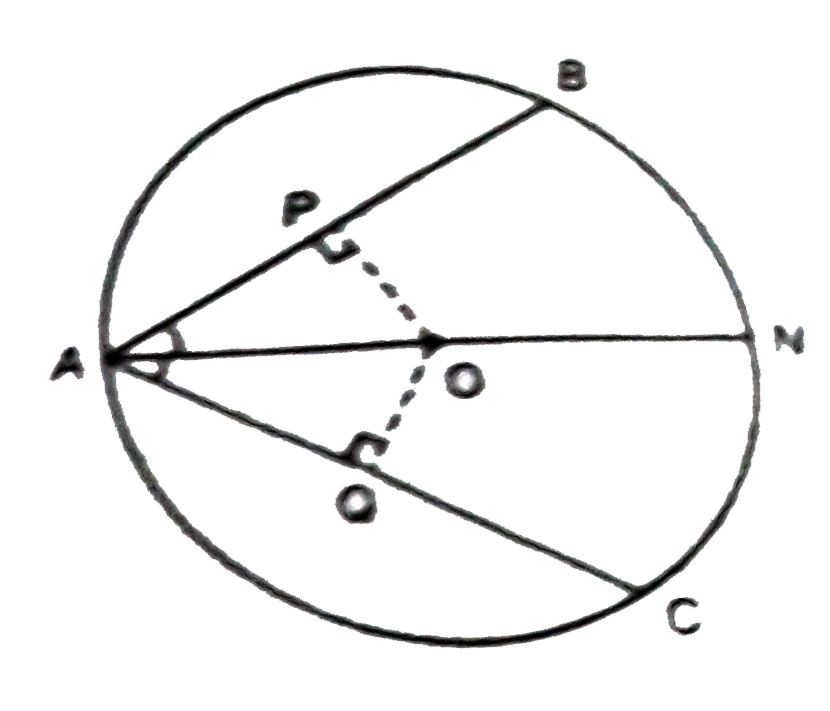
View SolutionProve that the chords inclined on the same angle to the radius or diameter of a circle are equal in length.

View SolutionChords of congruent circles which are equidistant from the corresponding centres, are equal.
View SolutionProve Chords of congruent circles which are equidistant from the corresponding centres, are equal.
View Solution