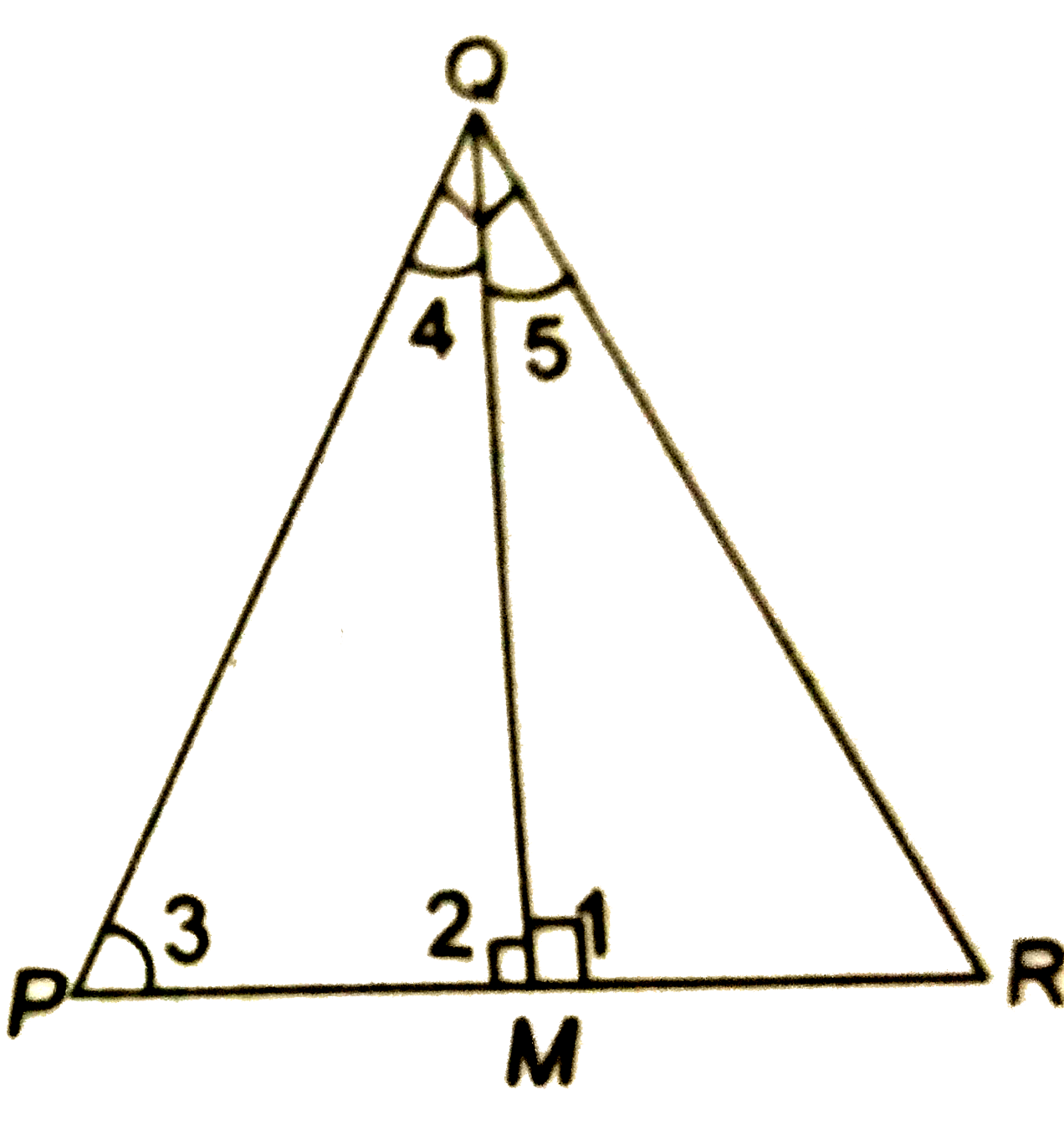
ΔPQR में , QM⊥PR और PR2−PQ2=QR2 है सिद्ध कीजिये कि QM2=PM×MR
∴ PR2−PQ2=QR2
⇒ PR2=PQ2+QR2
⇒ ∠4+∠5=90∘ (पाइथागोरस प्रमेय के विलोम से)
अब ∴ ∠2=90∘
⇒ ∠3+∠4=90∘ (कोण-योग गुण) ...(1)
परन्तु ∠4+∠5=90∘ (ऊपर सिद्ध किया है) ...(2)
∴ (1) और (2) से
∠3+∠4=∠4+∠5
⇒ ∠3=∠5
अब ΔPMQ और ΔQMR में
∠2=∠1 (प्रत्येक 90∘)
∠3=∠5 (अभी सिद्ध किया है )
∴ ΔPMQ~ΔQMR (AA उपप्रमेय)
⇒ QM2=PM×MR) यही सिद्ध करना था
Topper's Solved these Questions
- त्रिभुज BOOK - NOOTAN HINDICHAPTER - त्रिभुज EXERCISE - प्रश्नावली 6A
24 Videos
- त्रिभुज BOOK - NOOTAN HINDICHAPTER - त्रिभुज EXERCISE - प्रश्नावली 6B
26 Videos
- त्रिकोणमिति के कुछ अनुप्रयोग BOOK - NOOTAN HINDICHAPTER - त्रिकोणमिति के कुछ अनुप्रयोग EXERCISE - विविध प्रश्नावली (दीर्घ उतरिये प्रश्न)
6 Videos
- दो चर वाले रैखिक समीकरण युग्म BOOK - NOOTAN HINDICHAPTER - दो चर वाले रैखिक समीकरण युग्म EXERCISE - विविध प्रश्नावली (बहुविकल्पीय प्रश्न)
7 Videos
Similar Questions
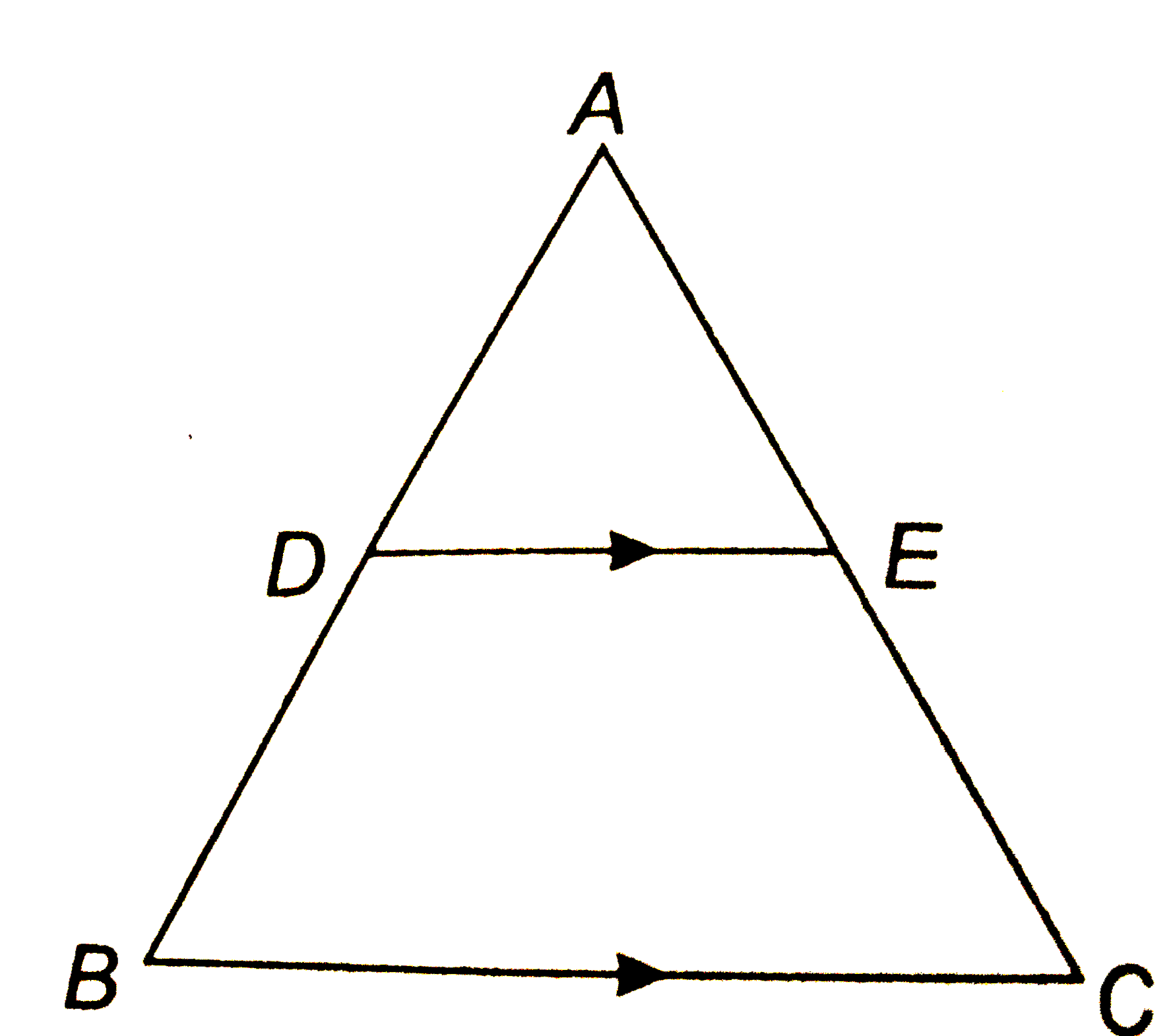
संलग्न चित्र में , बिन्दु D , AB को 3:5 में विभाजित करता है ज्ञात कीजिये
(i) AEEC (ii) ADAB (iii) AEAC
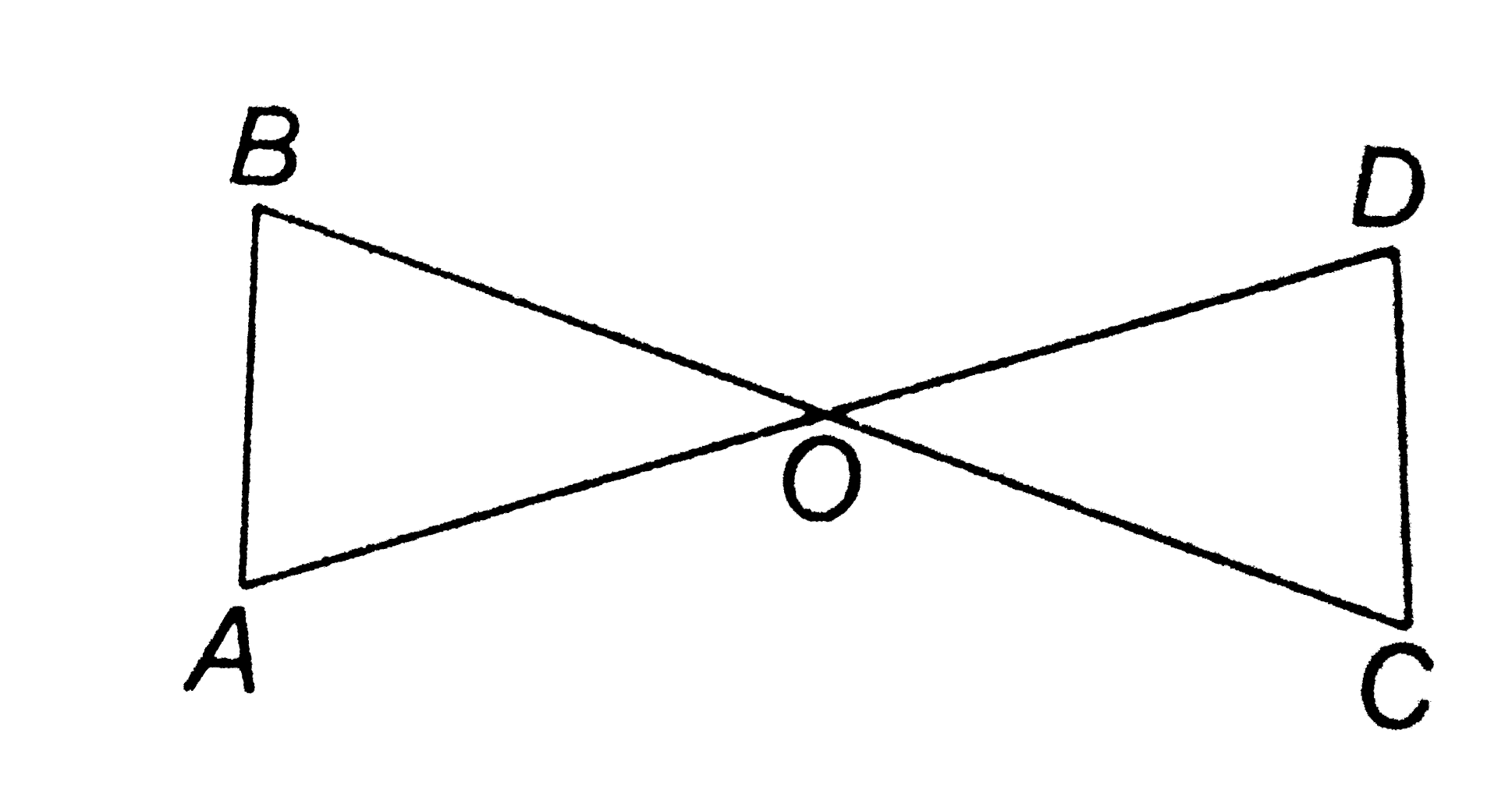
View Solutionदिए चित्र में यदि, AB||CD तो सिद्ध कीजिये कि ΔAOB~ΔDOC
View Solutionकिसी सीधी क्षैतिज सड़क के ऊपर एक हवाई जहाज क्रमागत किलोमीटर के दो पत्थरों के बीच उड़ रहा है। ये पत्थर हवाई जहाज के दोनों ओर स्थित हैं। हवाई जहाज से पत्थरों के अवनतांश 30∘ और 60∘ हैं। सड़क से वायुयान की ऊँचाई मीटर में ज्ञात कीजिए।
View Solutionसमीकरण 5x−15y=16 और 3x−9y=485 के युग्म का के हल होंगे :
View SolutionIn PQR, QM⊥PR and PR2−PQ2=QR2 . Prove that QM2=PM×MR
View Solutionpq+qr−pr−r2
View SolutionIn ΔPQR, seg PM is median. PM=9, PQ2+PR2=290 then find length of seg QR.
View SolutionIn ΔPQR, PQ2=PR2+QR2 then state which angle will be the right angle.
View Solutionयदि ΔPQR में, QM⊥PR तथा PR2−PQ2=QR2 हो तो सिद्ध करो की QM2=PM×MR
View Solutionसिद्ध कीजिये की बिंदु (1,−2),(3,6),(5,10) और (3,2) एक समांतर चतुर्भुज के शीर्ष है ।
View Solutionरिक्त स्थानों को भरे।
ΔPQR में PQ=QR,औरPR2=2PQ2 तो ∠Q=……
View SolutionIn an isosceles ΔPQR,PR=QR and PQ2=2PR2, then ∠R=
View Solutionसिद्ध कीजिये कि अंतराल (−1,1) में फलन f(x)=x2−x+1 न तो वर्धमान है और न ही हस्यमान है।
View Solutionसिद्ध कीजिये कि (0,2π) में फलन f(x)=x−sinx वर्धमान है।
View Solutionसिद्ध कीजिये कि3−2√5 एक अपरिमेय संख्या है।
View Solution
