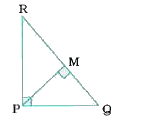
यदि ΔPQR में, QM⊥PR तथा PR2−PQ2=QR2 हो तो सिद्ध करो की QM2=PM×MR
ΔPQR में दिया है कि
PR2−PQ2=QR2
∴PR2=PQ2+QR2
⇒ΔPQR एक समकोण त्रिभुज है जिसका कोण Q समकोण है |
⇒∠2+∠3=90∘

साथ ही ∠1+∠2=90∘ [∵∠PMQ=90∘]
∴∠1=∠3
इसी प्रकार हम यह प्राप्त करते है कि
∠2=∠4
अतः ΔPMQ और ΔQMR में
∠1=∠3 तथा ∠2=∠4
∴ समरूपता की AA कसौटी से
ΔPMQ~ΔQMR
⇒PMQM=MQMR
⇒QM2=PM×MR
Topper's Solved these Questions
- त्रिभुजेंBOOK - RD SHARMACHAPTER - त्रिभुजेंEXERCISE - प्रश्नावली 4.1
12 Videos
- त्रिभुजेंBOOK - RD SHARMACHAPTER - त्रिभुजेंEXERCISE - प्रश्नावली 4.2
20 Videos
- त्रिकोणमितीय सर्वसमिकाएँ BOOK - RD SHARMACHAPTER - त्रिकोणमितीय सर्वसमिकाएँ EXERCISE - बहु विकल्पीय प्रश्न
28 Videos
- दो चार वाले रैखिक समीकरण युग्म BOOK - RD SHARMACHAPTER - दो चार वाले रैखिक समीकरण युग्म EXERCISE - बहु विकल्पीय प्रश्न
16 Videos
Similar Questions
कोष्ठक में दिए हुए शब्दों में से ही शब्दों को चुनकर रिक्त स्थान को भारिये:
सभी वृत.......(सर्वांगसम, समरूप) होते है|
View Solutionत्रिभुज ABC की भुजाओं AB और AC बिंदु D और E इस प्रकार है की DE भुजा BC के समानांतर है| यदि|||
AD=6 सेमि , DB = 9 सेमि तथा AE =8 सेमि, हो तो AC ज्ञात करो|
View Solutionयदि secθ+tanθ=x हो तो secθ=
View Solutionनिम्न समीकरण युग्म का अद्वितीय हल होंगे, यदि
kx−y=2
6x−2y=3
View SolutionIn ΔPQR, D is the mid-point of ¯¯¯¯¯¯QR.then¯¯¯¯¯¯¯PM is ___________,PD is___________. Is QM=MR?
View SolutionA circle is inscribed in a triangle PQR with PQ = 10 cm, QR = 8 cm and PR = 12 cm. Find the lengths QM, RN and PL.
View SolutionIn PQR, QM⊥PR and PR2−PQ2=QR2 . Prove that QM2=PM×MR
View Solutionयह दिया है कि LM=MN,QM=MR,ML⊥PQतथा MN⊥PR, तो सिध्द करो कि PQ=PR.
View SolutionΔPQR में , QM⊥PR और PR2−PQ2=QR2 है सिद्ध कीजिये कि QM2=PM×MR
View SolutionPQR is a triangle right angled at P and M is a point on QR such that PM⊥QR . Show that PM2=QM.MR.
View SolutionPQR is a triangle right angled at P and M is a point on QR such that PM ⊥ QR . Show that PM2=QM.MR .
View SolutionIn ΔPQR,∠PQR=90∘,segQM⊥hypPR,PM=16andRM=9thenQM…….
View SolutionPQR is a triangle right angled at P and M is a point on QR such that PM ⊥ QR . Show that PM2 = QM .MR.
View SolutionPQR is a triangle right angled at P and M is a point on QR such that PM ⊥ QR . Show that PM2 = QM .MR.
View SolutionPQR is a Deltaright angled at P and M is a point on QR such that PM⊥QR. Show that PM2=QM⋅MR.
View Solution
