ΔABC में, O एक आन्तरिक बिन्दु है। सिद्ध कीजिए कि : AB+BC+CA<2(OA+OB+OC)
Step by step video & image solution for DeltaABC में, O एक आन्तरिक बिन्दु है। सिद्ध कीजिए कि : AB+BC+CAlt2(OA+OB+OC) by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
- त्रिभुज BOOK - NOOTAN HINDICHAPTER - त्रिभुज EXERCISE - विविधि प्रश्नावली (लघु उत्तरीय प्रश्न )
10 Videos
- चतुर्भुजBOOK - NOOTAN HINDICHAPTER - चतुर्भुजEXERCISE - विविध प्रश्नावली
24 Videos
- दो चरों वाले रैखिक समीकरण BOOK - NOOTAN HINDICHAPTER - दो चरों वाले रैखिक समीकरण EXERCISE - विविध प्रश्नावली
12 Videos
Similar Questions
∠ABC में कोई बिन्दु P इस प्रकार है कि P से AB और BC पर डाले गये लम्ब बराबर है। सिद्ध कीजिए कि BP,∠ABC को समद्विभाजित करता है।
View Solutionएक चतुर्भुज के तीन कोण 100∘,98∘,92∘ है। चौथा कोण ज्ञात कीजिए।
View Solutionx अक्ष का समीकरण लिखिय|
View Solution'O' is any point in the interior of a Delta ABC prove that AB+BC+CA>OA+OB+OC
View SolutionLet O be any point in the interior of ΔABC, prove that :
AB+BC+CA<2(OA+OB+OC)
View Solutionif D,E and F are the mid-points of the sides BC,CA and AB respectively of the ΔABCandO be any points, then prove that OA+OB+OC=OD+OE+OF
View Solutionत्रिभुज ABC के अन्तः भाग में O कोई बिन्दु है | सिध्द करो कि
AB+BC+CA<2(OA+OB+OC)
View Solutionत्रिभुज ABC के अन्तः भाग में O कोई बिन्दु है | सिध्द करो कि
OA+OB+OC>12(AB+BC+CA)
View SolutionABCDE एक समपंचभुज है। O इसका केंद्र है। सिद्ध कीजिए कि −−→OA+−−→OB+−−→OC+−−→OD+−−→OE=→0
View Solutionयदि ¯¯¯¯¯¯OA=¯a,¯¯¯¯¯¯OB=¯b तथा C,AB पर एक ऐसा बिंदु है कि ¯¯¯¯¯¯AC=3¯¯¯¯¯¯AB तो सदिश ¯¯¯¯¯¯OC बराबर है:
View Solutionसिद्ध कीजिए कि f(x)=ax,o<a<1,R में ह्रासमान है।
View Solutionसिद्ध कीजिए कि बिन्दु (2,0),(11,6) तथा (−4,−4) समरेख है।
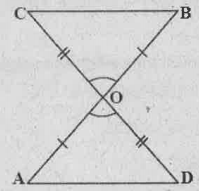
View Solutionఇచ్చిన పటంలో AB మరియు CD లు 'O' వద్ద ఖండించుకొనుచున్నాయి. OA=OB మరియు OD=OC అయిన AD∣∣BC అని నిరూపించండి.
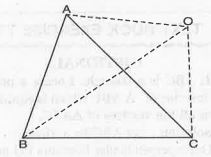
View SolutionO is any point in the exterior of a ΔABC. Prove that 2(OA+OB+OC)>(AB+BC+CA)
 .
.
View SolutionThe point O is outside the ∠ABC. Show that 2(OA+OB+OC)>AB+BC+CA.
View Solution
