दी आकृति में, ABC एक समबाहु त्रिभुज है, PQ∣∣AC और AC को R तक इस प्रकार बढ़ाया गया है कि CR = BP है। सिद्ध कीजिए कि QR, PC को समद्विभाजित करती है।
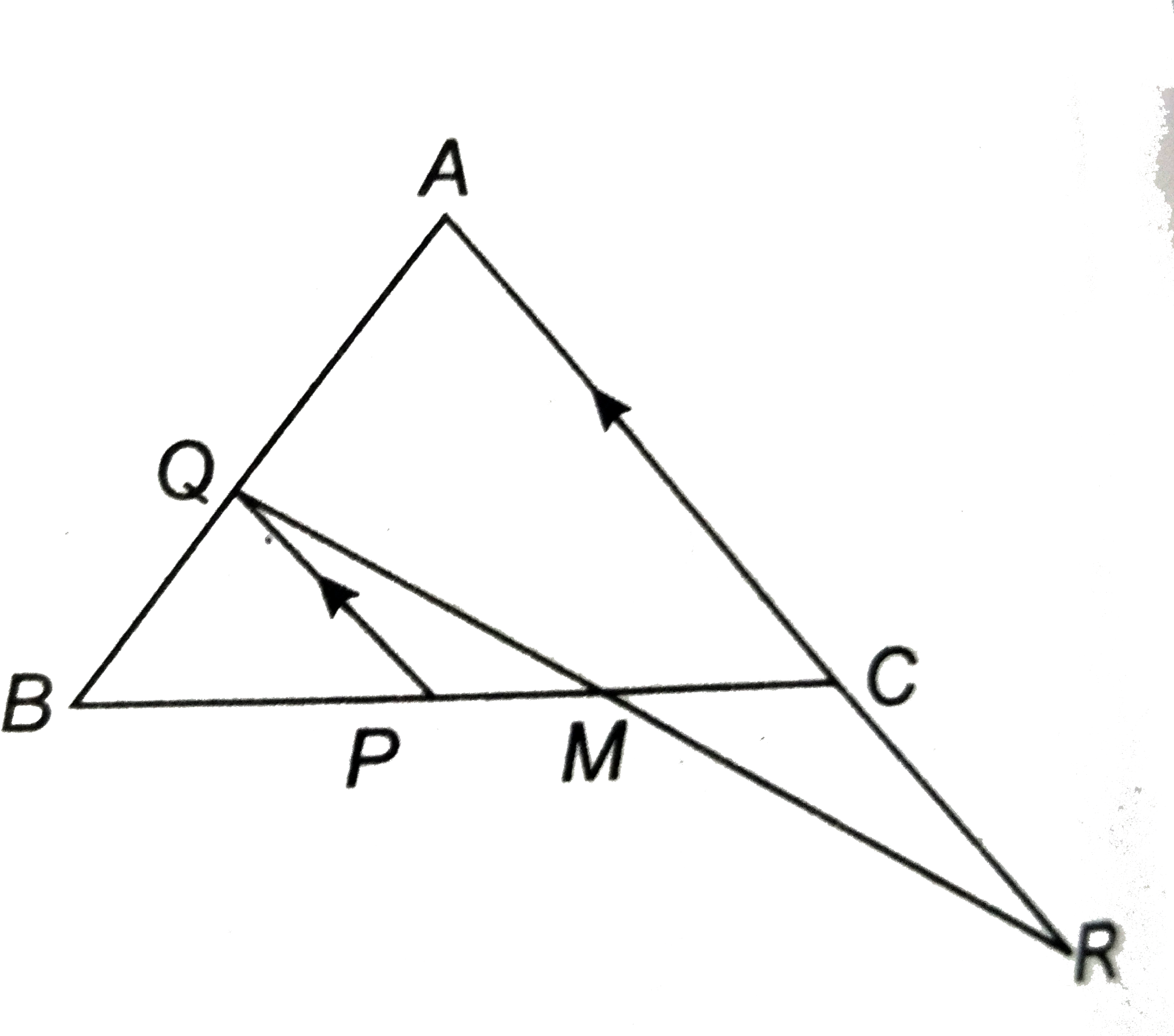
Step by step video & image solution for दी आकृति में, ABC एक समबाहु त्रिभुज है, PQ||AC और AC को R तक इस प्रकार बढ़ाया गया है कि CR = BP है। सिद्ध कीजिए कि QR, PC को समद्विभाजित करती है। by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
- त्रिभुज BOOK - NOOTAN HINDICHAPTER - त्रिभुज EXERCISE - विविधि प्रश्नावली (लघु उत्तरीय प्रश्न )
10 Videos
- चतुर्भुजBOOK - NOOTAN HINDICHAPTER - चतुर्भुजEXERCISE - विविध प्रश्नावली
24 Videos
- दो चरों वाले रैखिक समीकरण BOOK - NOOTAN HINDICHAPTER - दो चरों वाले रैखिक समीकरण EXERCISE - विविध प्रश्नावली
12 Videos
Similar Questions
∠ABC में कोई बिन्दु P इस प्रकार है कि P से AB और BC पर डाले गये लम्ब बराबर है। सिद्ध कीजिए कि BP,∠ABC को समद्विभाजित करता है।
View Solutionएक चतुर्भुज के तीन कोण 100∘,98∘,92∘ है। चौथा कोण ज्ञात कीजिए।
View Solutionx अक्ष का समीकरण लिखिय|
View SolutionDetermine the point of symmetry of a regular hexagon.
View SolutionMatch the following Column A to Column B

View SolutionMatch the following Column A to Column B

View SolutionMatch the following Column A to Column B

View SolutionThe inequation represented by the graph given below is :
View SolutionThe inequation that best describes the graph given below is _________
View SolutionThe inequation that best describes the following graph is _________
View Solutionवह सबसे बड़ी संख्या ज्ञात कीजिए जो 247 और 2055 को इस प्रकार विभाजित करती है कि प्र्त्येक स्थिति में शेषफल 7 प्राप्त हो।
View Solutionएक ही आधार BC पर तीन समद्विबाहु त्रिभुज △PBC ,△QBC और △RBC स्तिथ है। सिद्ध कीजिए कि P ,Q और R समरेख है।
View Solutionसिद्ध कीजिए कि सम्मिश्र संख्याओं 0, 2i और √3+i को निरूपित करने वाले बिंदु समबाहु त्रिभुज के शीर्ष है।
View Solutionकिसी त्रिभुज ABC में A(a,0)औरB(−a,0) बिंदु है । शीर्ष C इस प्रकार गमन करता है कि tanA+tanB=2 . बिंदु C का बिन्दुपथ ज्ञात कीजिए ।
View Solutionयदि f:R→R इस प्रकार है कि f(x) = |x|, तो सिद्ध कीजिए कि fof = f .
View Solutionएक समतल निर्देशांकों अक्षों को A,B,C पर इस प्रकार मिलता है कि त्रिभुज ABC का केंद्रक (1,2,3) है तो समतल का समीकरण होगा
View Solution
