यदि E, F, G और H क्रमशः समान्तर चतुर्भुज ABCD की भुजाओं के मध्य-बिन्दु है, तो दर्शाइए कि ar(EFGH)=12ar(ABCD)
दिया है, E, F, G और H क्रमशः AB, BC, CD और AD के मध्य-बिन्दु है। EF, FG, GH और HE को मिलाया। अब HE || DC || AB है।
अब समान्तर चतुर्भुज HDCE और ΔHGE समान आधार HF और समान समान्तर रेखाओं DC और HF के मध्य स्थित है।
∴ar(ΔHGF)=12ar(HDCF) ...(1)
इसी प्रकार समान्तर चतुर्भुज ABFH और ΔHEF समान आधार HF और समान समान्तर रेखाओं HF और AB के मध्य स्थित है।

ar(ΔHEF)=12ar(ABFH) ...(2)
समीकरण (1) और (2) को जोड़ने पर
⇒ar(ΔHGF)+ar(ΔHEF)=12[ar(HDCF)+ar(ABFH)]
ar(EFGH)=12ar(ABCD)
Topper's Solved these Questions
- समान्तर चतुर्भुजों और त्रिभुजों के क्षेत्रफल BOOK - NOOTAN HINDICHAPTER - समान्तर चतुर्भुजों और त्रिभुजों के क्षेत्रफल EXERCISE - प्रश्नावली 9.3
16 Videos
- समान्तर चतुर्भुजों और त्रिभुजों के क्षेत्रफल BOOK - NOOTAN HINDICHAPTER - समान्तर चतुर्भुजों और त्रिभुजों के क्षेत्रफल EXERCISE - प्रश्नावली 9.4
8 Videos
- समान्तर चतुर्भुजों और त्रिभुजों के क्षेत्रफल BOOK - NOOTAN HINDICHAPTER - समान्तर चतुर्भुजों और त्रिभुजों के क्षेत्रफल EXERCISE - प्रश्नावली 9.1
1 Videos
- चतुर्भुजBOOK - NOOTAN HINDICHAPTER - चतुर्भुजEXERCISE - विविध प्रश्नावली
24 Videos
Similar Questions
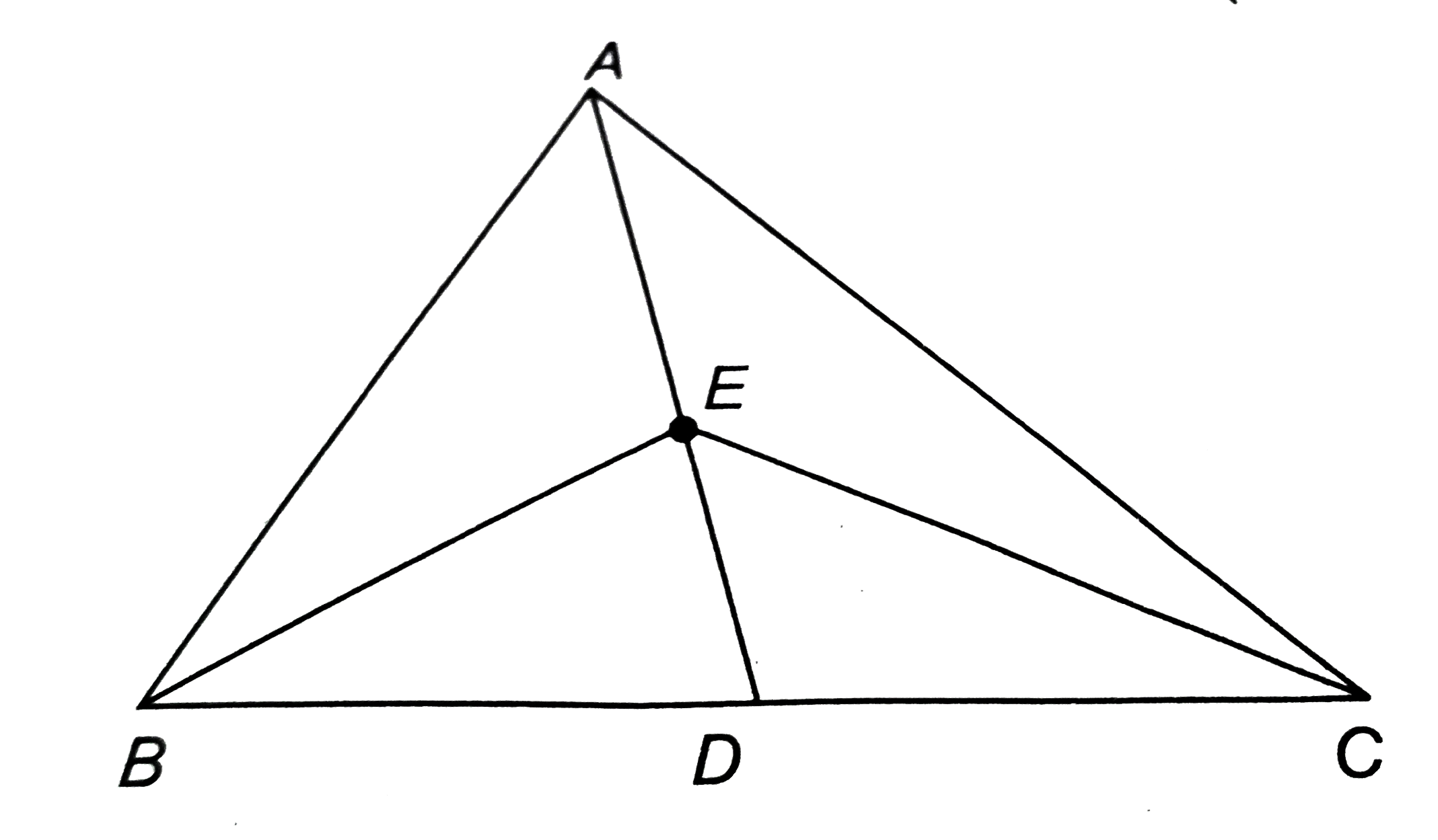
आकृति में, ΔABC की एक माध्यिका AD पर स्थित E कोई बिन्दु है। दर्शाइए कि ar(ΔABE)=ar(ΔACE) है।
View Solutionसमान्तर चतुर्भुज ABCD और आयत ABEF एक ही आधार पर स्थित है और उनके क्षेत्रफल बराबर है। दर्शाइए कि समान्तर चतुर्भुज का परिमाप आयत के परिमाप आयत के परिमाप से अधिक है।
View Solutionनिम्नलिखित आकृतियों में से कौन-सी आकृतियाँ एक ही आधार और एक ही समान्तर रेखाओं के बीच स्थित है? ऐसी स्थिति में, उभयनिष्ठ आधार और दोनों समान्तर रेखाएँ लिखिए।
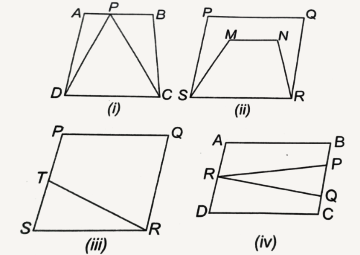
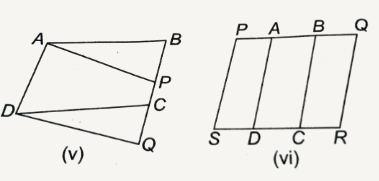
View Solutionएक चतुर्भुज के तीन कोण 100∘,98∘,92∘ है। चौथा कोण ज्ञात कीजिए।
View SolutionIf E,F,G and H are respectively the mid-points of the sides of a parallelogram ABCD, show that ar(EFGH)=12ar(ABCD).
View SolutionIf E, F, G and H are respectively the mid-points of the sides of a parallelogram ABCD, Show that ar(EFGH)=12AR (ABCD)
View Solutionयदि E,F,G और H क्रमश : समांतर चतुर्भुज ABCD कि भुजाओ के मध्य - बिंदु है, तो दर्शाइए कि ar(EFGH)=12ar(ABCD) है।
View Solutionयदि E, F, G और H क्रमशः समांतर चतुर्भुज ABCD की भुजाओ के मध्य-बिन्दु है, तो दर्शाइए कि (EFGH) 12 ar (ABCD) है।
View Solutionयदि ABCD एक समांतर चतुर्भुज है, तो सिद्ध कीजिए कि
ar(ΔABD)=ar(ΔBCD)=ar(ΔABC)=ar(ΔACD)=12ar(||gmABCD)
View SolutionIf E,F, G and H are respectively the mid-points of the sides of a parallelogram ABCD, show that ar (EFGH) = 12 ar (ABCD)
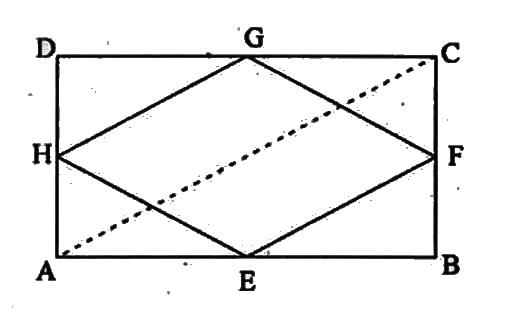
View SolutionΔABC की भुजाओं के मध्यबिंदु D,E,F हैं। यदि O कोई बिंदु हो तो दर्शाइए कि
¯¯¯¯¯¯OE+¯¯¯¯¯¯OF+¯¯¯¯¯¯DO=¯¯¯¯¯¯OA
View Solutionयदि किसी त्रिभुज की भुजाओं के मध्य - बिंदुओं के निर्देशांक (2,1),(−1,−3) और (4,5) हों , तो उसके शीर्षों के निर्देशांक ज्ञात कीजिए ।
View SolutionIf E, F G and H are respectively the midpoints of the sides AB, BC, CD and AD of a parallelogram ABCD, show that ar(EFGH) =12 ar (ABCD) .
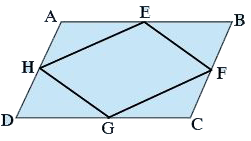
View SolutionIf E, F G and H are respectively the midpoints of the sides AB, BC, CD and AD of a parallelogram ABCD, show that ar(EFGH) =12 ar (ABCD) .
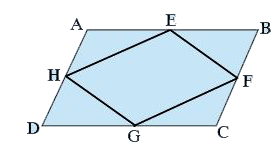
View SolutionIf E, F G and H are respectively the midpoints of the sides AB, BC, CD and AD of a parallelogram ABCD, show that ar(EFGH) =12 ar (ABCD) .
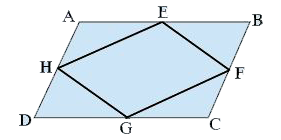
View Solution
