If E, F, G and H are respectively the mid-points of the sides of a parallelogram ABCD, show that ar(EFGH)=12ar(ABCD).
Step by step video & image solution for If E, F, G and H are respectively the mid-points of the sides of a parallelogram ABCD, show that ar(EFGH)=1/2ar(ABCD). by Maths experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Similar Questions
If E, F G and H are respectively the midpoints of the sides AB, BC, CD and AD of a parallelogram ABCD, show that ar(EFGH) =12 ar (ABCD) .
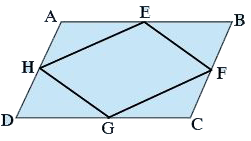
View SolutionIf E, F G and H are respectively the midpoints of the sides AB, BC, CD and AD of a parallelogram ABCD, show that ar(EFGH) =12 ar (ABCD) .
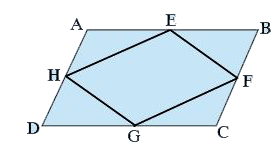
View SolutionIf E, F G and H are respectively the midpoints of the sides AB, BC, CD and AD of a parallelogram ABCD, show that ar(EFGH) =12 ar (ABCD) .
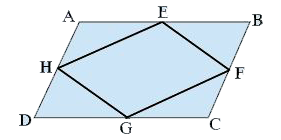
View SolutionIn figure, ABCD and EFGD are two parallelograms and G is the mid-point of side CD. Then, ar (DPC) = (1)/(2) ar(EFGD).
View SolutionIf E, F, G and H are the mid-points of sides of a parallelogram ABCD then ar (EFGH) = ............ .
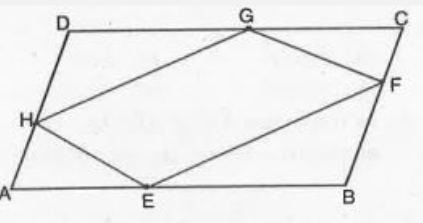
View Solutionਜੇਕਰ E,F,G ਅਤੇ H ਕ੍ਰਮਵਾਰ ਸਮਾਂਤਰ ਚਤੁਰਭੁਜ ABCD ਦੀਆਂ ਭੁਜਾਵਾਂ ਦੇ ਮੱਧ ਬਿੰਦੂ ਹੋਣ, ਤਾਂ ਦਰਸਾਉ ਕਿ ar(EFGH)=12ar(ABCD) ਹੈ।
View SolutionE, F, G and H are the mid-points of the sides of a parallelogram ABCD. Show that area of quadrilateral EFGH is half of the area of parallelogram ABCD.
View SolutionP और Q किसी समांतर चतुर्भुज ABCD की भुजाओं DC तथा AD पर स्थित दो बिंदु है |दिखाएँ की ar(ΔAPB)=ar(ΔBQC)
View Solution
