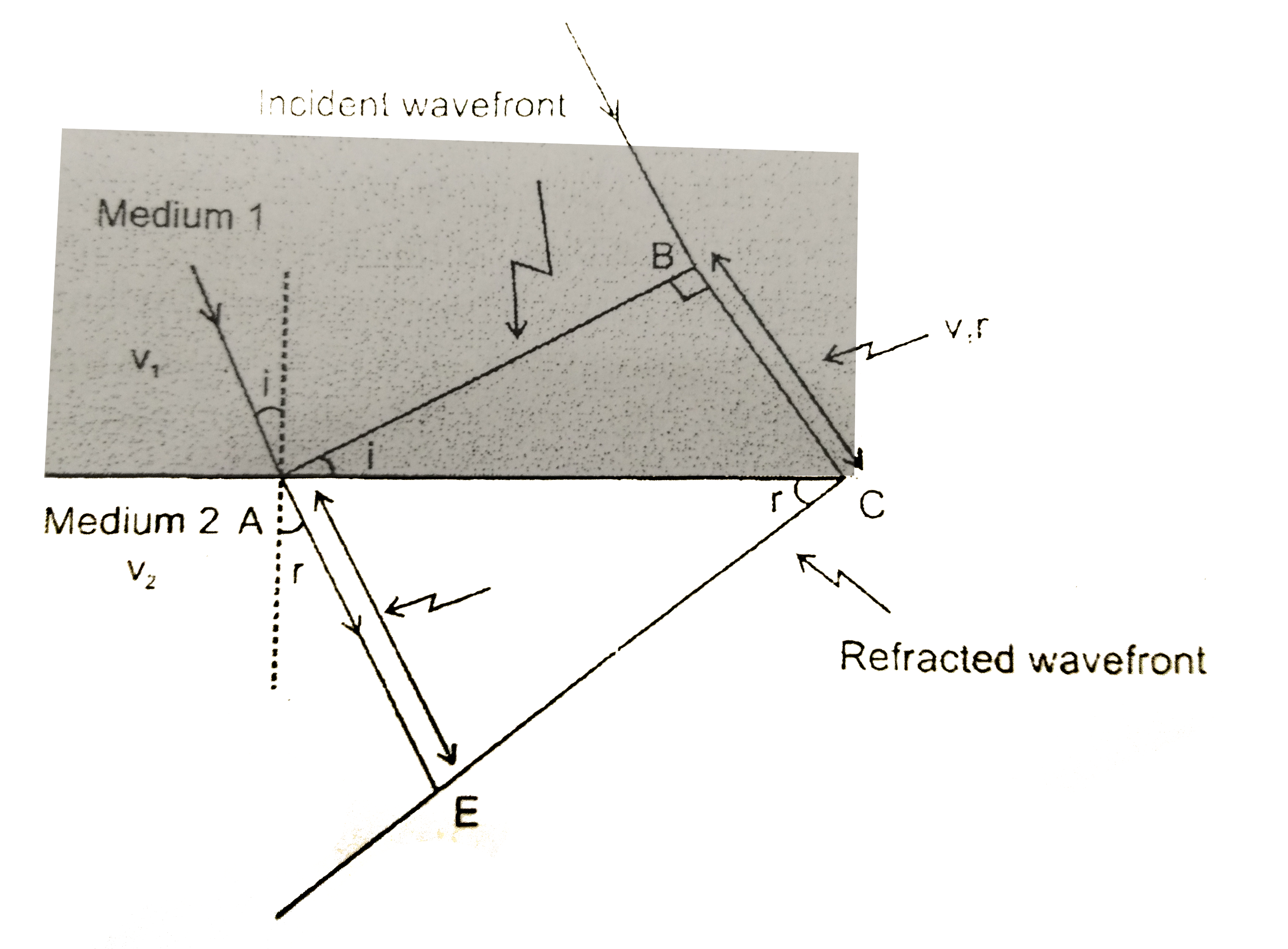
Two media of refractive indices μ1 and μ2(ν1>μ2) are separated by a plane surface. If some part of a plane wavefront is in first medium and other part of wavefront in the second medium show the shape of the wavefront in this position diagramatically.
AB and BC are two plane wavefronts inclined to each other

Topper's Solved these Questions
- LIGHT WAVE AND INTERFERENCE OF LIGHT BOOK - CHHAYA PUBLICATIONCHAPTER - LIGHT WAVE AND INTERFERENCE OF LIGHT EXERCISE - NCERT TEXTBOOK QUESTIONS WITH ANSWER HINT
13 Videos
- LIGHT WAVE AND INTERFERENCE OF LIGHT BOOK - CHHAYA PUBLICATIONCHAPTER - LIGHT WAVE AND INTERFERENCE OF LIGHT EXERCISE - NCERT EXEMPLAR QUESTIONS WITH ANSWER HINT
3 Videos
- LIGHT WAVE AND INTERFERENCE OF LIGHT BOOK - CHHAYA PUBLICATIONCHAPTER - LIGHT WAVE AND INTERFERENCE OF LIGHT EXERCISE - Section Related Questions
13 Videos
- KIRCHHOFF'S LAWS AND ELECTRICAL MEASUREMENT BOOK - CHHAYA PUBLICATIONCHAPTER - KIRCHHOFF'S LAWS AND ELECTRICAL MEASUREMENT EXERCISE - CBSE SCANNER
16 Videos
- Magnetic Properties of Materials BOOK - CHHAYA PUBLICATIONCHAPTER - Magnetic Properties of Materials EXERCISE - CBSE SCANNER
11 Videos
Similar Questions
A monochromatic light is incident on the plane interface AB between two media of refractive indices μ1 and (μ2>μ1) at an angle of incidence θ as shown in Fig.
The angle θ is infinitesimally greater than the critical angle for the two media so that total internal reflection takes place. Now, if a transparent slab DEFG of uniform thickness and of refractive index μ3 is introduced on the interface (as shown in the figure), show that for any value of μ3 all light will ultimately be reflected back into medium II.

View SolutionAn intially parallel cyclindrical beam travels in a medium of refractive index μ(I)=μ0+μ2I, where μ0 and μ2 are positive constants and I is intensity of light beam. The intensity of the beam is decreasing with increasing radius.
Answer the following questions :
The initial shape of the wavefront of the beam is
View Solution
Knowledge Check
Three transparent media of refractive indices μ1,μ2,μ(3) respectively, are stacked as shown. A ray of light follows the path shown. No light enters the third medium.

Then-Aμ1<μ2<μ3Bμ2<μ1<μ3Cμ1<μ3<μ2Dμ3<μ1<μ2An intially parallel cyclindrical beam travels in a medium of refractive index μ(I)=μ0+μ2I, where μ0 and μ2 are positive constants and I is intensity of light beam. The intensity of the beam is decreasing with increasing radius.
Answer the following questions :
The initial shape of the wavefront of the beam isAconcaveBconvex near the axis and concave near the peripheryCplanarDconvexThere are three optical media 1,2 and 3 with the refractive indices μ1>μ2>μ3.
(TIR → total internal reflection)Awhen a ray of light travels from 3 to 1 no TIR will placeBcritical angle between 1 and 2 is less than the critical angle between 1 and 3Ccritical angle between 1 and 2 is more than the critical angle between 1 and 3Dchances of TIR are move when ray of light travels from 1 to 3 as compared to the case when it travel from 1 to 2
The diagram, given below, shows the refracton of a plane wavefront, incident on the surface PP' separating two media, (1)and(2). Which of the media is the rarer one ?
View SolutionThe diagram, given below, shows the refracton of a plane wavefront, incident on the surface PP' separating two media, (1)and(2). Which of the media is the rarer one ?

View SolutionThere are three optical media 1,2 and 3 with the refractive indices μ1>μ2>μ3.
(TIR → total internal reflection)
View SolutionA spherical surface of radius R ssparates two media of refractive indices μ1 and μ1 as shown in figure., Where should an object be placed in medium 1 so that a real image is formed in medium 2 at the same distance?
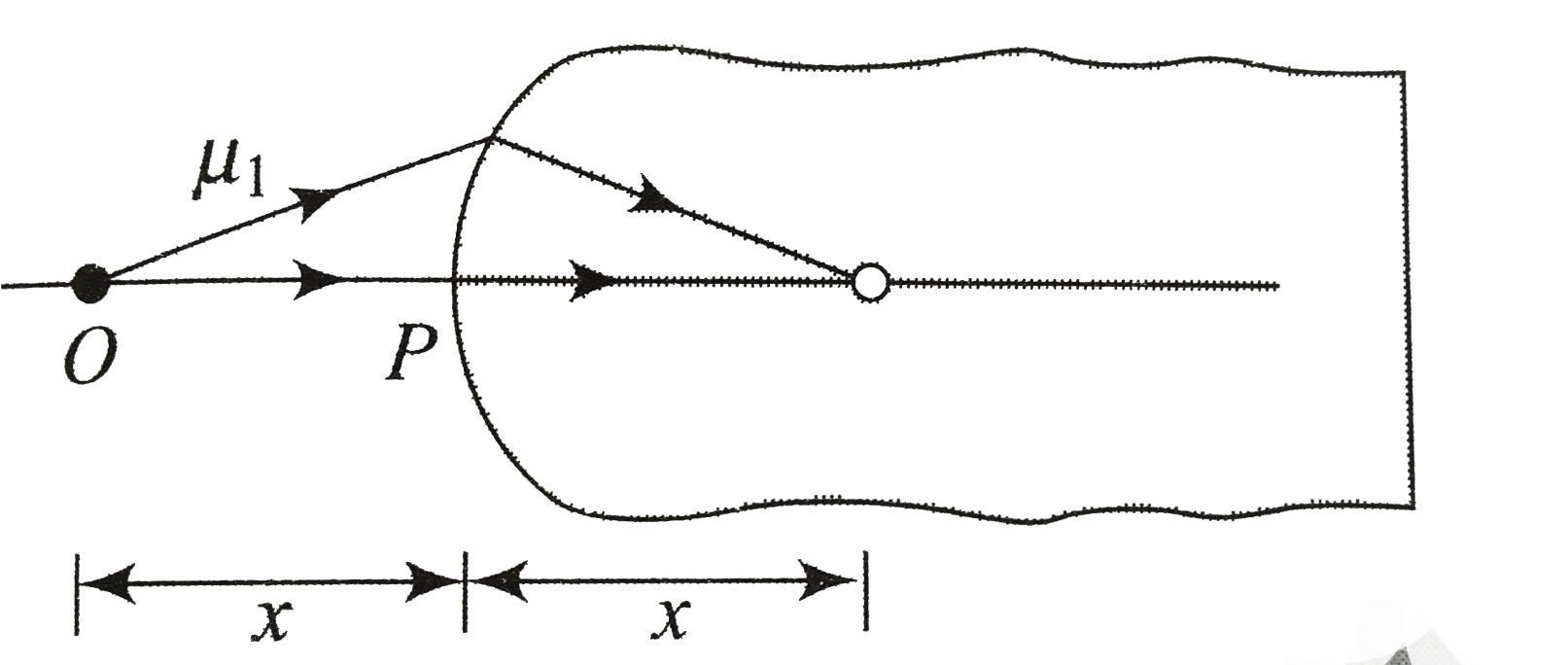
View SolutionA spherical surface of radius R ssparates two media of refractive indices μ1 and μ1 as shown in figure., Where should an object be placed in medium 1 so that a real image is formed in medium 2 at the same distance?

View Solution
