A rectangular block of mass 2 kg is to be held against a rough vertical wall by applying a force of 98 N perpendicular to the wall. What is the coefficients of friction if the applied force is the minimum required force?
0.1
0.15
0.2
0.3
The correct Answer is:C
To find the coefficient of friction (μ) for a rectangular block of mass 2 kg held against a rough vertical wall by an applied force of 98 N, we can follow these steps:
Step 1: Identify the forces acting on the block
- The weight (W) of the block acting downwards:
W=m⋅g=2kg⋅9.8m/s2=19.6N
- The applied force (F) acting perpendicular to the wall:
F=98N
- The normal force (R) exerted by the wall on the block, which is equal to the applied force when the applied force is the minimum required force to hold the block in place:
R=F=98N
- The frictional force (f_s) acting upwards to prevent the block from sliding down.
Step 2: Set up the equilibrium condition
For the block to be in equilibrium vertically, the frictional force must balance the weight of the block:
fs=W
Substituting the weight:
fs=19.6N
Step 3: Relate the frictional force to the normal force
The maximum static frictional force can be expressed in terms of the coefficient of friction (μ) and the normal force (R):
fs=μ⋅R
Substituting the values we have:
19.6N=μ⋅98N
Step 4: Solve for the coefficient of friction (μ)
Rearranging the equation to solve for μ:
μ=fsR=19.6N98N=0.2
Final Answer
The coefficient of friction (μ) is:
μ=0.2
- The weight (W) of the block acting downwards:
W=m⋅g=2kg⋅9.8m/s2=19.6N
- The applied force (F) acting perpendicular to the wall:
F=98N
- The normal force (R) exerted by the wall on the block, which is equal to the applied force when the applied force is the minimum required force to hold the block in place:
R=F=98N
- The frictional force (f_s) acting upwards to prevent the block from sliding down.
For the block to be in equilibrium vertically, the frictional force must balance the weight of the block:
fs=W
Substituting the weight:
fs=19.6N
The maximum static frictional force can be expressed in terms of the coefficient of friction (μ) and the normal force (R):
fs=μ⋅R
Substituting the values we have:
19.6N=μ⋅98N
Rearranging the equation to solve for μ:
μ=fsR=19.6N98N=0.2
The coefficient of friction (μ) is:
μ=0.2
Topper's Solved these Questions
- BOOK - MARVEL PUBLICATIONCHAPTER - FRICTIONAL IN SOLIDS AND LIQUIDS EXERCISE - TEST YOUR GRASP10videos
FRICTIONAL IN SOLIDS AND LIQUIDS
- BOOK - MARVEL PUBLICATIONCHAPTER - FORCE, WORK AND TORQUEEXERCISE - TEST YOUR GRASP10videos
FORCE, WORK AND TORQUE
- BOOK - MARVEL PUBLICATIONCHAPTER - MAGNETIC EFFECT OF ELECTRIC CURRENT EXERCISE - TEST YOUR GRASP10videos
MAGNETIC EFFECT OF ELECTRIC CURRENT
Similar Questions
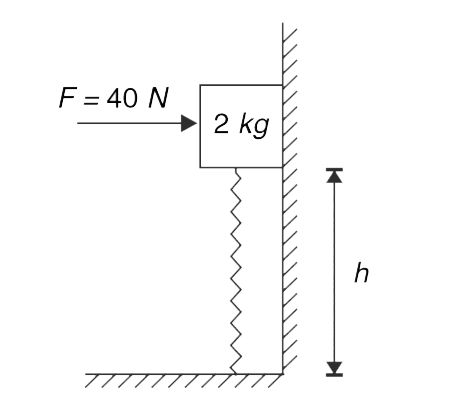
(i) In the arrangement shown in the figure the coefficient of friction between the 2 kg block and the vertical wall is μ=0.5. A constant horizontal force of 40 N keeps the block pressed against the wall. The spring has a natural length of 1.0 m and its force constant is k=400Nm–1. What should be the height h of the block above the horizontal floor for it to be in equilibrium. The spring is not tied to the block.
(ii) A block of mass M is pressed against a rough vertical wall by applying a force F making an angle of θ with horizontal (as shown in figure). Coefficient of friction between the wall and the block is μ=0.75.
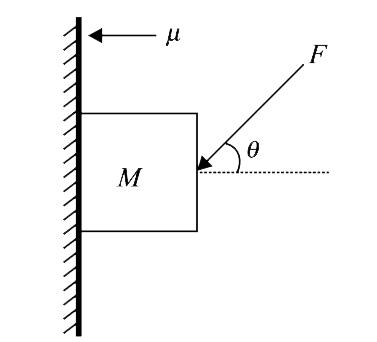
(a) If F = 2 Mg, find the range of values of θ so that the block does not slide
[Take tan37∘=0.75,sin24∘=0.4]
(b) Find the maximum value of θ above which equilibrium is not possible for any magnitude of force F.View SolutionA block of mass M is held against a rough vertical wall by pressing it with a finger . If the coefficient of friction between the block and the wall is μ and the acceleration due to gravity is g , calculate the minimum force required to be applied by the finger to hold the block against the wall.
View Solution
Knowledge Check
- Question 1 - Select One
A rectangular block of mass 6 kg is to be held against a rough vertical wall by appplying a force perpendicular to the wall. What is the minimum force to be applied, if the coefficient of friction is 0.42?
A140 NB120 NC100 ND80 N - Question 2 - Select One
A block of 1 kg is stopped against a wall by applying a force F perpendicular to the wall. If μ=0.2 then minimum value of F will be
A980 NB49 NC98 ND490 N - Question 3 - Select One or More
A block of mass 1 kg is held at rest against a rough vertical surface by pushing by a force F horizontally. The coefficient of friction is 0.5. When
 AF = 40 N, friction on the block is 20 N.BF = 30 N, friction on the block is 10 N.CC = 20 N, friction on the block is 10 N.DMinimum value of force F to keep block at rest is 20 N.
AF = 40 N, friction on the block is 20 N.BF = 30 N, friction on the block is 10 N.CC = 20 N, friction on the block is 10 N.DMinimum value of force F to keep block at rest is 20 N.
A block of weight W is held against a vertical wall by applying a horizontal force of 75N . The surface3 of the wall is rough. Now (conside μ<1)
View SolutionA block of mass 'm' is held stationary against a rough wall by applying a force F as shown. Which one of the following statement is incorrect ?
 View Solution
View SolutionA rectangular block is held against a vertical wall by applying a force of 200N normal to the wall. If the frictional froce just prevents the block from sliding down the wall, what is the mass of the block? (The coefficient of static friction between the block and the wall is 0.49)
View SolutionA block of mass 0.1 kg is held against a wall by applying a horizontal force of 5 N on the block. If the coefficient of friction between the block and the wall is 0.5, then the magnitude of the frictional force acting on the block is
View SolutionA block of mass M is held against a rough vertical wall by pressing it with a finger. If the coefficient of friction between the block and the wall is μ and the acceleration due to gravity is g, what is the minimum force required to be applied by the finger to hold the block against the wall?
View Solution

