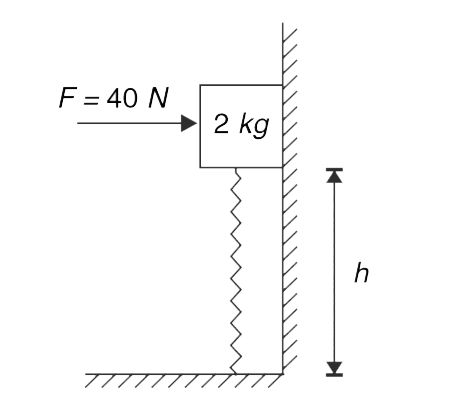
(i) In the arrangement shown in the figure the coefficient of friction between the 2 kg block and the vertical wall is μ=0.5. A constant horizontal force of 40 N keeps the block pressed against the wall. The spring has a natural length of 1.0 m and its force constant is k=400Nm–1. What should be the height h of the block above the horizontal floor for it to be in equilibrium. The spring is not tied to the block.
(ii) A block of mass M is pressed against a rough vertical wall by applying a force F making an angle of θ with horizontal (as shown in figure). Coefficient of friction between the wall and the block is μ=0.75.
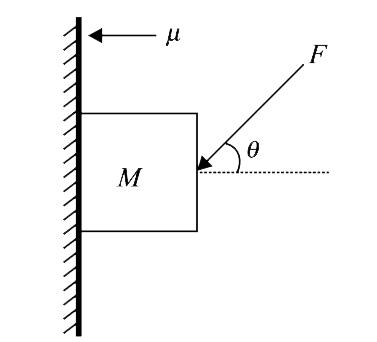
(a) If F = 2 Mg, find the range of values of θ so that the block does not slide
[Take tan37∘=0.75,sin24∘=0.4]
(b) Find the maximum value of θ above which equilibrium is not possible for any magnitude of force F.
The correct Answer is:θ≤13∘
37∘
Topper's Solved these Questions
Similar Questions
A particle is acted upon by a force for 1 second whose X component remains constant at Fx=30N but y and z components vary with time as shown in the graph. Calculate the magnitude of change in momentum of the particle in 1 s. What angle does the change in momentum (Δ→P) make with X axis ?

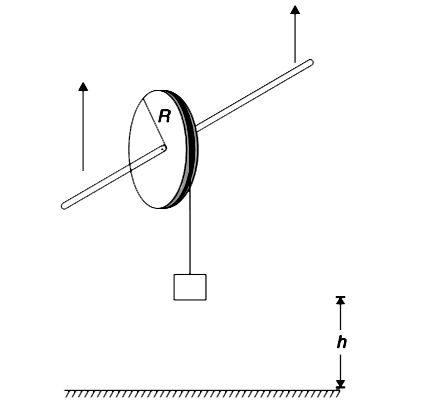
View SolutionThe pulley of radius R can rotate freely about its axle as shown in the figure. A thread is tightly wrapped around the pulley and its free end carries a block of mass m. When the block is at a height h above the ground the system is released (i.e., the pulley is made free to rotate & the block is allowed to fall) and at the same instant the axle is moved up keeping it horizontal all the time. When the block hits the floor the axle has gone up by a distance 2h. Find the angle by which the pulley must have rotated by this time.
View SolutionA block of mass 2 kg is pushed against a rough vertical wall with a force os 40 N. Coefficient of static friction being 05. Another horizontal force is 15 N, is applied on the block in a direction paralle to the wall. Will the block move? If yes in which direction? If no, find the frictional force exerted by the wall on the block.
View SolutionA block of mass m is pressed against a wall by a spring as shown in the figure. The spring has natural length , l (l gt L) , and the coefficient of friction between the block and the wall is mu . The minimum spring constant K necessary for equilibrium is:
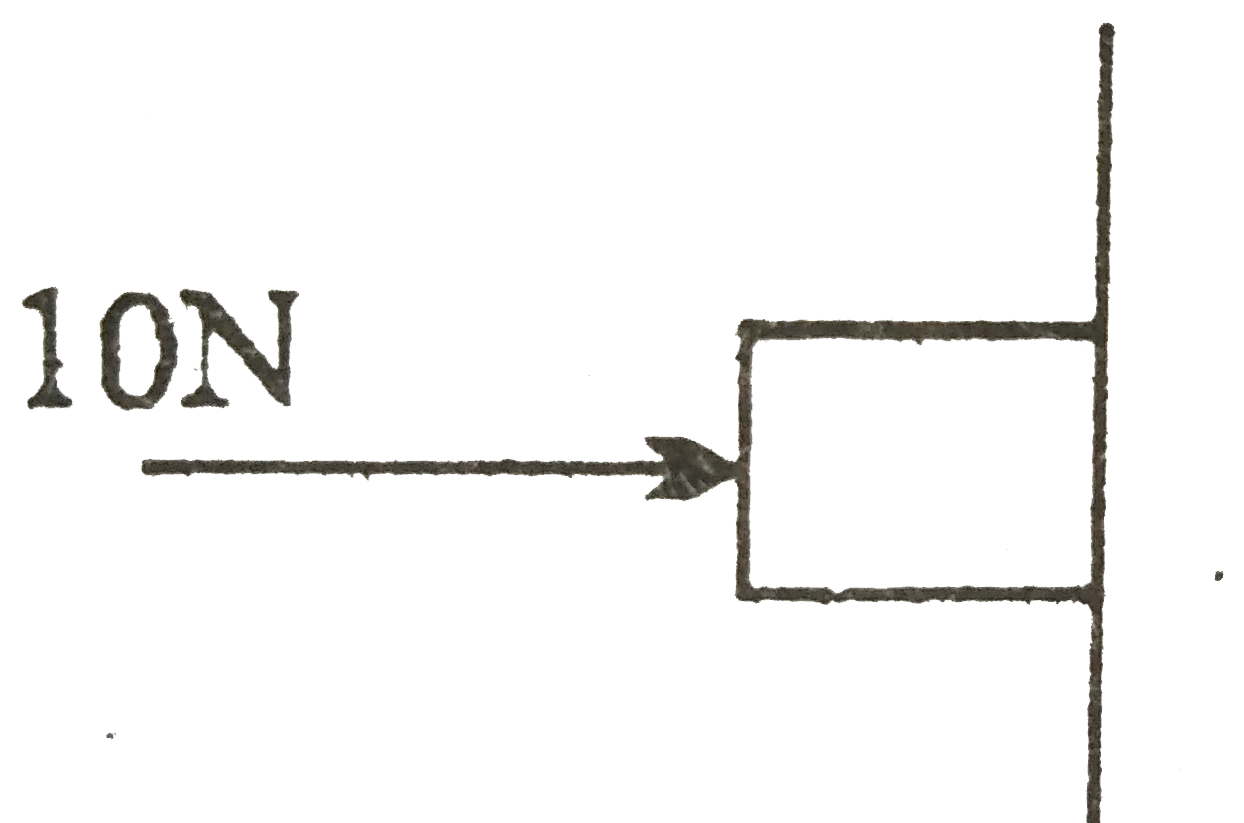
View Solutionकिसी दीवार के विरुद्ध एक गुटके को स्थिर बनाये रखने के लिए 10 न्यूटन के क्षैतिज बल की आवश्यकता होती है | यदि दीवार और गुटके के मध्य घर्षण गुणांक 0.2 हो , तो गुटके का भार होगा -
View SolutionA block of mass 0.1 kg is kept pressed onto a wall by applying a horizontal force of 5 N. If the coefficient of friction between the block and the wall is 0.5, find the force of friction on the block.
View SolutionA block of mass 0.1 kg is kept pressed against a wall by applying a force of 5 N horizontally on the block. Coefficient of friction between the block and the wall is 0.5. Friction acting on the block is.
View SolutionWhile lifting a 10 kg block vertically with a constant velocity, it is kept pressed against a wall by a horizontal force of 49 N. Coefficient of friction between the block and the wall is 0.2. Find the upward force.
View Solutionblock of mass 0-1 kg is held against a wall by applying a horizontal force of 5 N on the block. If the coefficient of friction between the block and the mass is 0.5, the magnitude of the frictional force acting on the block is :
View SolutionA block of mass 1kg is pressed against a wall by applying a horizontal force of 10N on the block. If the coefficient of friction between the block and the wall is 0.5 ,magnitude of the frictional force acting on the block is
View Solutionकिसी M द्रव्यमान के एक गुटके को उंगलियों से दबाते हुए किसी ऊर्ध्वाधर दीवार से सटाकर रखा गया है। यदि गुटके व दीवार के मध्य घर्षण गुणांक μ है तथा गुरुत्वीय त्वरण g है, तो बताइए कि दीवार के विरुद्ध गुटके को उंगलियों से थामे रखने हेतु कितने न्यूनतम बल को आरोपित करने की आवश्यकता होती है?
View SolutionTwo blocks of masses m1 and m2 are connected by a spring having spring constant K. Initially , the spring is at its natural length. The coefficient of friction between the blocks and the surface is μ. What minimum constant force has to be applied in the horizontal direction to the block of mass m1, in order to shift the other block ?
View SolutionA block of mass 1 kg is pressed against a wall by applying a horizontal force of 10N on the block. If the coefficient of friction between the block and the wall is 0.5, magnitude of the frictional force acting on the block is
View SolutionA block of mass 2 kg is pushed against a rough vertical wall with a force is 40 N. Coefficient of static friction being 0.5. Another horizontal force is 15 N, is applied on the block in a direction parallel to the wall. Will the block move? If yes in which direction? If no, find the frictional force exerted by the wall on the block.
View SolutionA block of mass 1 kg is pressed against a wall by applying a horizontal force of 10 N on the block. If the coefficient of friction between the block and the wall is 0.5, magnitude of the frictional force acting on the block is
View Solution
