What is the time required for a block to slide down from the top to the bottom ofan inclined plane 6.4 m long if the inclination of the plane with the horizonta l is 30° and the coefficient of friction= 0.2?
2s
1.5s
3s
2.5s
The correct Answer is:A
The downward component of force mg sinθ is opposed by the frictional force F=μR=μmgcosθ
∴ Resultant downward force=mg(sinθ−μcosθ)
∴ a=Fm=g(sinθ−μcosθ)
But(sinθ−μsinθ)=sin30∘−μcos30∘
=[0.5−210×1.7322]
=0.3268
When the block slides from the top to the bottom of the inclined plane,
s=12at2
∴ 6.4=12g(sinθ−μcosθ)t2
∴ 6.4=12×9.8×0.3268×t2=1.6t2
∴ t2=6.41.6=4
∴ t=2s
Topper's Solved these Questions
- FRICTIONAL IN SOLIDS AND LIQUIDS BOOK - MARVEL PUBLICATIONCHAPTER - FRICTIONAL IN SOLIDS AND LIQUIDS EXERCISE - TEST YOUR GRASP
10 Videos
- FORCE, WORK AND TORQUEBOOK - MARVEL PUBLICATIONCHAPTER - FORCE, WORK AND TORQUEEXERCISE - TEST YOUR GRASP
10 Videos
- MAGNETIC EFFECT OF ELECTRIC CURRENT BOOK - MARVEL PUBLICATIONCHAPTER - MAGNETIC EFFECT OF ELECTRIC CURRENT EXERCISE - TEST YOUR GRASP
10 Videos
Similar Questions
A block slides down on inclined plane (angle of inclination 60∘ ) with an accelration g/2 Find the coefficient friction

View SolutionA block is kept on a inclined plane of inclination q of length l. The velocity of particle at the bottom of inclined is (the coefficient of friction is μ
View Solution
Knowledge Check
A body is on the point of sliding down an inclined plane under its own weight. If the inclination of the plane to the horizon be 30∘, the angle of friction will be
A3∘B60∘C45∘D15∘A block is placed on an inclined plane. The angle of inclination of the plane is such that the block slides down the plane at a constant speed. The coefficient of kinetic friction is
AsinθBcosθCcotθDtanθA block is projected upwards with a velocity of 5 m/s from the bottom of a rough inclined plane of inclination 30° with the horizontal. It stops after 0.5 s. What is the coefficient of friction ? (g=10m/s2)
A√3B1√3C√2D√5
A block is placed on the top of a plane inclined at 37∘ with horizontal. The length of the plane is 5m. The block slides down the plane and reaches the bottom.
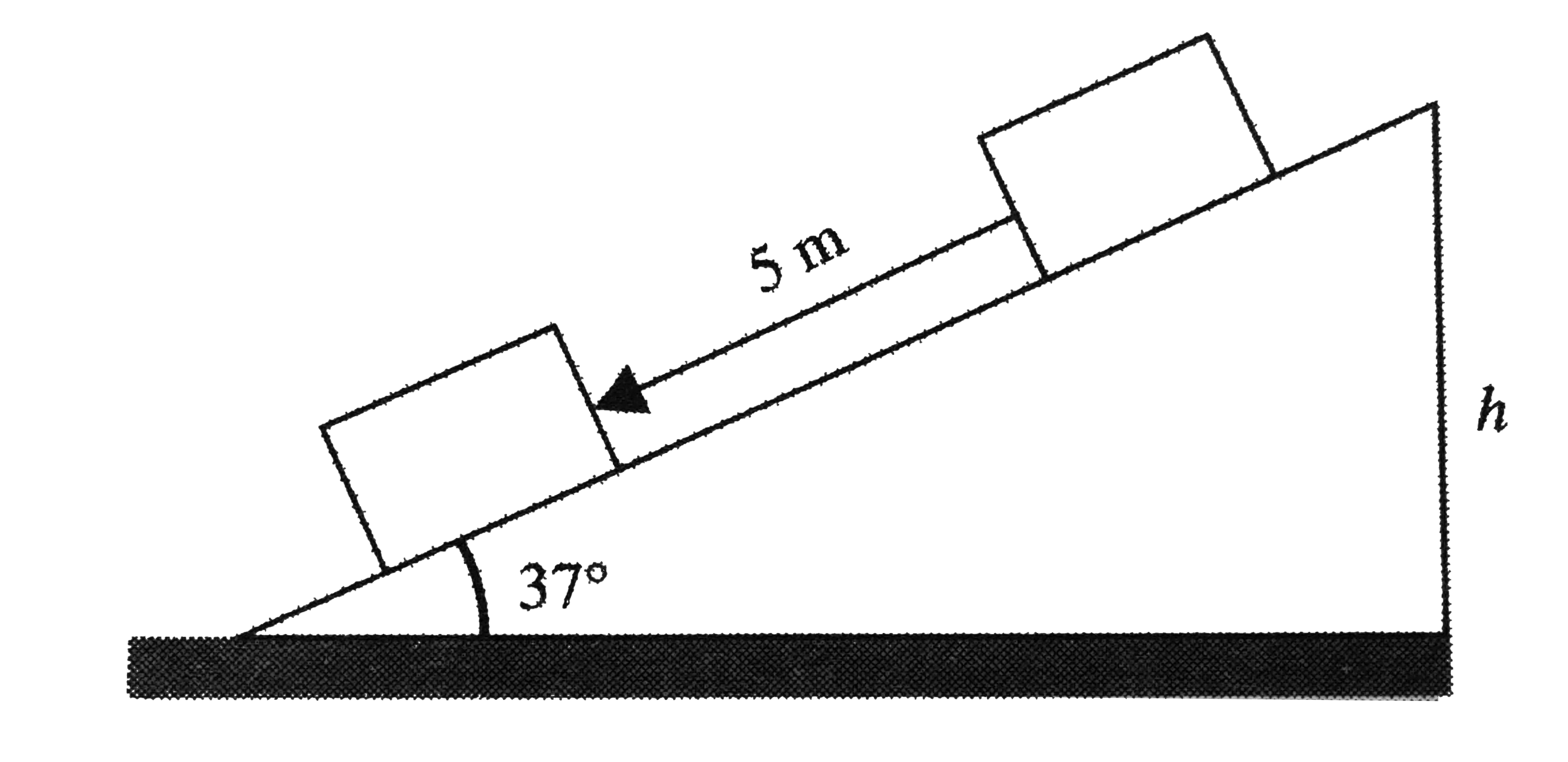
a. Find the speed of the block at the bottom if the inclined plane is smooth.
b. Find the speed of the block at the bottom if the coefficient of friction is 0.25.
View SolutionA block is gently placed at the top of an inclined plane 6.4 m long . Find the time taken by the block to slide down to the bottom of the plane . The plane makes an angle30∘ with the horizontal Coefficient of friction between the block and the plane is 0.2 Take g=10m/s2 .
View SolutionA block of mass m moves with constant speed down the inclined plane of inclination θ. Find the coefficient of kinetic friction.

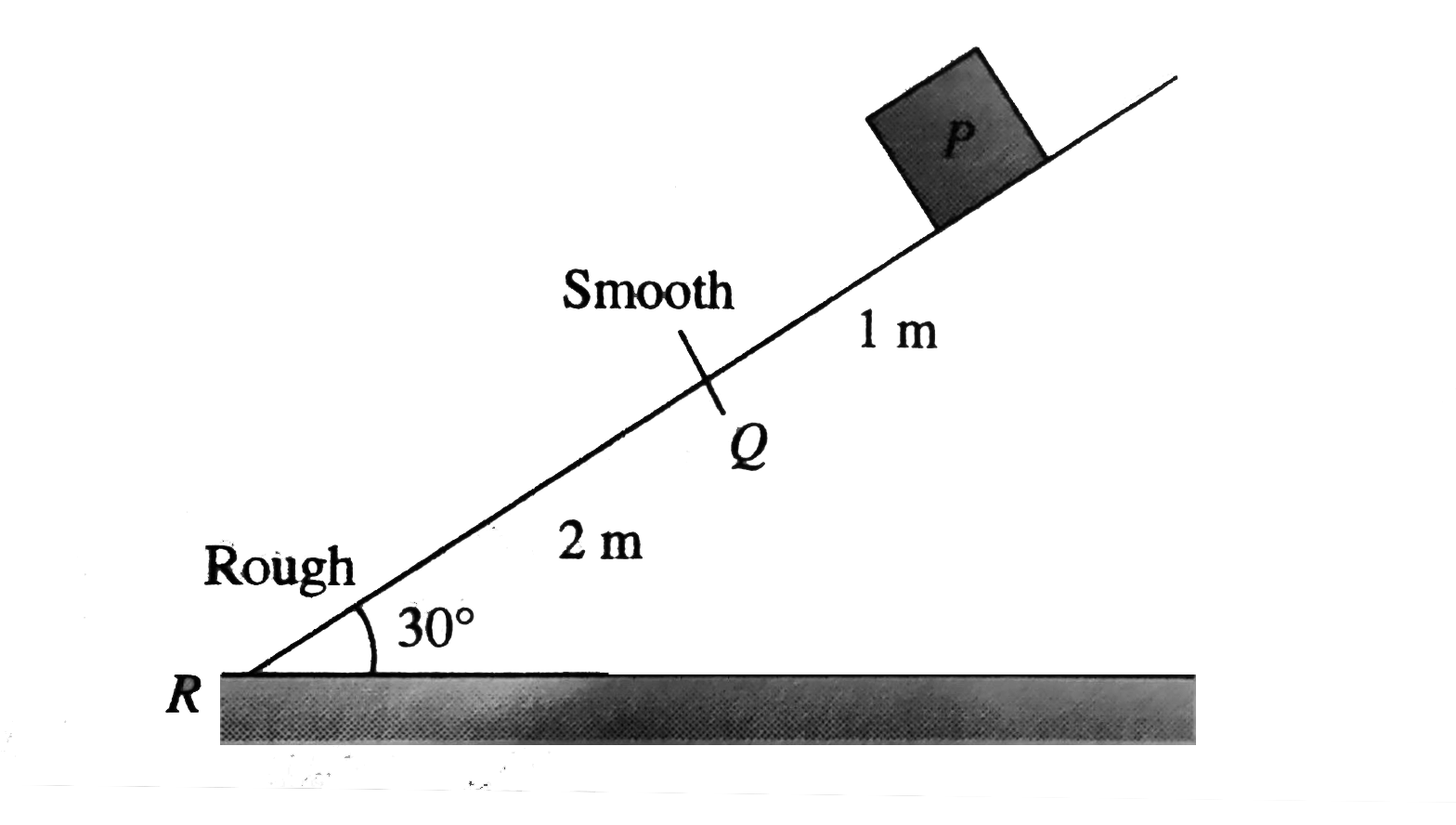
View SolutionA block of mass 5.0kg slides down from the top of an inclined plane of length 3m. The first 1m of the plane is smooth and the next 2m is rough. The block is released from rest and again comes to rest at the bottom of the plane. If the plane is inclined at 30∘ with the horizontal, find the coefficient of friction on the rough portion.
View SolutionA block is kept on an inclined plane of inclination θ of length l. the velocity of particle at the bottom of inclined is (the coefficient of friction is μ)
View Solution
