A block is gently placed at the top of an inclined plane 6.4 m long . Find the time taken by the block to slide down to the bottom of the plane . The plane makes an angle30∘ with the horizontal Coefficient of friction between the block and the plane is 0.2 Take g=10m/s2 .
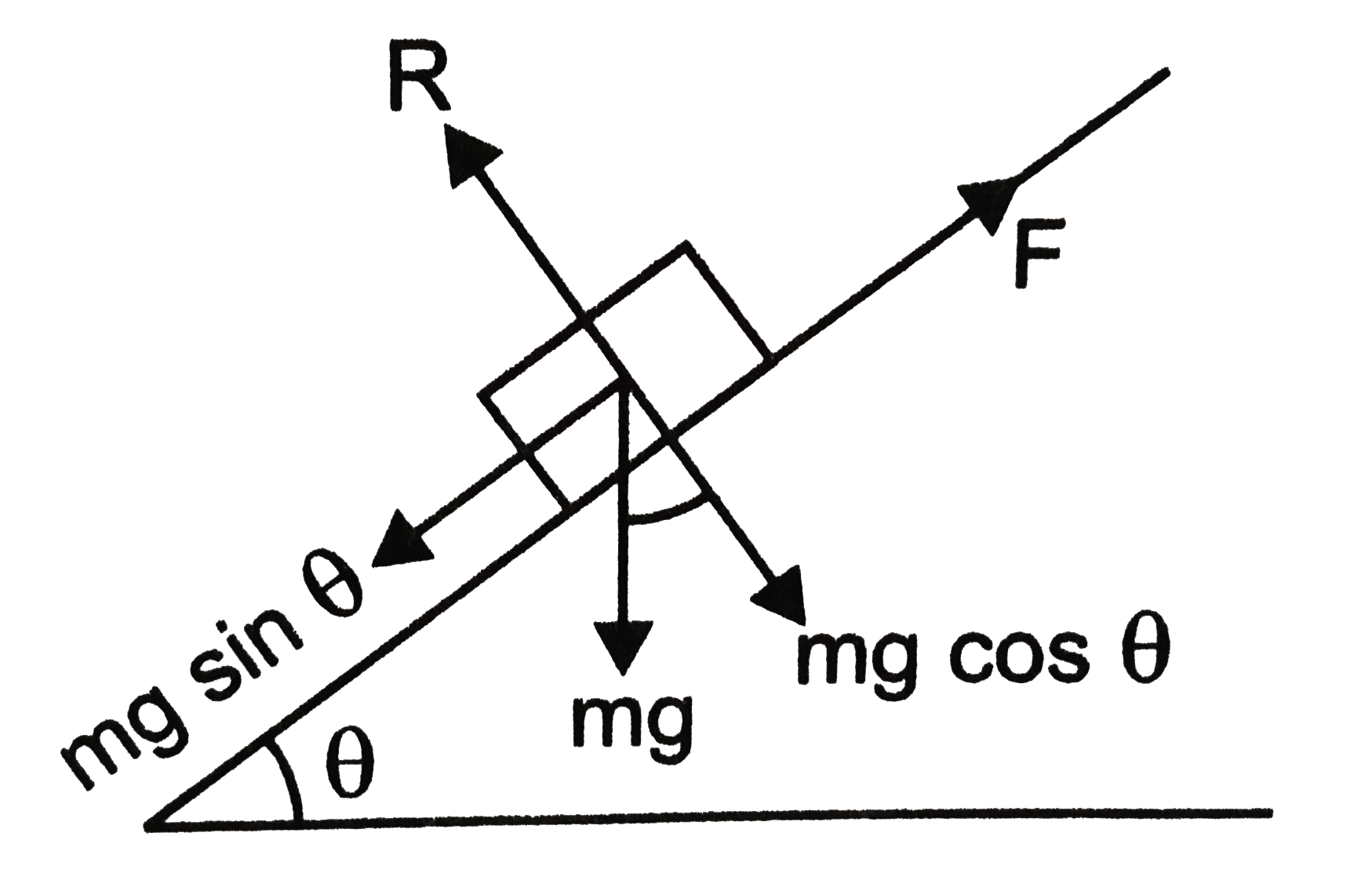
As the block is sliding down the inclined plane force of friction F acts up the plane If a is acceleration produced in the block then net force on the block down the plane is
f=ma=mgsinθ−F=mgsinθ−μR
=mgsinθ−μmgcosθ
=mg(sinθ−μcosθ)
or a=g(sinθ−μcosθ)
=10(sin30∘−0.2cos30∘)
=10(12−0.2√32)
a=5(1−0.2×1.732)=5×0.6536
=3.268m/s2
Now s=6.4m,
u=0 as the block starts from rest
t=?
From s=ut+12at2
6.4=0+12×3.268t2
t=√2×6.43.268=1.98s
 .
.
Topper's Solved these Questions
- LAWS OF MOTIONBOOK - PRADEEPCHAPTER - LAWS OF MOTIONEXERCISE - Very short answer questions
73 Videos
- LAWS OF MOTIONBOOK - PRADEEPCHAPTER - LAWS OF MOTIONEXERCISE - Long Answer Questions
16 Videos
- LAWS OF MOTIONBOOK - PRADEEPCHAPTER - LAWS OF MOTIONEXERCISE - solved examples
104 Videos
- KINEMATICSBOOK - PRADEEPCHAPTER - KINEMATICSEXERCISE - 1 NCERT Comprehension
4 Videos
- MATHEMATICAL TOOLSBOOK - PRADEEPCHAPTER - MATHEMATICAL TOOLSEXERCISE - Fill in the blanks
5 Videos
Similar Questions
Knowledge Check
A block of mass m slides down an inclined plane which makes an angle θ with the horizontal. The coefficient of friction between the block and the plane is μ. The force exerted by the block on the plane is
AmgcosθB√μ2+1mgcosθCμmgcosθ√μ2+1DμmgθA block of mass 2kg rests on a rough inclined plane making an angle of 30∘ with the horizontal. The coefficient of static friction between the block and the plane is 0.7. The frictional force on the block is
A9.8NB0.7×9.8×√3NC9.8×√3ND0.7×9.8NA block is stationary on an inclined plane If the coefficient of friction between the block and the plane is μ then
 .Aμ>tanθBf=mgsinθCf=μmgcosθDthe reaction of the ground on the block is mg cos θ
.Aμ>tanθBf=mgsinθCf=μmgcosθDthe reaction of the ground on the block is mg cos θ
A block of mass 8 kg is sliding on a surface inclined at an angle of 45∘ with the horizontal. Calculate the acceleration of the block. The coefficient of friction between the block and surface is 0.6. (Take g=10m/s2)
View SolutionA block of mass 8 kg is sliding on a surface inclined at an angle of 45∘ with the horizontal . Calculate the acceleration of the block . The coefficient of friction between the block and surface is 0⋅6 ( Take g = 10m/s2)
View SolutionA block of mass 5 kg is placed on a rough inclined plane. The inclination of the plane is gradually increased till the block just begins to slide down. The inclination of the plane is than 3 in 5. The coefficient of friction between the block and the plane is (Take, g=10m/s2)
View SolutionA body takes just twice the time as long to slide down a plane inclined at 30∘ to the horizontal as if the plane were frictionless. The coefficient of friction between the body and the plane is
View SolutionA block of 4kg slides down an inclined plane which makes an angle θ=60∘ with the horizontal. The co-effcient of friction between the block and the plane is μ=3/4. The force exerted by the block on the plane is (g=10m/s2)
View Solution
