A concave lens having a material of refractive index μ1 is kept in a medium of R.I. μ2, where μ1<μ2. A parallel beam of light is incident on the lens. The concave lens will act as
a diverging lens
a converging lens
a plane glass slab
a plano concave lens
The correct Answer is:B
To solve the problem, we need to analyze the behavior of a concave lens when it is placed in a medium with a higher refractive index than that of the lens material. Here’s a step-by-step solution:
Step 1: Understand the Properties of the Concave Lens
A concave lens is a diverging lens that typically causes parallel rays of light to diverge. The lens has a negative focal length, and it is thinner at the center than at the edges.
Step 2: Identify the Refractive Indices
We are given that:
- The refractive index of the lens material is μ1.
- The refractive index of the medium surrounding the lens is μ2.
- It is stated that μ1<μ2, meaning the lens is in a denser medium.
Step 3: Analyze the Incident Light
A parallel beam of light is incident on the concave lens. In typical scenarios, when light travels from a medium of lower refractive index to a medium of higher refractive index, it bends towards the normal.
Step 4: Apply Snell's Law
Using Snell's Law, we can analyze how the light rays behave at the interface of the lens and the surrounding medium. Since μ2>μ1, the light rays will bend towards the normal when entering the lens.
Step 5: Determine the Effect of the Lens
In this scenario, because the light rays are bending towards the normal upon entering the lens, the concave lens will not behave as it typically does in air (or a less dense medium). Instead, the rays will converge rather than diverge.
Conclusion
Thus, in this specific case where the concave lens is placed in a medium of higher refractive index, the concave lens will act as a converging lens.
Final Answer
The concave lens will act as a converging lens when placed in a medium with a higher refractive index.
---
A concave lens is a diverging lens that typically causes parallel rays of light to diverge. The lens has a negative focal length, and it is thinner at the center than at the edges.
We are given that:
- The refractive index of the lens material is μ1.
- The refractive index of the medium surrounding the lens is μ2.
- It is stated that μ1<μ2, meaning the lens is in a denser medium.
A parallel beam of light is incident on the concave lens. In typical scenarios, when light travels from a medium of lower refractive index to a medium of higher refractive index, it bends towards the normal.
Using Snell's Law, we can analyze how the light rays behave at the interface of the lens and the surrounding medium. Since μ2>μ1, the light rays will bend towards the normal when entering the lens.
In this scenario, because the light rays are bending towards the normal upon entering the lens, the concave lens will not behave as it typically does in air (or a less dense medium). Instead, the rays will converge rather than diverge.
Thus, in this specific case where the concave lens is placed in a medium of higher refractive index, the concave lens will act as a converging lens.
The concave lens will act as a converging lens when placed in a medium with a higher refractive index.
Topper's Solved these Questions
- RAY OPTICS (MIRRORS, LENSES AND OPTICAL INSTRUMENTS)BOOK - MARVEL PUBLICATIONCHAPTER - RAY OPTICS (MIRRORS, LENSES AND OPTICAL INSTRUMENTS)EXERCISE - TEST YOUR GRASP
10 Videos
- MEASUREMENTS BOOK - MARVEL PUBLICATIONCHAPTER - MEASUREMENTS EXERCISE - TEST YOUR GRASP
10 Videos
- REFRACTION OF LIGHT BOOK - MARVEL PUBLICATIONCHAPTER - REFRACTION OF LIGHT EXERCISE - Test Your Grasp
10 Videos
Similar Questions
A concave lens made of a material of refractive index n1 is kept in a medium of refractive index n2. A parallel beam of light is incident on the lens. Complete the path of rays of light emerging from the concave lens (i) n1>n2 (ii) n1=n2 (iii) n1<n2.
View SolutionA thin bi-convex lens made out of a material of refractive index μ1 is place in a medium of refractive index μ2. A paraxial beam of light, parallel to the principal axis of the lens, is shown in the figure. Based on the ray diagram, we can conclude that

View Solution
Knowledge Check
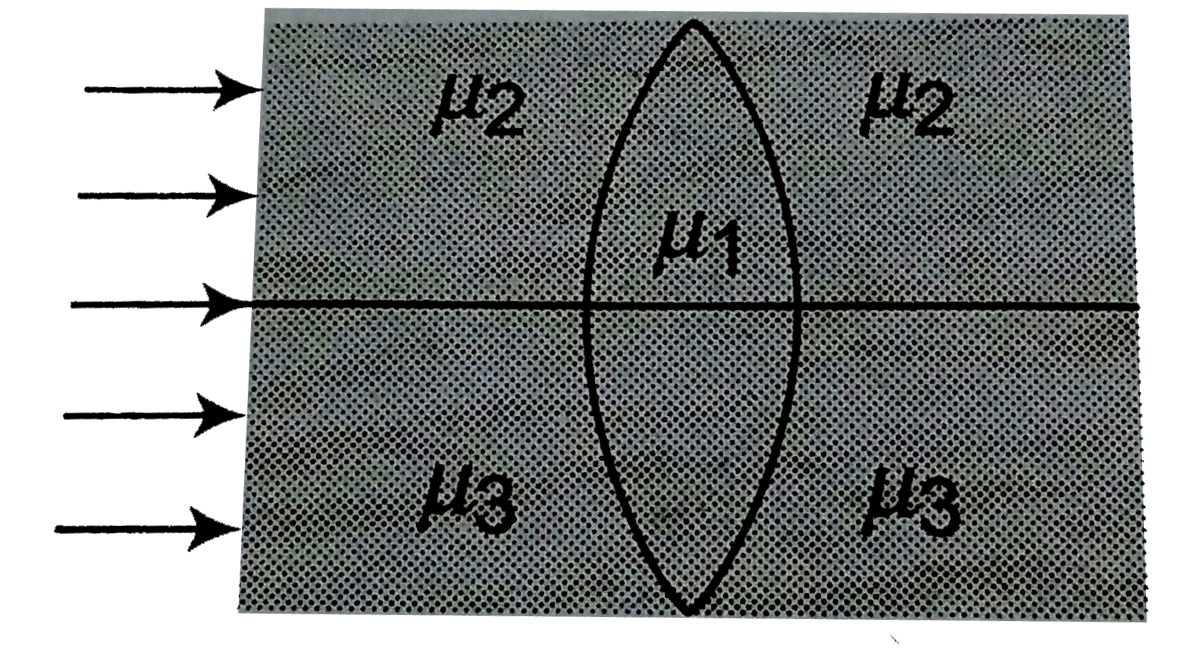
A double convex lens made of a material of refractive index μ1, is placed inside two liquids of refractive indices μ2 and μ3 as shown (μ1>μ2>μ3) A wide parallel beam of light is incident on the lens from the left. The lens will give rise toAa single convergent beamBtwo different convergent beamsCtwo different divergent beamsDa convergent and a divergent beamA double convex lens, lens made of a material of refractive index μ1, is placed inside two liquids or refractive indices μ2 and μ3, as shown. μ2>μ1>μ3. A wide, parallel beam of light is incident on the lens from the left. The lens will give rise to
 Aa single convergent beamBtwo different convergent beamsCtwo different divergent beamsDa convergent and a divergent beam
Aa single convergent beamBtwo different convergent beamsCtwo different divergent beamsDa convergent and a divergent beamA lens made of material of Refractive index μ2 is surrounded by a medium of Refractive Index μ1. The focal length f is related as
Af∝(μ2−μ1)Bf∝μ1(μ2−μ1)Cf∝(μ2+μ1)Df∝1(μ2+μ1)
An equiconvex lens of refractive index μ2 is placed such that the refractive :
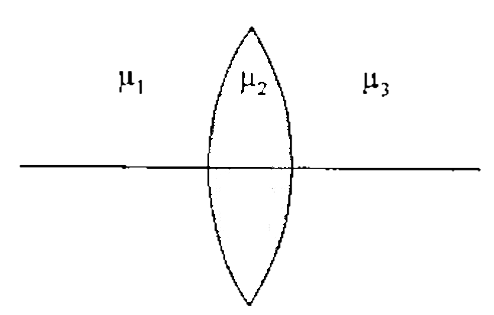
View SolutionThe refractive index of the material of a concave lens is nv It is immersed in a medium of refractive index n2. A parallel beam of light is incident on the lens. Trace the path of emergent rays
View SolutionThe refractive index of the material of a concave lens is n. It is immersed in a medium of refractive index n1. A paprallel beam of light is incident on the lens. Trace the path of emerged rays in each of the following cases :
(a) n1>n (b) n1<n ( c) n1=n.
View SolutionA concave lens made of material of refractive index 1.6 is immersed in a medium of refractive index 2.0 The two surfaces of the concave lens have the same radius of curvature 0.2 m. The lens will behave as a
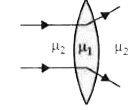
View SolutionA convex lens made up of material of refractive index μ1, is immersed in a medium of refractive index μ2 as shown in the figure. The relation between μ1 and μ2 is
View Solution
