A particle executing a linear SHM has velocities of 8 m/s 7 m/s and 4 m/s, respectively at three points at dis"tan"ces of x m, (x+1) m and (x+2)m from the mean position. What is the maximum velocity of the particle ?
√50ms
√65ms
√35ms
√20ms
The correct Answer is:B
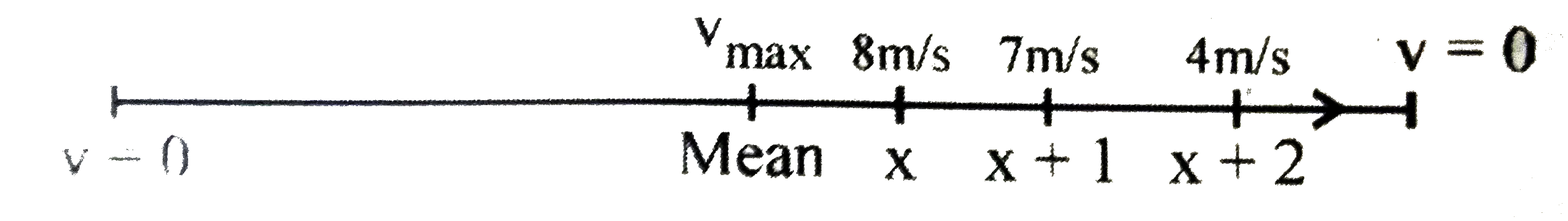
v1=8 atx,v2=7 at x+1andv3=4 at x+2
In S.H.M., v=ω√A2−x2∴v2=ω2(A2−x2)
∴64=ω2(A2−x2)
49=ω2[A2−(x+1)2]
16=ω2[A2−(x+2)2]
∴64−49=ω2[A2−x2−(A2−(x2+2x+1))]
∴15=ω2[−x2+(x2+2x+1)]=ω2(2x+1)
and 64−16=ω2[A2−x2−(A2−(x2+4x+4))]
48=ω2[−x2+x2+4x+4]=ω24x+4)
Dividing (4) by (5), we get
1548=516=2x+14x+4
∴20x+20=32x+16
∴12x=4∴x=13
and from (4), ω2=152x+1=152×13+1=9
∴ω=±3rad/s
and from (1), 64=9(A2−19)=9A2−1
∴9A2=65∴A2=659∴A=√653
and Maximum velocity =ωA
=3×√653=√65m/s
Topper's Solved these Questions
Similar Questions
A particle performing S.H.M. has velocities of 8 cm/s and 6 cm/s at displacements of 3 cm and 4 cm respectively. Calculate the amplitude and period of S.H.M.
View SolutionA particle is executing a linear S.H.M. Its velocity at a distance x from the mean position is given by v2=144−9x2. The maximum velocity of the particle is
View Solution
Knowledge Check
A particle executing linear SHM has velocities v1 and v2 at dis"tan"ce x1 and x2, respectively from the mean position. The angular velocity of the particle is
A ⎷x21−x22v22−v21B ⎷v22−v21x21−x22C ⎷x21+x22v22+v21D ⎷v22+v21x21+x22A particle is executing a linear S.H.M. v1 and v2 are as speeds at dis"tan"ces x1 and x2 from the equilibrium position. What is its ampiltude of oscillation ?
AA= ⎷v21x22−v22x21v21−v22BA= ⎷v21−v22v21x22−v22x21CA=v21x22−v22x21v21−v22DA= ⎷v21x21−v22x22v21−v22A particle executing linear S.H.M. has velocities v1 and v2 at distances x1 and x2 respectively from the mean position. The angular velocity of the particle is
A ⎷x21−x22v22−v21B ⎷v22−v21x21−x22C ⎷x21+x22v22+v2D ⎷v22+v21x22+x21
When a particle executing a linear S.H.M. moves from its extreme position to the mean position, its
View SolutionA particle executes a linear S.H.M. of amplitude 8 cm and period 2s. The magnitude of its maximum velocity is
View Solutionparticle is executing S.H.M. If its amplitude is 2 m and periodic time 2 seconds , then the maximum velocity of the particle will be
View SolutionA particle is executing S.H.M. Ifu1 and u2 are the velocitiesof the particle at distancesx1 andx2 from the mean position respectively, then
View SolutionA particle performing S.H.M. about equilibrium position. Then the velocity of the particle is
View Solution
