Question

In Young's double slit experiment, the two slits are at a distance 'd' apart. Interference pattern is observed on a screen at a distance D front the slit, if at a point on the screen, directly opposite to the slits, the first dark fringe is observed, then wave length of the wave will be

Options

A. `lamda=(d^(2))/(2D)`
B. `lamda=(d^(2))/(D)`
C. `lamda=(2d^(2))/(D)`
D. `lamda=(D)/(d^(2))`

Answer

B

Explanation

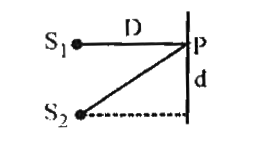
`S_(2)=(D^(2)+d^(2))^(1//2)`
`=D[1+(d^(2))/(D^(2))]^(1//2)=D[1+(d^(2))/(2D^(2))]`
`therefore S_(2)P-S_(1)P=D+(d^(2))/(2D^(2))-D=(d^(2))/(2D)`
For the first dark band, pathh difference`=(lamda)/(2)`
`therefore (d^(2))/(2D)=(lamda)/(2)" "therefore lamda=(d^(2))/(D)`