Two parallel plate air capacitance of same capacity C are connected in series to a battery of emf E. Then one of the capacitors is completely filled with dielectric material of constant K. The change in the effective capacity of the series combination is
C2[K−1K+1]
2C[K−1K+1]
C2[K+1K−1]
C2[K−1K+1]2
The correct Answer is:A
Two parallel plate capacitors are connected in series,
∴ Theire resultant capacity C1=C×CC+C=C2
and when one of then is completely filled with a dielectric, its capacity becomes KC.
∴ new resultant capacity
1C2=1C+1KC=KC+CC⋅(KC)=C(K+1)C(KC)
∴C2=KCK+1
∴ The change in the capacitance
ΔC=C2−C1
=CKK+1=C2
=C[KK+1−12]
=C[2K−K−12(K+1)]
ΔC=C2[K−1K+1]
Topper's Solved these Questions
- BOOK - MARVEL PUBLICATIONCHAPTER - ELECTROSTATICSEXERCISE - TEST YOUR GRASP20videos
ELECTROSTATICS
- BOOK - MARVEL PUBLICATIONCHAPTER - ELECTRONS AND PHOTONS EXERCISE - TEST YOUR GRASP - 1715videos
ELECTRONS AND PHOTONS
- BOOK - MARVEL PUBLICATIONCHAPTER - GRAVITATION EXERCISE - TEST YOUR GRASP -220videos
GRAVITATION
Similar Questions
Two parallel plate capacitors of capacitance C each are connected in series with a battery of emf ε. Then, one of the capacitors is filled with a dielectric of dielectric constane K.
i. Find the change in electric field in the two capacitors, if any
ii. What amount of charge flows through the battery?
iii Find the change in the energy stored in the circuit, if any.View SolutionTwo parallel plate capacitors, each of capacitance 40 muF, are connected is series. The space between the plates of one capacitor is filled with a dielectric material of dielectric constant K =4. Find the equivalent capacitacne of the system.
View Solution
Knowledge Check
- Question 1 - Select One
Two identical parallel plate air capacitors are connected in series to a battery of emf V. If one of the capacitor is completely filled with dielectric material of constant K, then potential difference of the other capacitor will become
AKV(K+1)BKVK+1CK−1KVDVK(K−1) - Question 2 - Select One
Two parallel plate air filled capacitors each of capacitance C, are joined in series to a battery of emf V. The space between the plates of one of the capacitors is then completely filled up with a uniform dielectric having dielectric constant K. The quantity of charge which flows through the battery is -
ACV2(K−1K+1)BCV2(K+1K−1)CCV(K−1K+1)DCV(K+1K−1) - Question 3 - Select One
Two identical parallel plate capacitors of capacitance C each are connected in series with a battery of emf, E as shown. If one of the capacitors is now filled with a dielectric of dielectric constant k, the amount of charge which will flow through the battery is (neglect internal resistance of the battery)
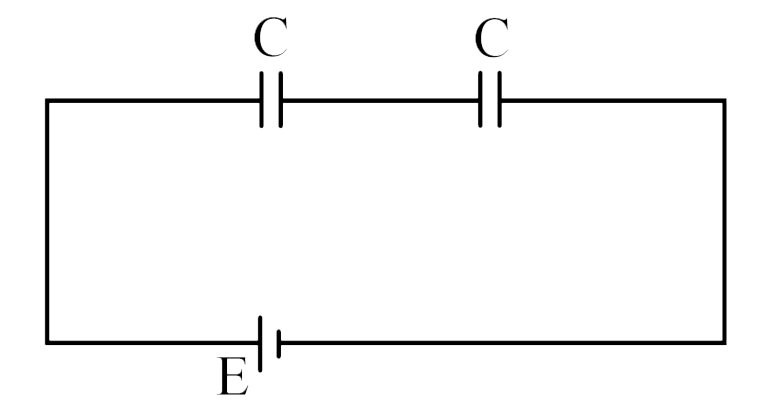Ak+12(k−1)CEBk−12(k+1)CECk−2k+2CEDK+2k−2CE
Two parallel plate air capacitance C, were connected in series to a battery with emf ξ. Then one of the capacitors was filled up with uniform dielectric with permittivity ε. How many times did the electric field strength in that capacitor decrease ? What amount of charge flows throgh the battery ?
View SolutionTwo parallel plate air capacitors, each of capacitance C=50 were connected is series ot emf ε=100V. Then one of the capacitors was filled with a uniforme dielectirc of relative permittivity ε=5 Compare the before and after the insertion of the dielectric? What amout of charge flows from the battery?
View SolutionA parallel plate capacitor of capacitance 10μF is connected across a battery of emf 5 mV. Now, the space between the plates of the capacitors is filled with a deielectric material of dielectric constant K=5. Then, the charge that will flow through the battery till equilibrium is reached is
View SolutionA parallel plate air capacity 'C' farad, potential 'V' volt and energy 'E' joule . When the gap between the plates is completely filled with dielectric
View SolutionTwo identical parallel plate air capacitors are connected in series to a battery of emf V. If one of the capacitor is completely filled with dielectric material of constant K, then potential difference of the other capacitor will become
View Solution