f(x) ,g(x), h(x) all are continuos and differentiable functions in [a,b] also a<c<b and f(a)= g(a)=h(a). Point of intersection of the tangent at x=c with chord joining x=a and x=b is on the left of c in y= f(x) and on the right in y=h(x). And tangent at x=c is parallel to the chord in case of y=g(x). Now answer the following questions.
If f(b)=g(b)=h(b), then
f'(c)=g'(c)=h'(c)
f'(c)>g'(c)>h'(c)
f'(c)<g'(c)<h'(c)
None of these
The correct Answer is:C
Topper's Solved these Questions
- MONOTONICITY MAXIMA AND MINIMABOOK - ARIHANT MATHSCHAPTER - MONOTONICITY MAXIMA AND MINIMAEXERCISE - Exercise (Single Integer Answer Type Questions)
11 Videos
- MONOTONICITY MAXIMA AND MINIMABOOK - ARIHANT MATHSCHAPTER - MONOTONICITY MAXIMA AND MINIMAEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
31 Videos
- MONOTONICITY MAXIMA AND MINIMABOOK - ARIHANT MATHSCHAPTER - MONOTONICITY MAXIMA AND MINIMAEXERCISE - Exercise (Statement I And Ii Type Questions)
9 Videos
- MATRICES BOOK - ARIHANT MATHSCHAPTER - MATRICES EXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
49 Videos
- PAIR OF STRAIGHT LINES BOOK - ARIHANT MATHSCHAPTER - PAIR OF STRAIGHT LINES EXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
2 Videos
Similar Questions
f(x),g(x)andh(x) are all continuous and differentiable functions in [a,b]. Also a<c<b and f(a)=g(a)=h(a). Point of intersection of the tangent at x=c with chord joining x=a and x=b is on the left of c in y=f(x) and on the right in y=h(x). And tangent at x=c is parallel to the chord in case of y=g(x). Now answer the following questions.
If c=a+b2 for each b, then:
View SolutionGraph of y=f(x)andy=g(x) is given in the following figure. If h(x)=f(g(x)), then find the value of h'(2).
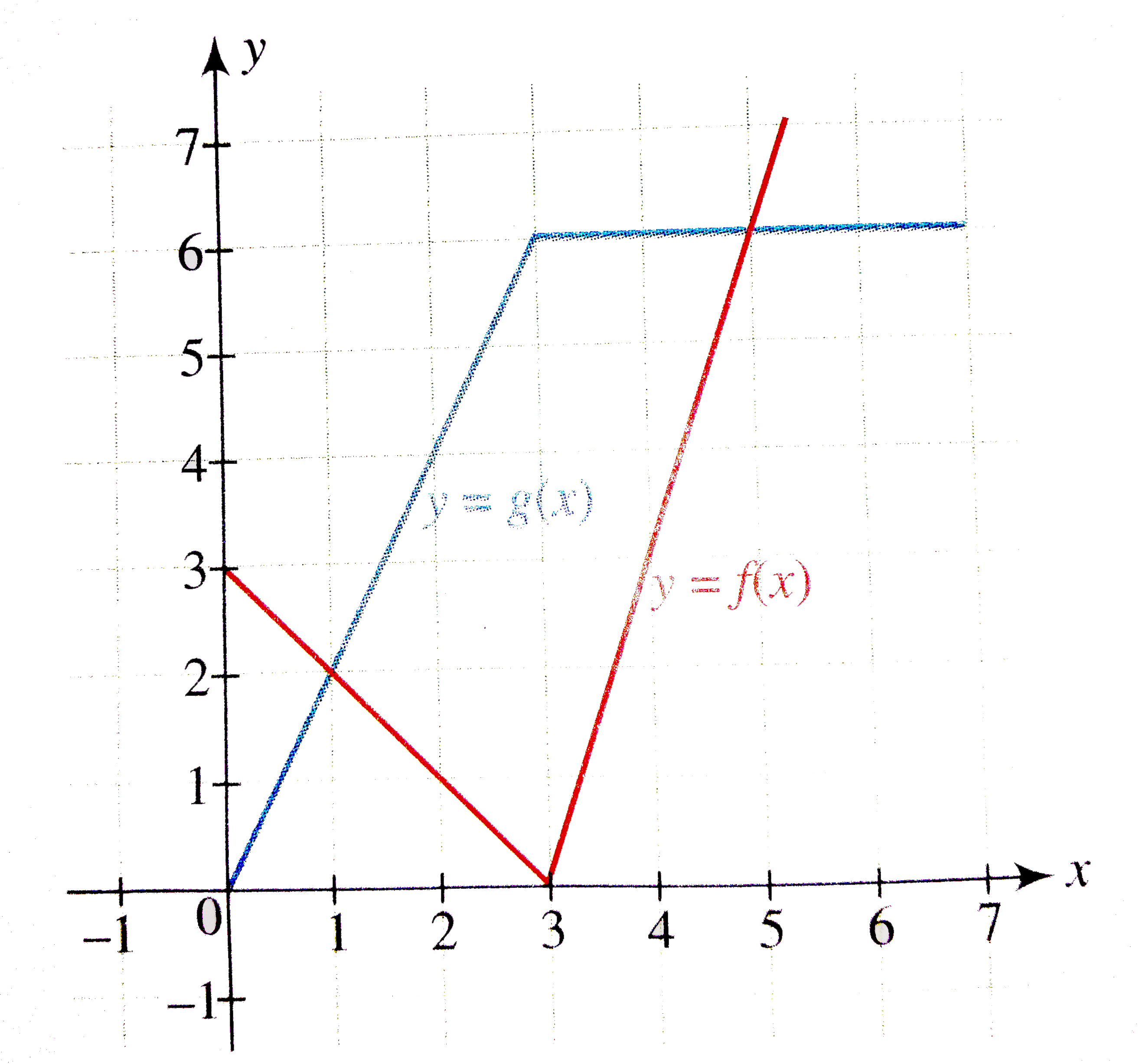
View Solution
Knowledge Check
f(x) ,g(x), h(x) all are continuos and differentiable functions in [a,b] also a<c<b and f(a)= g(a)=h(a). Point of intersection of the tangent at x=c with chord joining x=a and x=b is on the left of c in y= f(x) and on the right in y=h(x). And tangent at x=c is parallel to the chord in case of y=g(x). Now answer the following questions.
If f'(x)>g'(x)>h'(x), thenAf(b)<g(b)<h(b)Bf(b)>g(b)>h(b)Cf(b)≤g(b)≤h(b)Df(b)≥g(b)≥h(b)f(x) ,g(x), h(x) all are continuos and differentiable functions in [a,b] also a<c<b and f(a)= g(a)=h(a). Point of intersection of the tangent at x=c with chord joining x=a and x=b is on the left of c in y= f(x) and on the right in y=h(x). And tangent at x=c is parallel to the chord in case of y=g(x). Now answer the following questions.
If c=a+b2 for each b, thenAg(x)=Ax2+Bx+cBg(x)=logxCg(x)=sinxDg(x)=exf and g differentiable functions of x such that f(g(x))=x, If g'(a)≠0 and g(a)=b, then f'(b)=
Ag(a)B1g(a)C−g'(a)D1g'(a)
Graph of y=f(x)andy=g(x) is given in the following figure. If h(x)=f(g(x)), then find the value of h'(2).

View SolutionIf f(x) is a twice differentiable function such that f''(x)=−f(x),f'(x)=g(x),h(x)=f2(x)+g2(x)andh(10)=10 , then h (5) is equal to
View SolutionLet f be a twice differentiable function such that fx=−f(x),andf′(x)=g(x),h(x)=[f(x)]2+[g(x)]2. Find h(10)ifh(5)=11
View SolutionIf f(x) is a twice differentiable function such that f''(x)=−f,f'(x)=g(x),h(x)=f2(x)+g2(x)andh(10)=10 , then h (5) is equal to
View SolutionIf the function f(x):A→B and g(x):B→C are defined such that (g(f(x)))−1 exist then f(x)andg(x) are
View Solution
