Graph of $y = f (x) and y = g (x)$ is given in the following figure. If $h (x) = f (g (x))$ , then find the value of $h' (2)$ .

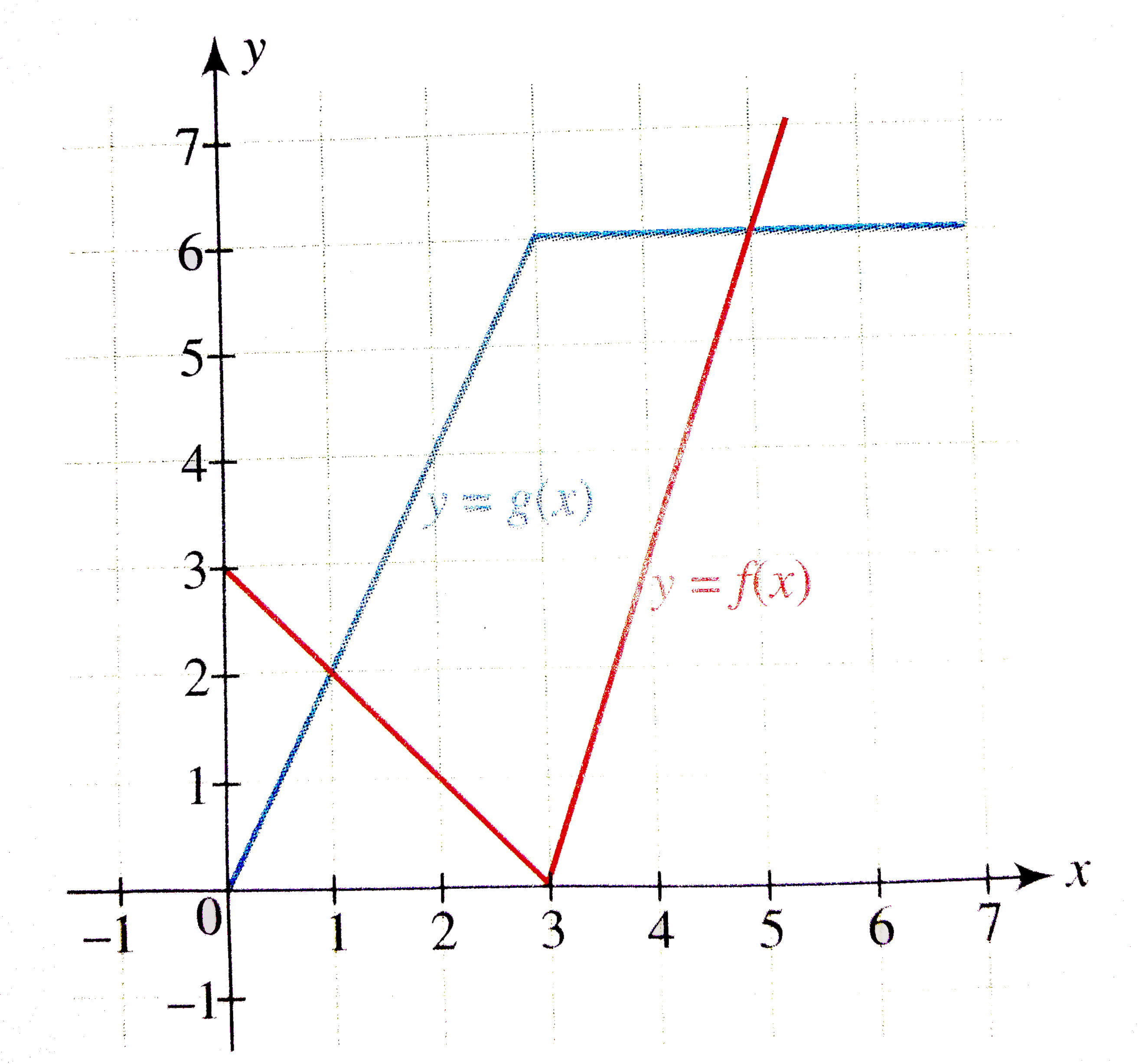
Text Solution

Verified by Experts

$h' (2) = f' (g (2)) g' (2)$
$g' (2)$ is the slope of the line passing through the points $(0, 0) and (3, 6)$
$∴ g' (2) = 2$
Also $g (2) = 4$
$∴ h' (2) = f' (4) \times 2$
Now $f' (4)$ is the slope of the line passing through the pointps $(3, 0) and (5, 6)$
$∴ f' (4) = 3$
$∴ h' (2) = 3 \times 2 = 6$

|

Updated on:21/07/2023

Class 12 MATHS FUNDAMENTAL OF MATHEMATICS

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
A horse covers a distance of 1500 meters in 1 minute 20 seconds. At what speed the horse is running?
A67.9 km/hr
B67. 5 km/hr
C67.7 km/hr
D67.2 km/hr
Question 2 - Select One
$[m]$ is defined as the greatest integer less than m
$[m]$ is defined as the least integer greater than m.
$f (x, y) = {x} + [y]$
$g (x . Y) = [x] - {y}$
$F (f (x, y)) = {f (x, y)} = [g (x, y)]$
$G (g (x, y)) = [f (x, y)] - {g (x, y)}$
Given that $x^{2} = 4 and y^{2} = 9 and | F (f (x, y)) | = | G (g (x, y)) |$ then find the value of $x + y$ :
A $- 1$
B0
C1
D5
Question 3 - Select One
Given $f (x) = \frac{1}{(1 - x)} . g (x) = f (f (x)) and h (x) = f (f (f (x)))$ , then the value of $f (x) . g (x) . h (x)$ is :
A0
B $- 1$
C1
D2

CENGAGE-GRAPHS OF ELEMENTARY FUNCTIONS -Exercise

Home
Ask Doubt
Profile