Given , the edges A, B and C of triangle ABC. Find cos∠BAM, where M is mid-point of BC.
The correct Answer is:sinC+sinB⋅sinA√sin2C+sin2B+2sinB⋅sinC⋅sinA
Step by step video, text & image solution for Given , the edges A, B and C of triangle ABC. Find cosangleBAM, where M is mid-point of BC. by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
- BOOK - ARIHANT MATHSCHAPTER - PRODUCT OF VECTORSEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)52videos
PRODUCT OF VECTORS
- BOOK - ARIHANT MATHSCHAPTER - PRODUCT OF VECTORSEXERCISE - Exercise (Single Integer Answer Type Questions)16videos
PRODUCT OF VECTORS
- BOOK - ARIHANT MATHSCHAPTER - PROBABILITYEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)55videos
PROBABILITY
- BOOK - ARIHANT MATHSCHAPTER - PROPERTIES AND SOLUTION OF TRIANGLES EXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)21videos
PROPERTIES AND SOLUTION OF TRIANGLES
Similar Questions
Prove that the resultant of the vectors represented by the sides −−→AB and −−→AC of a triangle ABC is 2−−→AD, where D is the mid - point of [BC].
View SolutionP and Q are respectively the mid-points of sides AB and BC of a triangle ABC and R is the mid-point of AP, show that
ar(ΔPRQ) = 1/2 ar(ΔARC)View Solution
Knowledge Check
- Question 1 - Select One
The triangle is formed by joining the mid-points of the sides AB,BC and CA of △ABCand the area of △PQR is 6cm2, then the area of △ABC is :
A36cm2B12cm2C18cm2D24cm2 - Question 2 - Select One
In ABC, G is the centroid, AB = 15 cm, BC = 18 cm and AC = 25 cm. Find GD, where D is the mid-point of BC.
A13√86 cmB23√86 cmC83√15Dnone of these - Question 3 - Select One
In ABC, G is the centroid, AB = 15 cm, BC = 18 cm and AC = 25 cm. Find GD, where D is the mid-point of BC.
A13√86cmB23√86cmC83√15cmDnone of these
In the given figure, find angle ∠AEB. If Angle ∠B is the right angle of triangle ABC and D is the mid point of side BC.
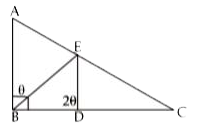 View Solution
View SolutionIn ΔABC,G is the centroid , AB=15cm, BC=18 cm, and AC=25 cm . Find GD , Where D is the mid point of BC:
View SolutionIn the given figure ABC is a right angled triangle with ∠B=90∘ . D is the mid -point of BC . Show that AC2=AD2+3CD2 .
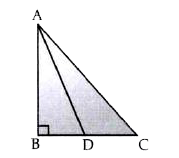 View Solution
View SolutionD is the mid-point of side AB of the triangle ABC.E is the mid-point of CD and F is the mid-point of AE. Prove that 8× area of (ΔAFD)= area of ΔABC
View SolutionBM and CN are perpendiculars to a line passing through the vertex A of a triangle ABC. If Lis the mid-point of BC, prove that LM = LN.
View Solution

