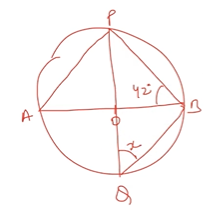
Given vectors where O is the centre of circle circumscribed about , then find vector
The correct Answer is:
Step by step video, text & image solution for Given vectors barCB=bara, barCA=barb and barCO=barx where O is the centre of circle circumscribed about DeltaABC, then find vector barx by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
- BOOK - ARIHANT MATHSCHAPTER - PRODUCT OF VECTORSEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)52videos
PRODUCT OF VECTORS
- BOOK - ARIHANT MATHSCHAPTER - PRODUCT OF VECTORSEXERCISE - Exercise (Single Integer Answer Type Questions)16videos
PRODUCT OF VECTORS
- BOOK - ARIHANT MATHSCHAPTER - PROBABILITYEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)55videos
PROBABILITY
- BOOK - ARIHANT MATHSCHAPTER - PROPERTIES AND SOLUTION OF TRIANGLES EXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)21videos
PROPERTIES AND SOLUTION OF TRIANGLES
Similar Questions
Knowledge Check
- Question 1 - Select One
If the vectors ¯a,¯b and ¯c from the sides BC, CA and AB, respectively, of ΔABC, then
A¯a.¯b+¯b.¯c+¯c.¯a=0B¯aׯb=¯bׯc=¯cׯaC¯a.¯b=¯b.¯c=¯c.¯aD(¯aׯb)+(¯bׯc)+(¯cׯa)=¯0 - Question 2 - Select One
In the given figure, O is the centre of circle, ∠AOB=100∘. Find ∠BCD :
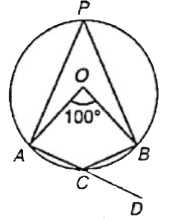 A80∘B60∘C50∘D40∘
A80∘B60∘C50∘D40∘ - Question 3 - Select One
In the given figure, O is the centre of the circle. ∠AOB=70∘, find ∠OCD :
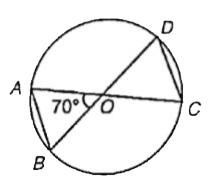 A70∘B55∘C65∘D110∘
A70∘B55∘C65∘D110∘
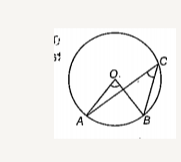
In the given figure, O is the centre of the circle and ∠ACB=25∘ Find ∠AOB
 View Solution
View SolutionIn the figure given below O is the centre of the circle, if θ=60∘, then find angle α
 View Solution
View SolutionIf the volume of parallelepiped determined by vectors (2¯aׯb),(¯bׯ¯¯¯3c) and 5(¯cׯa) is equal to the volume of the parallelepiped determined by vectors 5(¯a+¯b),6(¯b+¯c) and 2(¯c+¯a), then find the volume of parallelepiped determined by vectors ¯,¯b and ¯c in cubic units.
View SolutionIn a given figure, if AB = a, AC = 4 cm, where O is centre of circle and a point D is on BC such that AD ⊥ BC then find length of OD?
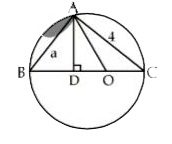 View Solution
View SolutionIf OA=30 cm, then find the radius OB (in cm), where o is the centre of circle.
 View Solution
View Solution