The molecular velocity of any gas is
inversely proportional to absolute temperature
directly proportional to square of temperature
directly proportional to square rooot of temperature
directly proportional to square root of temperature
The correct Answer is:C
(c) The difference type of molecular velocities possessed by gas molecules are
(i) Most probable velocity (α)=√2RTM
(ii) Average velocity ¯v=√8RTπM
(iii) Root mean squre velocity in all three cases
v=√3RTM
In all the above cases
Velocity ∝√T
Topper's Solved these Questions
Similar Questions
Knowledge Check
The average molecular velocity in a gas sample at 300K is 500m/s. The temperature of this gas is increased until the average velocity of its molecules is 1000m/s. what is the new temperature?
A420KB573kC600kD1200kVolume occupied by 1 g molecular weight of any gas is called_
Agram molecular volumeBgram atomic volumeCgram molecule weightDgram atomic weightThe distribution of the molecular velocities of gas molecules at any temperature T is shown below. (The plot below is known as Maxwell's distribution of molecular speeds.)

where
v is molecular velocity
n is number of molecules having velocity v
Let us define ΔNv, which is equal to the number of molecules between the velocity range v and v+Δv, given by
ΔNv=4πNa3e−bv2v2Δv
where
N is total number of molecules
a=√M02πRT and b=M02RT
R is universal gas constant
T is temperature of the gas
M0 is molecular weight of the gas
Answer the following question:
If PPc=Pr, TTc=Tr, and VmVm,c=Vr whereAPr ia reduced pressure, Pc is critical pressureBTr ia reduced temperature, Tc is critical temperatureCVr is reduced volume, Vc is critical volumeDthen the temperature of state (or van der Waals equation), only in terms of Pr, Tr, and Vr is
At the root mean square (rms) speed of a gas X (molecular weight is equal to the most probable speed of gas Y at The molecular weight of the gas Y is :
View SolutionThe distribution of the molecular velocities of gas molecules at any temperature T is shown below. (The plot below is known as Maxwell's distribution of molecular speeds.)
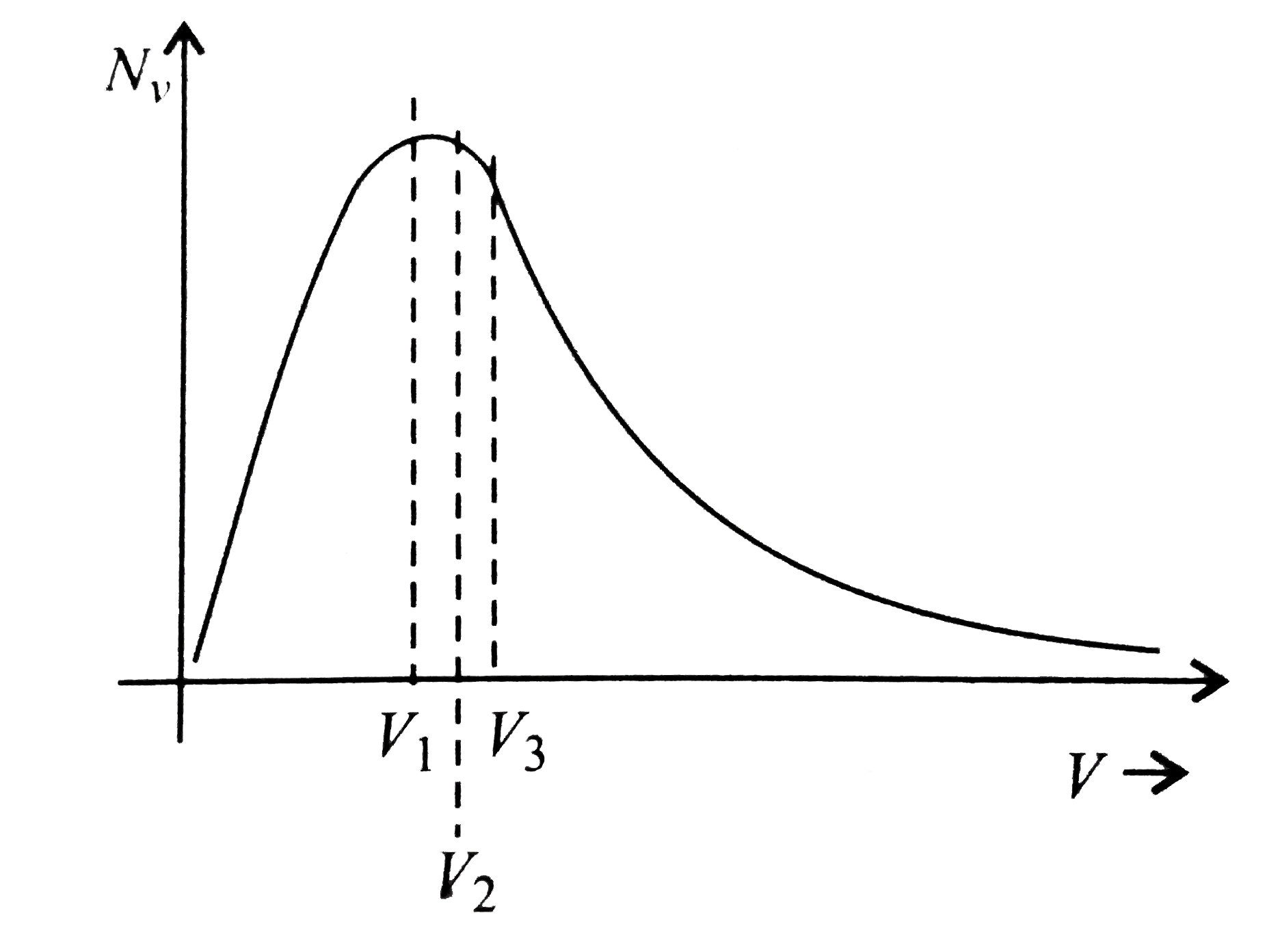
where
v is molecular velocity
n is number of molecules having velocity v
Let us define ΔNv, which is equal to the number of molecules between the velocity range v and v+Δv, given by
ΔNv=4πNa3e−bv2v2Δv
where
N is total number of molecules
a=√M02πRT and b=M02RT
R is universal gas constant
T is temperature of the gas
M0 is molecular weight of the gas
Answer the following question:
SI units of a are
View SolutionThe distribution of the molecular velocities of gas molecules at any temperature T is shown below. (The plot below is known as Maxwell's distribution of molecular speeds.)
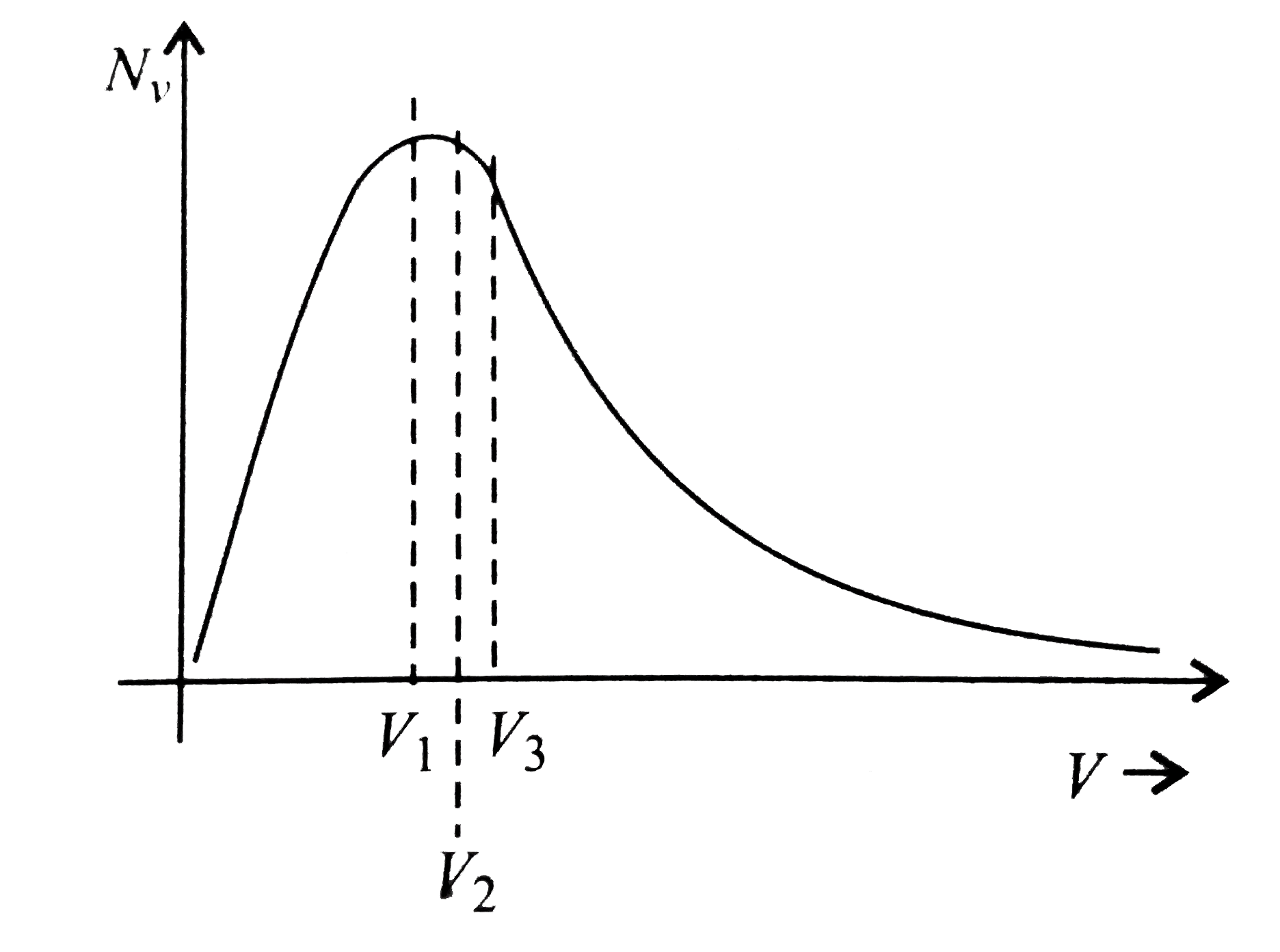
where
v is molecular velocity
n is number of molecules having velocity v
Let us define ΔNv, which is equal to the number of molecules between the velocity range v and v+Δv, given by
ΔNv=4πNa3e−bv2v2Δv
where
N is total number of molecules
a=√M02πRT and b=M02RT
R is universal gas constant
T is temperature of the gas
M0 is molecular weight of the gas
Answer the following question:
SI units of b are
View SolutionThe distribution of the molecular velocities of gas molecules at any temperature T is shown below. (The plot below is known as Maxwell's distribution of molecular speeds.)

where
v is molecular velocity
n is number of molecules having velocity v
Let us define ΔNv, which is equal to the number of molecules between the velocity range v and v+Δv, given by
ΔNv=4πNa3e−bv2v2Δv
where
N is total number of molecules
a=√M02πRT and b=M02RT
R is universal gas constant
T is temperature of the gas
M0 is molecular weight of the gas
Answer the following question:
SI units of b are
View SolutionThe distribution of the molecular velocities of gas molecules at any temperature T is shown below. (The plot below is known as Maxwell's distribution of molecular speeds.)

where
v is molecular velocity
n is number of molecules having velocity v
Let us define ΔNv, which is equal to the number of molecules between the velocity range v and v+Δv, given by
ΔNv=4πNa3e−bv2v2Δv
where
N is total number of molecules
a=√M02πRT and b=M02RT
R is universal gas constant
T is temperature of the gas
M0 is molecular weight of the gas
Answer the following question:
SI units of a are
View Solution
