Molecular velocities
Step by step video solution for Molecular velocities by Chemistry experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Similar Questions
Knowledge Check
The average molecular velocity in a gas sample at 300K is 500m/s. The temperature of this gas is increased until the average velocity of its molecules is 1000m/s. what is the new temperature?
A420KB573kC600kD1200kThe molecular velocity of any gas is
Ainversely proportional to absolute temperatureBdirectly proportional to square of temperatureCdirectly proportional to square rooot of temperatureDdirectly proportional to square root of temperatureThe molecular velocity of any gas is :
Ainversely proportional to absolute temperture.Bdirectly proportional to square of temperatureCdirectly proportional to square root of temperature.Dinversely proportional to the square root of temperature.
Kinetic Theory of Gases | Molecular Velocity and Kinetic Energy
View SolutionMolecular Velocity and Kinetic Energy | REal Gas Analyisis | Liquification of Gases Questions
View SolutionThe viscosity η of a gas is determined by its density ρ, molecular velocity c and its mean free path λ.Show that η=kρcλ where k is a dimensionless constant.
View SolutionThe distribution of the molecular velocities of gas molecules at any temperature T is shown below. (The plot below is known as Maxwell's distribution of molecular speeds.)

where
v is molecular velocity
n is number of molecules having velocity v
Let us define ΔNv, which is equal to the number of molecules between the velocity range v and v+Δv, given by
ΔNv=4πNa3e−bv2v2Δv
where
N is total number of molecules
a=√M02πRT and b=M02RT
R is universal gas constant
T is temperature of the gas
M0 is molecular weight of the gas
Answer the following question:
If PPc=Pr, TTc=Tr, and VmVm,c=Vr where
View SolutionThe distribution of the molecular velocities of gas molecules at any temperature T is shown below. (The plot below is known as Maxwell's distribution of molecular speeds.)
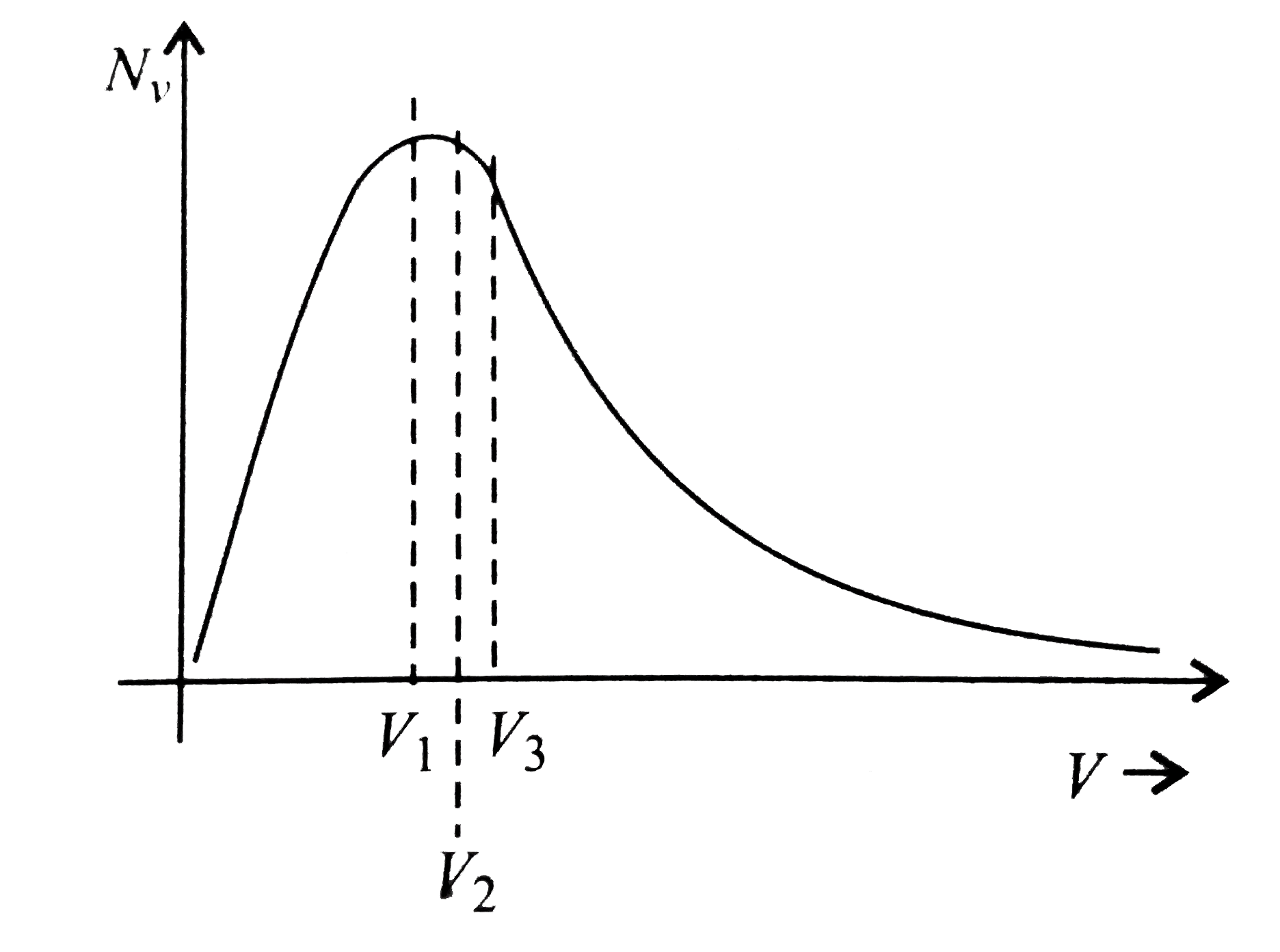
where
v is molecular velocity
n is number of molecules having velocity v
Let us define ΔNv, which is equal to the number of molecules between the velocity range v and v+Δv, given by
ΔNv=4πNa3e−bv2v2Δv
where
N is total number of molecules
a=√M02πRT and b=M02RT
R is universal gas constant
T is temperature of the gas
M0 is molecular weight of the gas
Answer the following question:
SI units of b are
View Solution
