The given arrangement is released from rest when spring is in natural length. Maximum extension in spring during the motion is x0.a1,a2 and a3 are accelerations of the blocks. Make the correct options
_PHY_E01_005_Q01.png)
a2−a1=a1−a3
x0=4mg3k
Velocity of 2m connected to spring when elongation is x02 is v=x02√3k14m
acceleration a1 at x04 is 3kx042m
_PHY_E01_005_S01.png)
2a1=a2+a3
a1−a3=a2−a1
for other options use m equivalent
_PHY_E01_005_S02.png)
Tg'=2(2m)(m)2m+m=4m3
2Tg'=8m3
meq.=4m(2m)m+2m=8m3
_PHY_E01_005_S03.png)
12kx20=8mg3x0
x0=16mg3k
Vx02=Vmax=x02w=x02
⎷k2m+8m3=x02√3k14m
ax04=x04w2=x043k14m=3kx042m
Topper's Solved these Questions
- BOOK - JEE ADVANCED PREVIOUS YEARCHAPTER - JEE ADVANCEDEXERCISE - MULTIPLE CHOICE QUESTIONS22videos
JEE ADVANCED
- BOOK - JEE ADVANCED PREVIOUS YEARCHAPTER - JEE ADVANCEDEXERCISE - SECTION-III (Comprehension Type )3videos
JEE ADVANCED
- BOOK - JEE ADVANCED PREVIOUS YEARCHAPTER - JEE (ADVANCE) 2020EXERCISE - SECTION 36videos
JEE (ADVANCE) 2020
- BOOK - JEE ADVANCED PREVIOUS YEARCHAPTER - JEE ADVANCED 2020EXERCISE - SECTION-36videos
JEE ADVANCED 2020
Similar Questions
The block is allwed to fall, slowly from the position wher spring is in its natural length. Find, maximum extension in the string.
 View Solution
View SolutionBlocks A and B shown in the figure are having equal masses m. The system is released from rest with the spring unstretched. The string between A and ground is cut, when there is maximum extension in the spring. The acceleration of centre of mass of the two blocks at this instant is
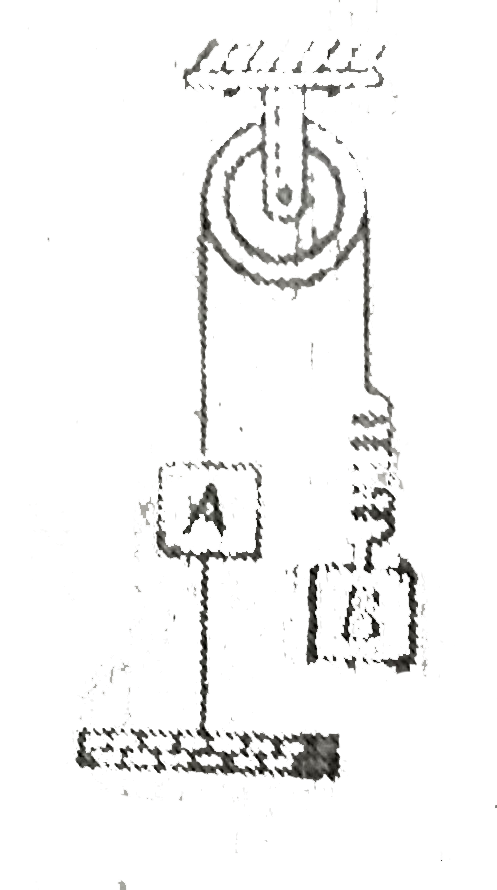 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
In given system a1anda2 are the accelerations of blocks 1 and 2. Then constraint relation is
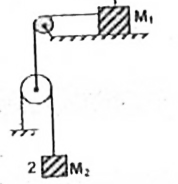 A2a1=a2B2a2=a1Ca1=a2Da1=4a2
A2a1=a2B2a2=a1Ca1=a2Da1=4a2 - Question 2 - Select One or More
Block m is released from rest when spring is in its natural length ( assume pulley is ideal and block does not strike on ground during it's motion in vertical plane )
than :
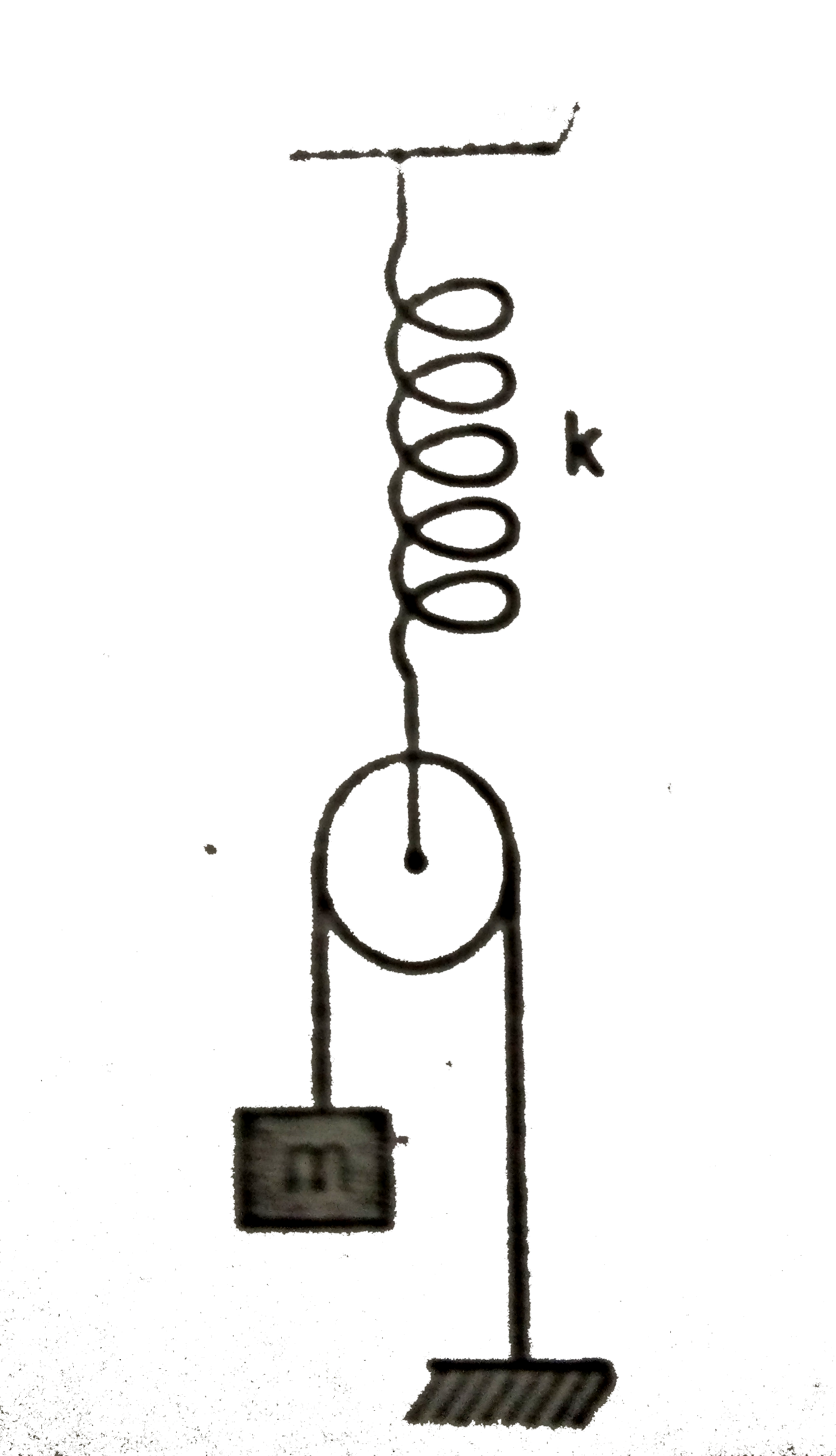 Amaximum elongation in spring is 4mg/kBmaximum elongation in spring is 2mg/kCmaximum speed of block is 2g√mkDmaximum speed of block is g√mk
Amaximum elongation in spring is 4mg/kBmaximum elongation in spring is 2mg/kCmaximum speed of block is 2g√mkDmaximum speed of block is g√mk - Question 3 - Select One
A block of mass 2M is attached to a massless spring with spring-constant k. This block is connected to two other blocks of masses M and 2M using two massless pulleys and strings. The accelerations of the blocks are a1a2 and a3 as shown in the figure. The system is released from rest with the spring in its unstretched state. The maximum extension of the spring is x0 Which of the following option(s) is(are) correct? [g is the acceleration due to gravity. Neglect friction]
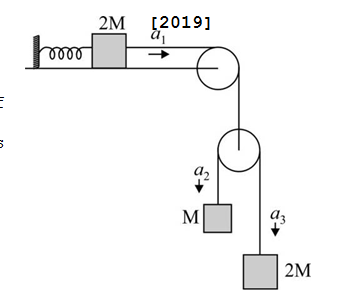 Aa2−a1=a1−a2BAt an extension of x04of the spring, the magnitude of acceleration of the block connected to the spring is 3g10Cx0=4MgkDWhen spring achieves an extension of x02 for the first time, the speed of the block connected to the spring is 3g(M)5K
Aa2−a1=a1−a2BAt an extension of x04of the spring, the magnitude of acceleration of the block connected to the spring is 3g10Cx0=4MgkDWhen spring achieves an extension of x02 for the first time, the speed of the block connected to the spring is 3g(M)5K
Find the relation between acceleration of blocks a1,a2 and a3.
 View Solution
View SolutionConsider the situation shown in figure.
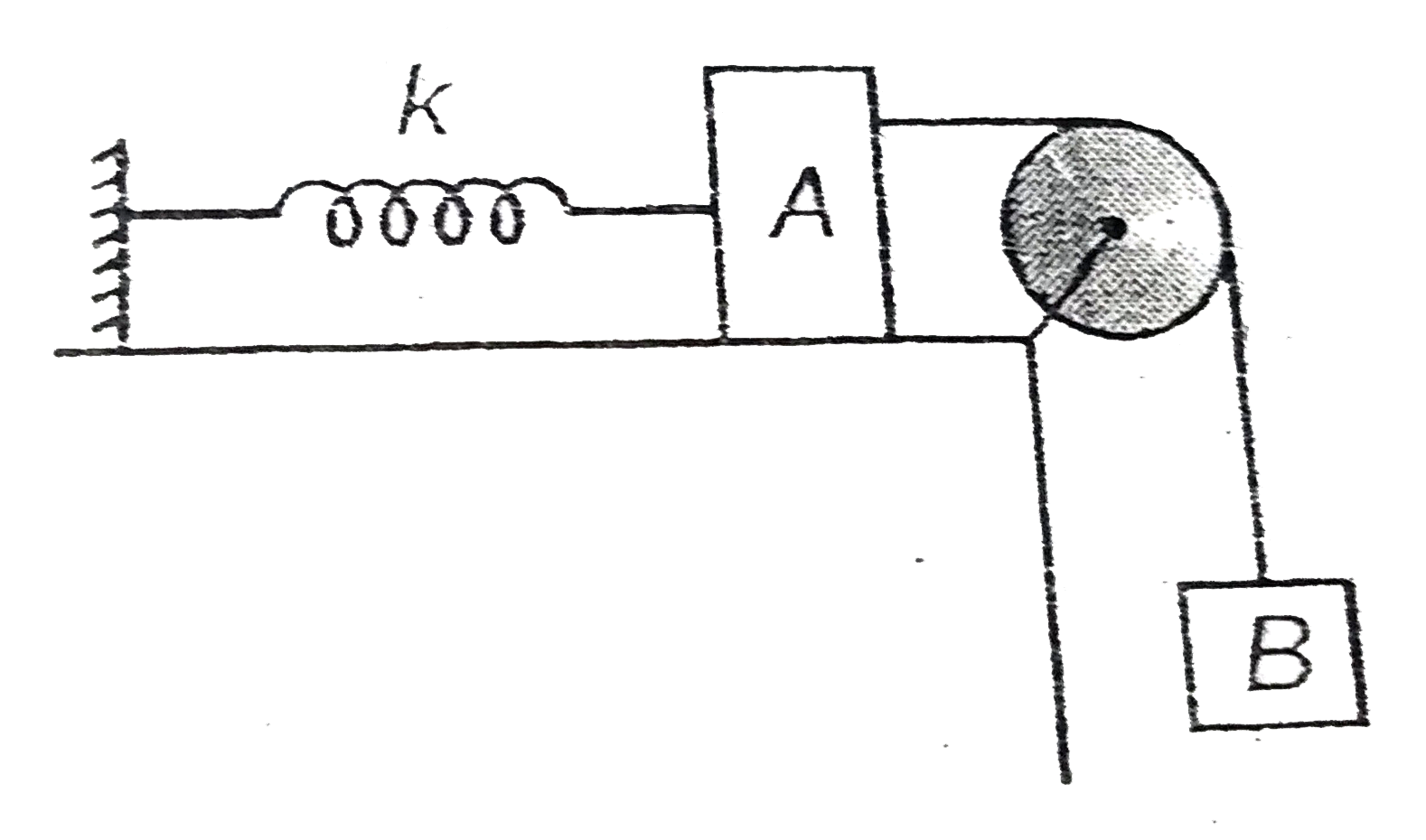
Mass of block A is m and that of blcok B is 2m. The force constant of string is k. Friction is absent everywhere. System is released from rest with the spring unstretched. Find
(a) The maximum extension of the spring xm
(b) The speed of block A when the extension in the springt is x=xm2
(c ) The net acceleration of block B when extension in the spring is x=xm4.View SolutionA block A of mass 2 kg is connected with two springs, as shown . The spring constant of lower spring is system is thrice the spring costant of upper spring. The system is released from rest with both the springs unstreched. The maximum displacement of bloack is 0.1m. Find the acceleration of the block is its lowest position-
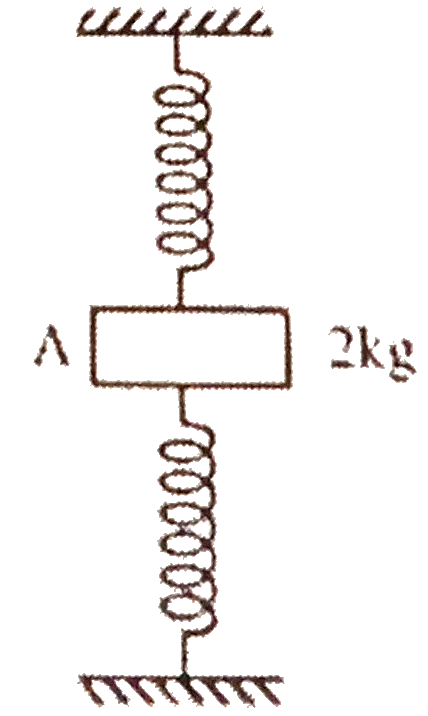 View Solution
View SolutionConsider the arrangement shown. The system is released from rest and the string connecting two blocks is burnt, simultaneously. Maximum extension in the spring (initially releaxed) during the subsequent motion is
 View Solution
View SolutionPassage VII There is a spring block system in a lift moving upwards with acceleration a=g2

If maximum extension in the spring is 5mg2k, then maximum upward accleration (a1) and maximum downward acceleration (a2 of the block areView Solution

