The block is allwed to fall, slowly from the position wher spring is in its natural length. Find, maximum extension in the string.
Since the block falls slowly from rest maximum extension occurs when
mg=Kx0
x0=mgK is maximum extension, Ans.mgK
Topper's Solved these Questions
- SIMPLE HARMONIC MOTION BOOK - RESONANCECHAPTER - SIMPLE HARMONIC MOTION EXERCISE - Board Level Exercise
24 Videos
- SIMPLE HARMONIC MOTION BOOK - RESONANCECHAPTER - SIMPLE HARMONIC MOTION EXERCISE - Exercise- 1, PART - I
25 Videos
- SIMPLE HARMONIC MOTION BOOK - RESONANCECHAPTER - SIMPLE HARMONIC MOTION EXERCISE - Advanced Level Problems
13 Videos
- SEMICONDUCTORSBOOK - RESONANCECHAPTER - SEMICONDUCTORSEXERCISE - Exercise 3
88 Videos
- TEST PAPERSBOOK - RESONANCECHAPTER - TEST PAPERSEXERCISE - FST-3
30 Videos
Similar Questions
Two blocks A and B of masses m & 2m placed on smooth horizontal surface are connected with a light spring. The two blocks are given velocities as shown when spring is at natural length.
(i) Find velocity of centre of mass (b) maximum extension in the spring
View SolutionA block of mass m attached with a an ideal spring of force constant k is placed on a rough inclined plane having inclination θ with the horizontal and coefficient of friction μ=1/2tanθ, Initially the block is held stationary with the spring in its relaxed state, find the maximum extension in the spring if the block is released.
View Solution
Knowledge Check
A block of mass m is placed on a smooth block of mass M=m with the help of a spring as shown in the figure. A velocity v0 is given to upper block when spring is in natural length. Find maximum compression in the spring.
A√m2KV0B√mKv0C√2mKv0D2√mKv0The given arrangement is released from rest when spring is in natural length. Maximum extension in spring during the motion is x0.a1,a2 and a3 are accelerations of the blocks. Make the correct options
_PHY_E01_005_Q01.png)
Aa2−a1=a1−a3Bx0=4mg3kCVelocity of 2m connected to spring when elongation is x02 is v=x02√3k14mDacceleration a1 at x04 is 3kx042mThe system of the wedge and the block connected by a massless spring as shown in the figure is released with the spring in its natural length. Friction is absent. Maximum elongation in the spring will be
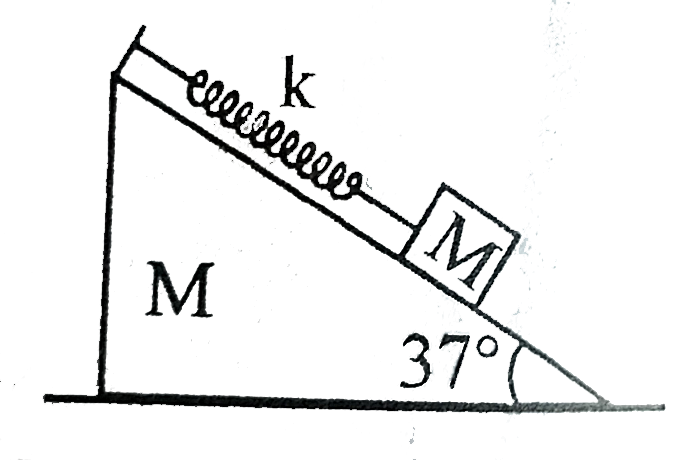A3Mg5kB6Mg5kC4Mg5kD8Mg5k
The block of mass m is released when the spring was in its natrual length. Spring constant is k. Find the maximum elongation of the spring.
View SolutionAn ideal spring with spring constant k is hung from the ceiling and a block of mass M is attached to its lower end. The mass is released with the spring initially unstretched. Then the maximum extension in the spring is
View SolutionA block ofmass m is attached with a spring in its natural length, of spring constant k. The other end A of spring is moved with a constant acceleration 'a' away from the block as shown in the figure−3.74. Find the maximum extension in the spring. Assume that initially block and spring is at rest w.r.t ground frame:
View SolutionA system of wedge and block as shown in figure, is released with the spring in its natural length. All surfaces are frictionless. Maximum elongation in the spring will be
.
View SolutionAn ideal spring having force constant k is suspended from the rigid support and a block of mass M is attached to its lowe end. The mass is released from the natural length of the spring. Then the maximum exiension in the spring is
View Solution