In a hydraulic lift, F1andF2 are the force acting on the small piston and large piston having radii r1andr2 rspectively, then
F1=r22r21F2
F2=r22r21F1
F1=r1r2F2
F1=r2r1F2
The correct Answer is:B
To solve the problem regarding the relationship between the forces F1 and F2 acting on the small and large pistons of a hydraulic lift, we can follow these steps:
1. Understanding the Concept:
In a hydraulic lift, the pressure exerted on both pistons is the same. This is due to Pascal's principle which states that pressure applied to a confined fluid is transmitted undiminished in all directions.
2. Define the Variables:
- Let F1 be the force acting on the small piston.
- Let F2 be the force acting on the large piston.
- Let r1 be the radius of the small piston.
- Let r2 be the radius of the large piston.
3. Calculate the Areas:
The area A of a circle is given by the formula:
A=πr2
Therefore, the areas of the small and large pistons can be expressed as:
- Area of small piston, A1=πr21
- Area of large piston, A2=πr22
4. Set Up the Pressure Equation:
Since the pressure is the same on both sides, we can write:
P1=P2
where P1 and P2 are the pressures on the small and large pistons, respectively. Pressure is defined as force per unit area:
P1=F1A1andP2=F2A2
5. Equate the Pressures:
Substituting the areas into the pressure equation gives:
F1πr21=F2πr22
6. Simplify the Equation:
The π cancels out from both sides:
F1r21=F2r22
7. Rearranging for F1 and F2:
Rearranging the equation to express F1 in terms of F2:
F1=F2⋅r21r22
Alternatively, expressing F2 in terms of F1:
F2=F1⋅r22r21
8. Conclusion:
The relationship between the forces F1 and F2 can be summarized as:
F2=F1⋅r22r21
Final Answer:
Thus, the correct option that represents the relationship between F1 and F2 is:
F2=F1⋅r22r21
In a hydraulic lift, the pressure exerted on both pistons is the same. This is due to Pascal's principle which states that pressure applied to a confined fluid is transmitted undiminished in all directions.
- Let F1 be the force acting on the small piston.
- Let F2 be the force acting on the large piston.
- Let r1 be the radius of the small piston.
- Let r2 be the radius of the large piston.
The area A of a circle is given by the formula:
A=πr2
Therefore, the areas of the small and large pistons can be expressed as:
- Area of small piston, A1=πr21
- Area of large piston, A2=πr22
Since the pressure is the same on both sides, we can write:
P1=P2
where P1 and P2 are the pressures on the small and large pistons, respectively. Pressure is defined as force per unit area:
P1=F1A1andP2=F2A2
Substituting the areas into the pressure equation gives:
F1πr21=F2πr22
The π cancels out from both sides:
F1r21=F2r22
Rearranging the equation to express F1 in terms of F2:
F1=F2⋅r21r22
Alternatively, expressing F2 in terms of F1:
F2=F1⋅r22r21
The relationship between the forces F1 and F2 can be summarized as:
F2=F1⋅r22r21
Thus, the correct option that represents the relationship between F1 and F2 is:
F2=F1⋅r22r21
Topper's Solved these Questions
- FRICTION IS SOLIDS AND LIQUIDS BOOK - TARGET PUBLICATIONCHAPTER - FRICTION IS SOLIDS AND LIQUIDS EXERCISE - MCQ (CRITICAL THINKING)
68 Videos
- FRICTION IS SOLIDS AND LIQUIDS BOOK - TARGET PUBLICATIONCHAPTER - FRICTION IS SOLIDS AND LIQUIDS EXERCISE - MCQ (COMPETITIVE THINKING)
97 Videos
- FORCE BOOK - TARGET PUBLICATIONCHAPTER - FORCE EXERCISE - Evaluation Test
16 Videos
- MAGNETIC EFFECT OF ELECTRIC CURRENT BOOK - TARGET PUBLICATIONCHAPTER - MAGNETIC EFFECT OF ELECTRIC CURRENT EXERCISE - Evaluation Test
12 Videos
Similar Questions
An object of weight 500kgwt is lifted by using a hydraulic press. The radii of the cross sections of the pump piston and press piston are 10 cm and 20 cm, respectively. Calculate the effort required to lift the object. Calculate the displacement of the load if the effort is moved through a distance of 20 cm.
View SolutionAn object of weight 500kgwt is lifted by using a hydraulic press. The radii of the cross sections of the pump piston and press piston are 10 cm and 20 cm, respectively. Calculate the effort required to lift the object. Calculate the displacement of the load if the effort is moved through a distance of 20 cm.
View Solution
Knowledge Check
A biconvex lens made of material with refractive index n2. The radii of curvatures of its left surface and right surface are R1 and R2. The media on its left and right have refreactive indices n1 and n3 respectively. The first and second focal lengths of the lens are respectively f1 and f2.
Assume that R1=R2,n1≠n3. The ratio, f1/f2, of the two focal lengths is equal toA1Bn1/n3Cn3/n1D(n3−1)/(n1−1)A biconvex lens made of material with refractive index n2. The radii of curvatures of its left surface and right surface are R1 and R2. The media on its left and right have refreactive indices n1 and n3 respectively. The first and second focal lengths of the lens are respectively f1 and f2.
The ratio, f1/f2, of the two focal lengths is equal toAn1/n3B(n1−1)/(n3−1)C(n1+1)/(n3+1)D(n2−n3)/(n2−n1)In a hydraulic lift, used at a service station the radius of the large and small piston are in the ration of 20:1. What weight placed on the small piston will be sufficient to lift a car of mass 1500kg ?
A3.75 kgB37.5 kgC7.5 kgD75 kg
In a hydraulic press used for lifting heavy loads, the diameters of smaller and larger pistons are 2 cm and 5 cm, respectively. If the smaller piston is pushed in through 5 cm, then by how much distance will the larger piston move out?
View SolutionIn a hydraulic press, the area of smaller and larger pistons are 5cm2and20cm2, respectively. Calculate the weight which can be raised by larger piston if a force of 100 kgf is applied on smaller piston.
View SolutionIn an arrangement similar to a hydraulic lift, the diameters of smaller and larger pistons are 1.0 cm and 3.0 cm respectively. What is the force exerted on the larger piston when a force of 10 N is applied to the smaller piston?
View SolutionIn a hydraulic press, radii of connecting pipes, r1 and r2 are in the ratio 1:2 . In order to lift a heavy mass M on the larger piston, the small piston must be pressed through a minimum force f equal to
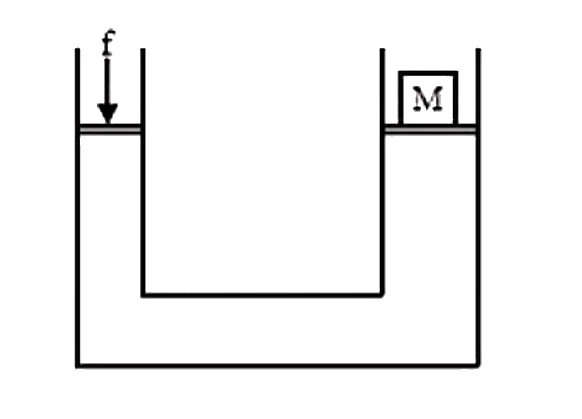
View SolutionIn a hydraulic lift at a service station, the radii of the large and small piston are in the ratio of 20 : 1. What weight placed on the small piston will be sufficient to lift a car of mass 1200 kg ?
View Solution
