A particle is performing linear S.H.M. If the acceleration and corresponding velocity of the particle are ∝ and v respectively and if we plot v2 on Y axis and ∝2 on X axis, then the graph will be
a parabola
a straight line
an ellipse
a hyperbola
The correct Answer is:B
To solve the problem, we need to establish the relationship between the velocity v and acceleration α of a particle performing simple harmonic motion (SHM).
1. Understanding SHM:
- The displacement of a particle in SHM can be expressed as:
x(t)=Asin(ωt+ϕ)
where A is the amplitude, ω is the angular frequency, and ϕ is the phase constant.
2. Finding Velocity:
- The velocity v is the first derivative of displacement with respect to time:
v=dxdt=Aωcos(ωt+ϕ)
3. Finding Acceleration:
- The acceleration α is the derivative of velocity with respect to time:
α=dvdt=−Aω2sin(ωt+ϕ)
4. Relating v and α:
- From the expressions for v and α, we can express v and α in terms of sin(ωt+ϕ) and cos(ωt+ϕ):
v=Aωcos(ωt+ϕ)
α=−Aω2sin(ωt+ϕ)
5. Squaring Both Expressions:
- To relate v2 and α2, we square both equations:
v2=(Aωcos(ωt+ϕ))2=A2ω2cos2(ωt+ϕ)
α2=(−Aω2sin(ωt+ϕ))2=A2ω4sin2(ωt+ϕ)
6. Using the Pythagorean Identity:
- We know that cos2(θ)+sin2(θ)=1. Thus, we can express the relationship:
v2A2ω2+α2A2ω4=1
7. Rearranging the Equation:
- Rearranging gives:
v2A2ω2+α2A2ω4=1
- Let x=α2 and y=v2:
yA2ω2+xA2ω4=1
8. Interpreting the Equation:
- This is a linear equation in the form of yb+xa=1, which represents a straight line in the v2 vs α2 graph.
Conclusion:
- The graph of v2 (on the Y-axis) versus α2 (on the X-axis) will be a straight line.
- The displacement of a particle in SHM can be expressed as:
x(t)=Asin(ωt+ϕ)
where A is the amplitude, ω is the angular frequency, and ϕ is the phase constant.
- The velocity v is the first derivative of displacement with respect to time:
v=dxdt=Aωcos(ωt+ϕ)
- The acceleration α is the derivative of velocity with respect to time:
α=dvdt=−Aω2sin(ωt+ϕ)
- From the expressions for v and α, we can express v and α in terms of sin(ωt+ϕ) and cos(ωt+ϕ):
v=Aωcos(ωt+ϕ)
α=−Aω2sin(ωt+ϕ)
- To relate v2 and α2, we square both equations:
v2=(Aωcos(ωt+ϕ))2=A2ω2cos2(ωt+ϕ)
α2=(−Aω2sin(ωt+ϕ))2=A2ω4sin2(ωt+ϕ)
- We know that cos2(θ)+sin2(θ)=1. Thus, we can express the relationship:
v2A2ω2+α2A2ω4=1
- Rearranging gives:
v2A2ω2+α2A2ω4=1
- Let x=α2 and y=v2:
yA2ω2+xA2ω4=1
- This is a linear equation in the form of yb+xa=1, which represents a straight line in the v2 vs α2 graph.
- The graph of v2 (on the Y-axis) versus α2 (on the X-axis) will be a straight line.
Topper's Solved these Questions
- OSCILLATIONS BOOK - TARGET PUBLICATIONCHAPTER - OSCILLATIONS EXERCISE - COMPETITIVE THINKING
135 Videos
- OSCILLATIONS BOOK - TARGET PUBLICATIONCHAPTER - OSCILLATIONS EXERCISE - EVALUATION TEST
14 Videos
- OSCILLATIONS BOOK - TARGET PUBLICATIONCHAPTER - OSCILLATIONS EXERCISE - EVALUATION TEST
14 Videos
- MODEL QUESTION PAPER BOOK - TARGET PUBLICATIONCHAPTER - MODEL QUESTION PAPER EXERCISE - MODEL QUESTION PAPER -II
47 Videos
- QUESTION PAPER 2019BOOK - TARGET PUBLICATIONCHAPTER - QUESTION PAPER 2019EXERCISE - MCQ
45 Videos
Similar Questions
A particle is performing a linear simple harmonic motion. If the instantaneous acceleration and velocity of the particle are a and v respectively, identify the graph which correctly represents the relation between a and v.
View SolutionIn a linear S.H.M., the acceleration of the particle is zero, when its velocity is
View Solution
Knowledge Check
A particle is performing a linear simple harmonic motion if the acceleration and the corresponding velocity of the particle are a and v respectively. Which of the following graph is correct?
A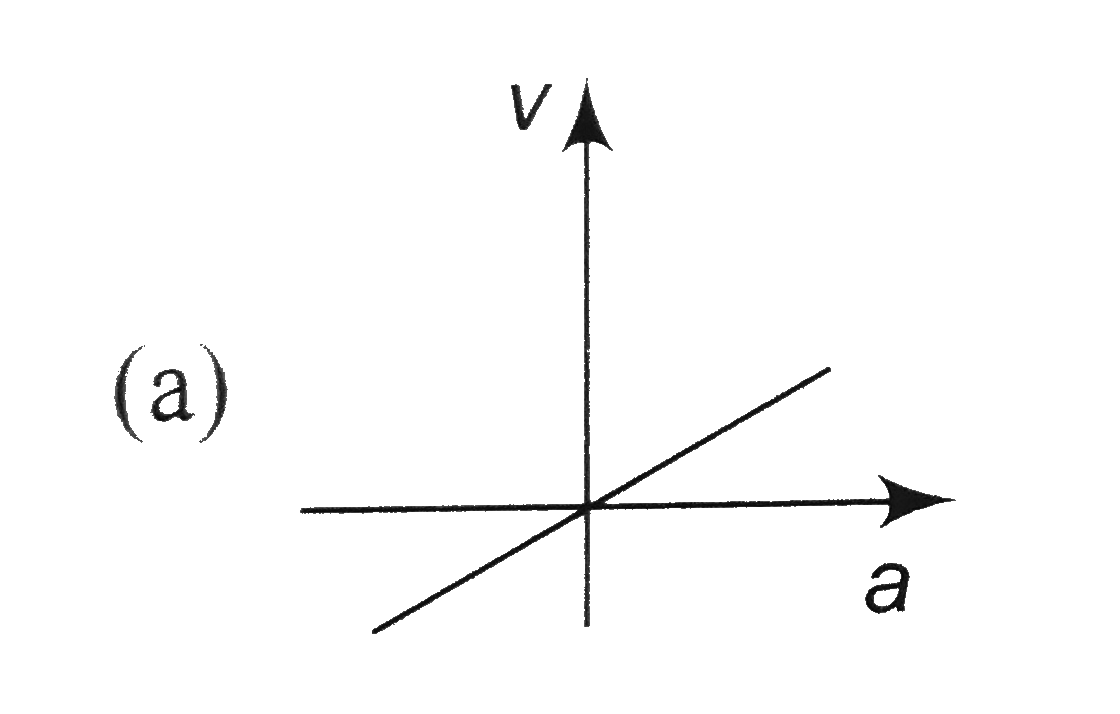 B
B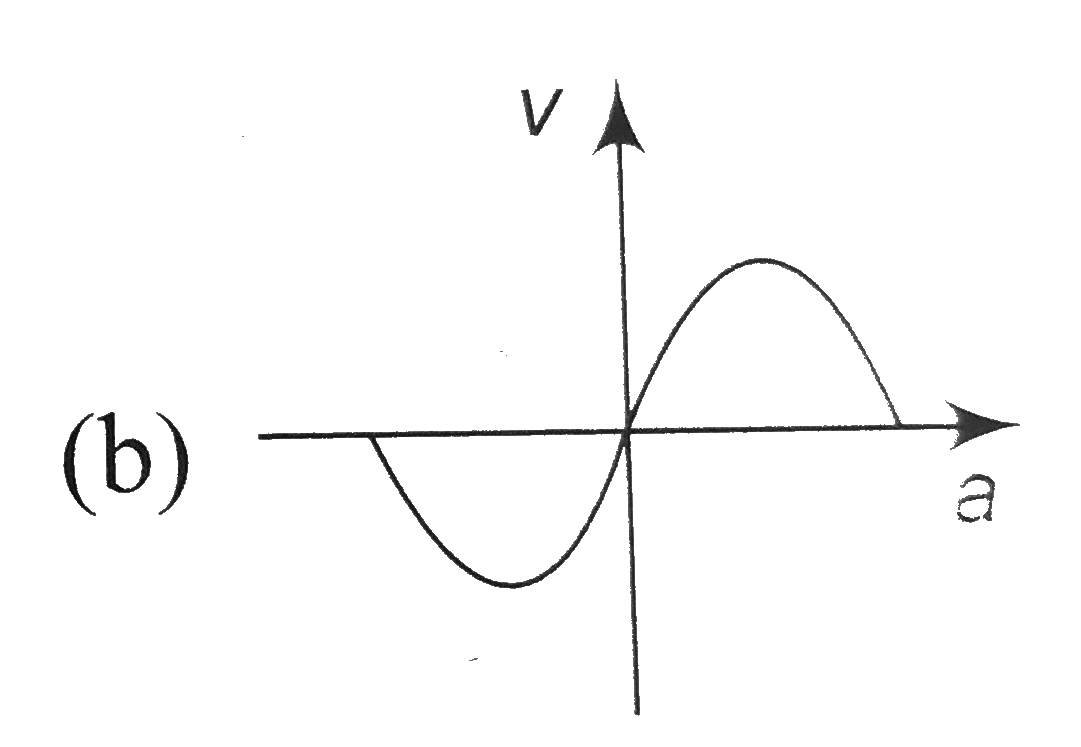 C
C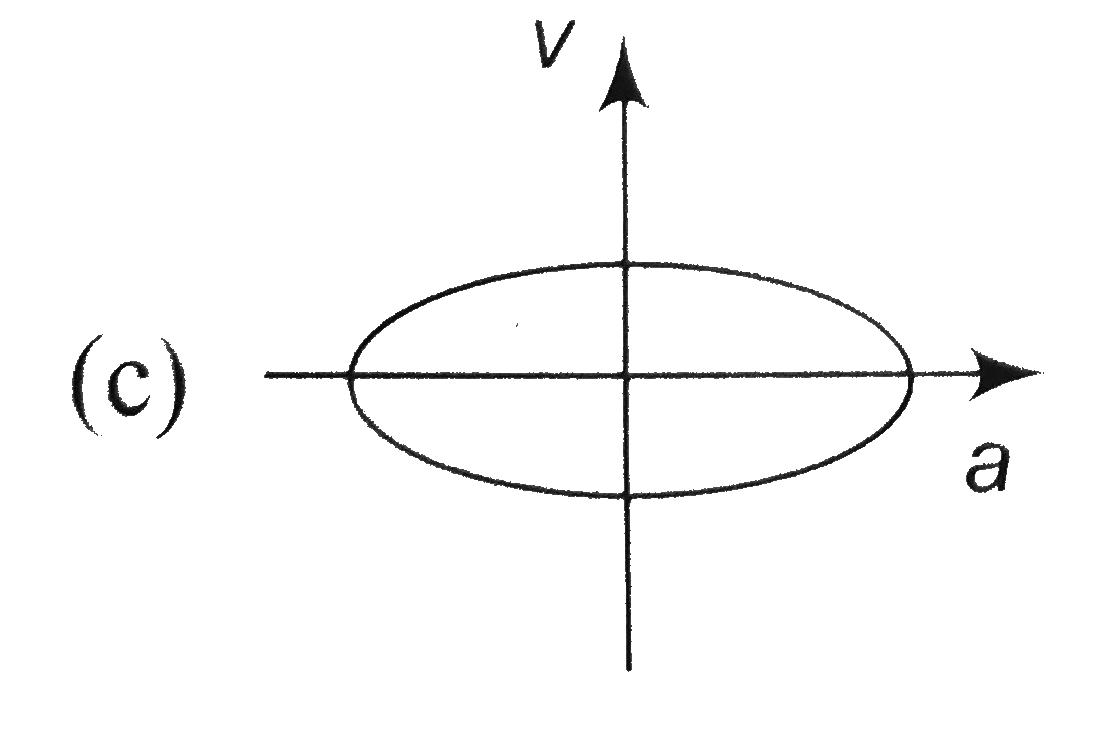 D
D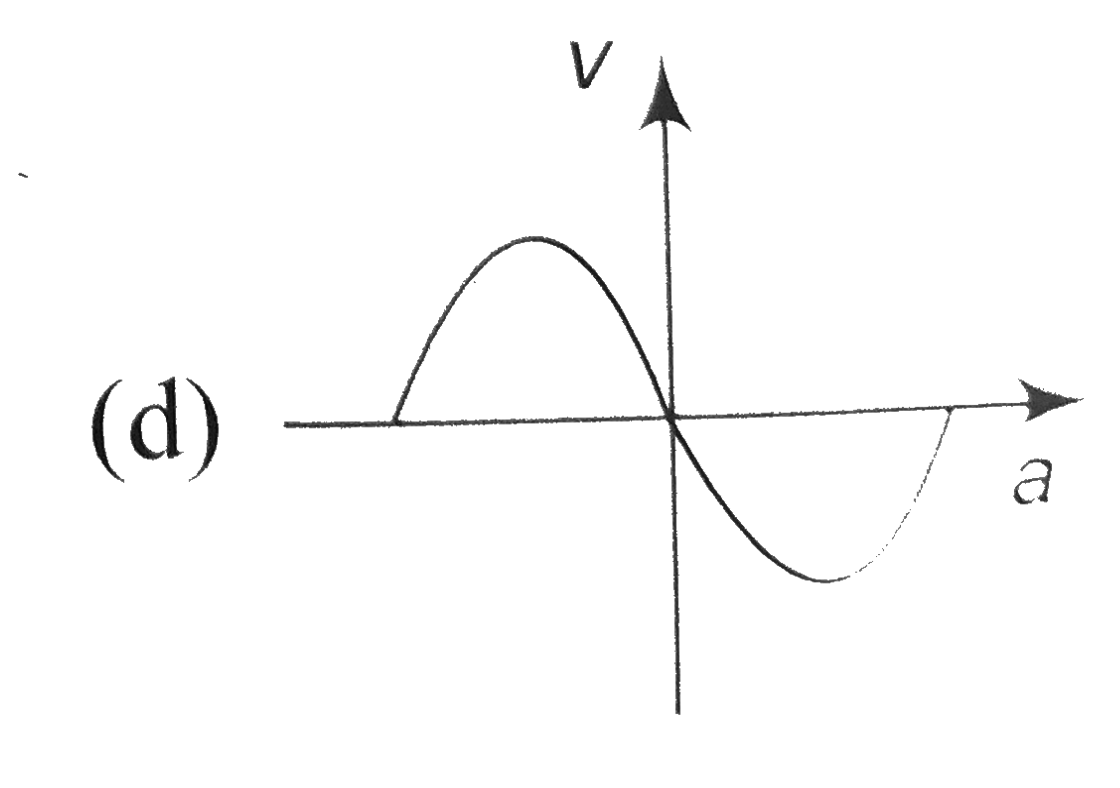
A particle is in a linear SHM. If acceleration and the corresponding velocity of this particle are a and v then the graph relating to these values is
A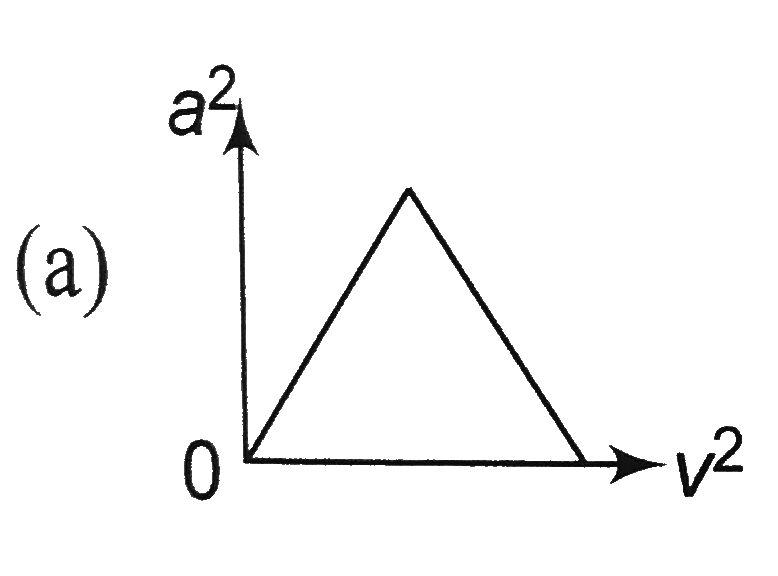 B
B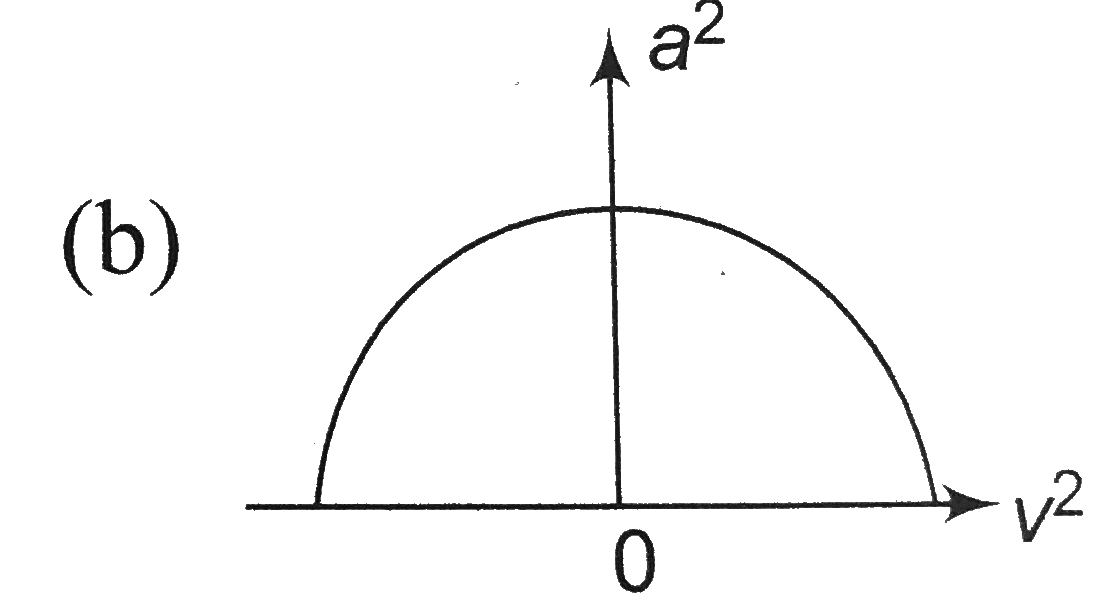 C
C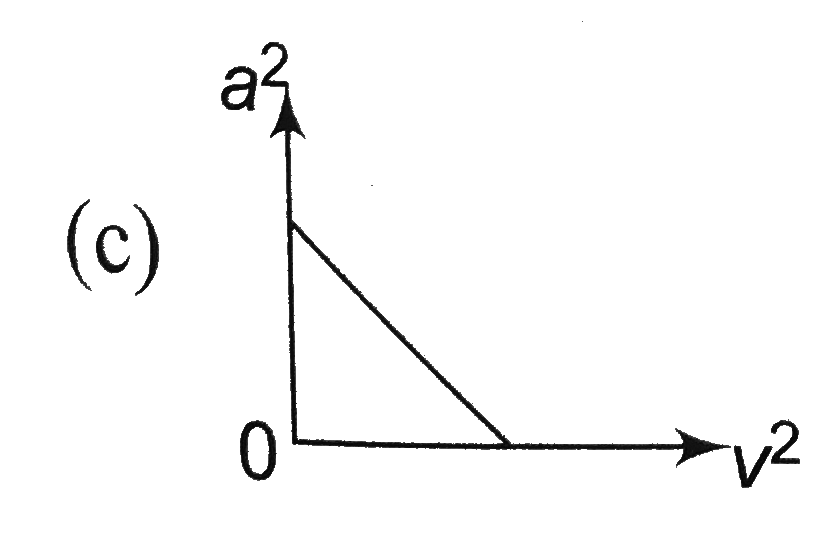 D
D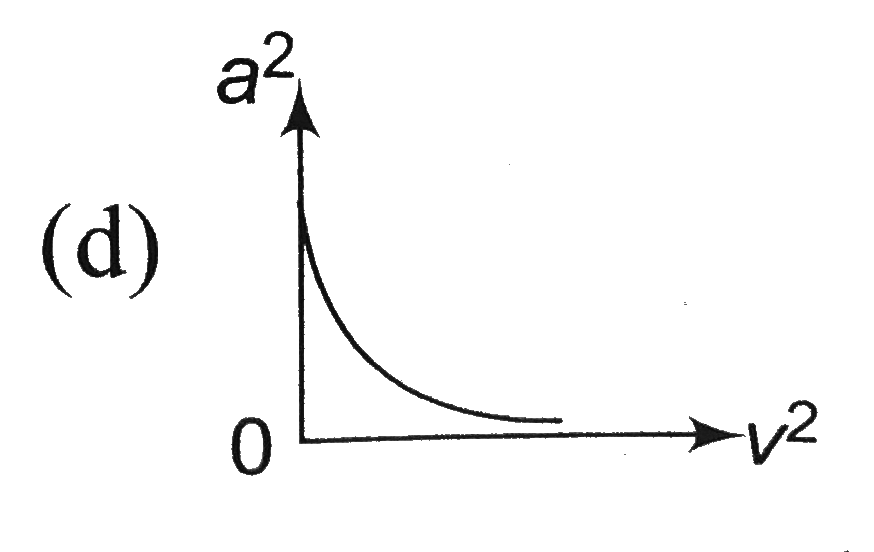
A particle performing S.H.M. about equilibrium position. Then the velocity of the particle is
Aslower from mean to extreme positionBfaster from mean to extreme positionCslower initial from mean position and faster lateral and stop at the endDfaster initil from mean position and later on falls off, suddenly
A mass M is performing linear simple harmonic motion. Then correct graph for acceleration a and corresponding linear velocity v is
View SolutionA particle is executing S.H.M.if v1 and v2 are the velocities of the particle at distances x1 and x2 from mean position respectively , then time period of oscillation is
View SolutionA particle is performing a linear S.H.M about the mean position with the equation of velocity given by 4v2−25−x2. Then the period of motion is
View SolutionA particle performs linear S.H.M. At a particular instant, velocity of the particle is 'u' and acceleration is '∝' while at another instant, velocity is 'v' and acceleration 'β' (0ltpropltbeta). The distance between the two position is
View SolutionWe draw the reference circle of a particle (M) performing a linear S.H.M. If the period of M is 2 sec, then the angular velocity of the reference particle will be
View Solution
