A wire of length L is hanging from a fixed support. The length changes to L1andL2 when masses M1andM2 are suspended respectively from its free end. Then L is equal to
L1+L22
√L1L2
L1M2+L2M1M1+M2
L1M2−L2M1M2−M1
The correct Answer is:D
To find the original length L of the wire when different masses M1 and M2 are suspended from its free end, we can use the relationship between the change in length of the wire and the applied force due to the weights of the masses.
1. Understanding the Problem:
- We have a wire of original length L.
- When mass M1 is suspended, the length of the wire becomes L1.
- When mass M2 is suspended, the length of the wire becomes L2.
2. Using Hooke's Law:
- The extension of the wire due to the weight of the mass can be expressed using Hooke's Law:
Extension=F⋅LA⋅Y
- Here, F is the force (weight of the mass), A is the cross-sectional area of the wire, and Y is the Young's modulus of the material.
3. Setting Up the Equations:
- For mass M1:
L1−L=M1g⋅LA⋅Y
- For mass M2:
L2−L=M2g⋅LA⋅Y
4. Rearranging the Equations:
- Rearranging both equations gives:
L=L1−M1g⋅LA⋅Y
L=L2−M2g⋅LA⋅Y
5. Equating the Two Expressions for L:
- Since both expressions equal L, we can set them equal to each other:
L1−M1g⋅LA⋅Y=L2−M2g⋅LA⋅Y
6. Simplifying the Equation:
- Rearranging gives:
L1−L2=(M1g−M2gA⋅Y)L
- This can be simplified to:
L=(L1−L2)A⋅Yg(M1−M2)
7. Final Expression for L:
- Thus, the original length L can be expressed as:
L=L1M2−L2M1M2−M1
Final Answer:
L=L1M2−L2M1M2−M1
- We have a wire of original length L.
- When mass M1 is suspended, the length of the wire becomes L1.
- When mass M2 is suspended, the length of the wire becomes L2.
- The extension of the wire due to the weight of the mass can be expressed using Hooke's Law:
Extension=F⋅LA⋅Y
- Here, F is the force (weight of the mass), A is the cross-sectional area of the wire, and Y is the Young's modulus of the material.
- For mass M1:
L1−L=M1g⋅LA⋅Y
- For mass M2:
L2−L=M2g⋅LA⋅Y
- Rearranging both equations gives:
L=L1−M1g⋅LA⋅Y
L=L2−M2g⋅LA⋅Y
- Since both expressions equal L, we can set them equal to each other:
L1−M1g⋅LA⋅Y=L2−M2g⋅LA⋅Y
- Rearranging gives:
L1−L2=(M1g−M2gA⋅Y)L
- This can be simplified to:
L=(L1−L2)A⋅Yg(M1−M2)
- Thus, the original length L can be expressed as:
L=L1M2−L2M1M2−M1
L=L1M2−L2M1M2−M1
Topper's Solved these Questions
- BOOK - TARGET PUBLICATIONCHAPTER - ELASTICITYEXERCISE - Evaluation test14videos
ELASTICITY
- BOOK - TARGET PUBLICATIONCHAPTER - ELASTICITYEXERCISE - Critical Thinking54videos
ELASTICITY
- BOOK - TARGET PUBLICATIONCHAPTER - CURRENT ELECTRICITY EXERCISE - Evaluation Test6videos
CURRENT ELECTRICITY
- BOOK - TARGET PUBLICATIONCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - EVALUATION TEST8videos
ELECTROMAGNETIC INDUCTION
Similar Questions
A wire of length L,area of cross section A is hanging from a fixed support. The length of the wire changes to L1 when mass M is suspended from its free end. The expression for Young's modulus is:
View SolutionThe value of tension in a long thin metal wire has been changed from T1 to T2. The lengths of the metal wire at two different values of tension T1 and T2 are l1andl2 respectively. The actual length of the metal wire is :
View Solution
Knowledge Check
- Question 1 - Select One
A wire of length L,area of cross section A is hanging from a fixed support. The length of the wire changes to L1 when mass M is suspended from its free end. The expression for Young's modulus is:
AMg(L1−L)ALBMgLAL1CMgLA(L1−L)DMgL1AL - Question 2 - Select One
The balancing lengths for the cells of e.m.f. E1 and E2 are l1 and l2 respectively. If they are connected separately then
AE1E2=l1l2BE1E2=l1+l2l1−l2CE1E2=l1+l2l2DE1E2=l1−l2l2 - Question 3 - Select One
A string of length L and mass M hangs freely from a fixed point. Then the velocity of transverse waves along the string at a distance x from the free end is
A√gLB√gxCgLDgx
The length of wire, when M1 is hung from it, is l1 and is l2 with both M1 and M2 hanging. The natural length of wire is :-
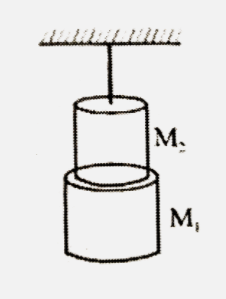 View Solution
View SolutionTwo point masses m1 and m2 are fixed to a light rod hinged at one end. The masses are at distances l1 and l2 repsectively from the hinge. Find the time period of oscillation (small amplitude) of this system in seconds if m1=m2,l1=1m,l2=3m. If the time period is xπ, then find x.
 View Solution
View SolutionWhen a thin iron wire of length l is heated from a temperature T1 to T2 , a change of 1% in its length is observed. The percentage change in area of iron plate of dimension 2l×l when it is heated from T1 to T2 is
View SolutionTwo wires of equal diameters, of resistivities ρ1 and ρ2 and length l1 and l2, respectively of the combination is
View SolutionA metal wire of length L is suspended vertically from a rigid support. When a bob of mass M is attached to the lower end of wire, the elongation of the wire is l:
View Solution

