Two rings having masses M and 2M respectively, having the same radius are placed coaxially as shown in the figure.
 If the mass distribution on both the rings is non-uniform, then the gravitational potential at point P is
If the mass distribution on both the rings is non-uniform, then the gravitational potential at point P is
−GMR[1√2+2√5]
−GMR[1+22]
zero
cannot be determined from given information
The correct Answer is:A
As all the point on the periphery of either ring are at same distance from point P, the potential at point P due to whole ring can be calculate as V=−(GM)/(√R2+x2) where x is axial distance from the centre of the ring. This expression is independent of the fact whether the distribution of mass is uniform or non-uniform.
So, V at P is V=−GM√2R−G×2M√5R
=−GMR[1√2+2√5].
Topper's Solved these Questions
- BOOK - NARAYNACHAPTER - GRAVITATIONEXERCISE - LEVEL-VI42videos
GRAVITATION
- BOOK - NARAYNACHAPTER - GRAVITATIONEXERCISE - ILLUSTRATION49videos
GRAVITATION
- BOOK - NARAYNACHAPTER - GRAVITATIONEXERCISE - LEVEL-II (H.W)32videos
GRAVITATION
- BOOK - NARAYNACHAPTER - FRICTIONEXERCISE - Passage type of questions I6videos
FRICTION
- BOOK - NARAYNACHAPTER - KINETIC THEORY OF GASESEXERCISE - LEVEL-III(C.W)52videos
KINETIC THEORY OF GASES
Similar Questions
Four rings each of mass M and radius R are arranged as shown in the figure. The moment of inertia of the system about YY' will be
 View Solution
View SolutionA rod of length / and of mass M and another rod of length 2/ and mass 2M are arranged as shown below in the figure.The magnitude of gravitational field at point P is
View Solution
Knowledge Check
- Question 1 - Select One
Three rings each of mass M and radius R are arranged as shown in the figure. The moment of inertia of the system about YY¢ will be
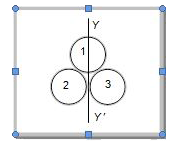 A3MR2B32MR2C5MR2D72MR2
A3MR2B32MR2C5MR2D72MR2 - Question 2 - Select One
A mass m is placed in the cavity inside hollow sphere of mass M as shown in the figure. The gravitational force on m is
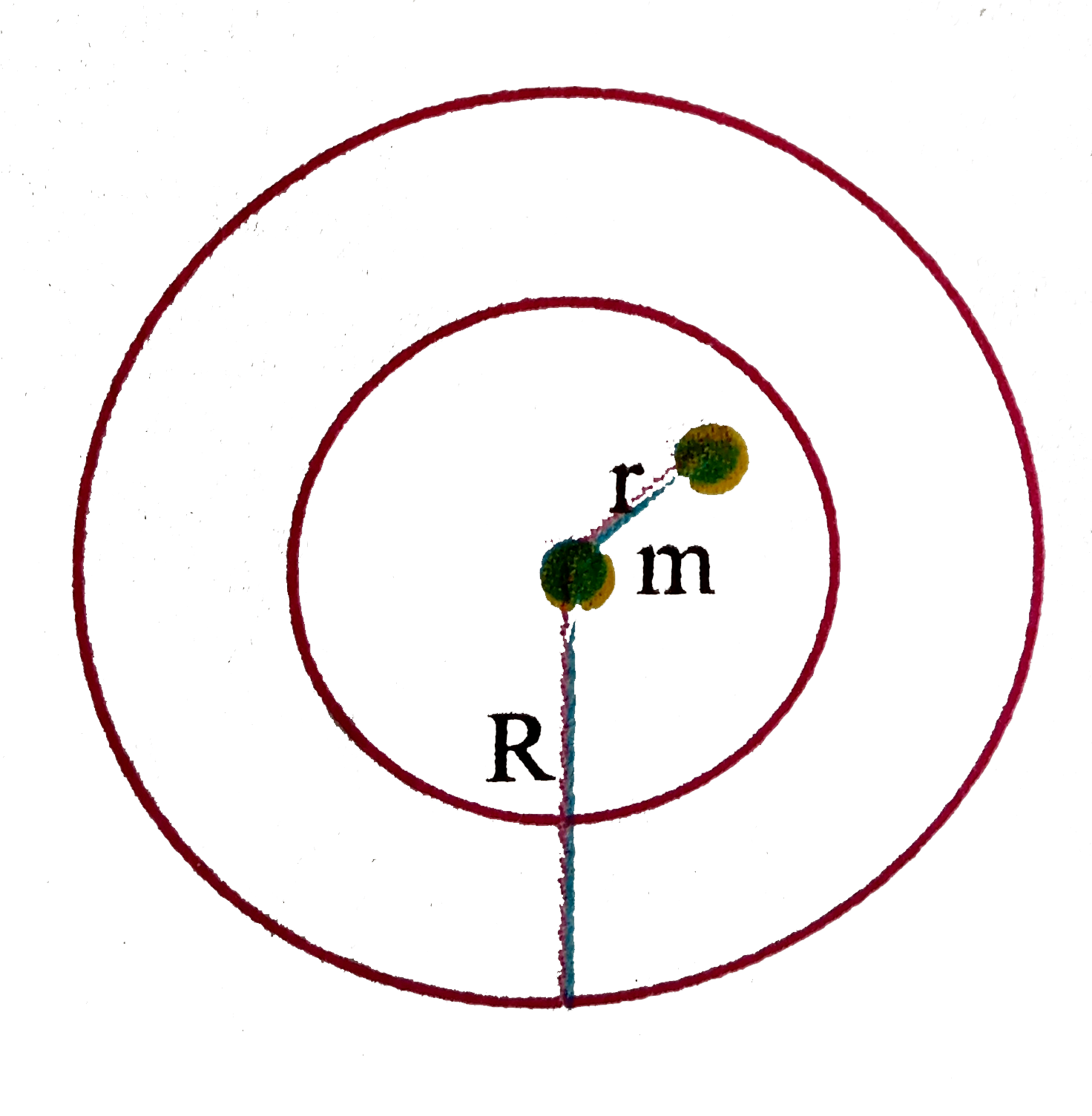 AGMmR2BGMmr2CGMm(R−r)2Dzero
AGMmR2BGMmr2CGMm(R−r)2Dzero - Question 3 - Select One
A mass m is placed at point P lies on the axis of a ring of mass M and radius R at a distance R from its centre. The gravitational force on mass M is
AGMm√2R2BGMm2R2CGMm2√2R2DGMm4R2
A ring of mass M and radius R lies in x−y plane with its centre at origin as shown. The mass distribution of ring is non uniform such that, at any point P on the ring, the mass per unit length is given by λ=λ0cos2θ (where λ0 is a positive constant). Then the moment of inertia of the ring about z-axis is :
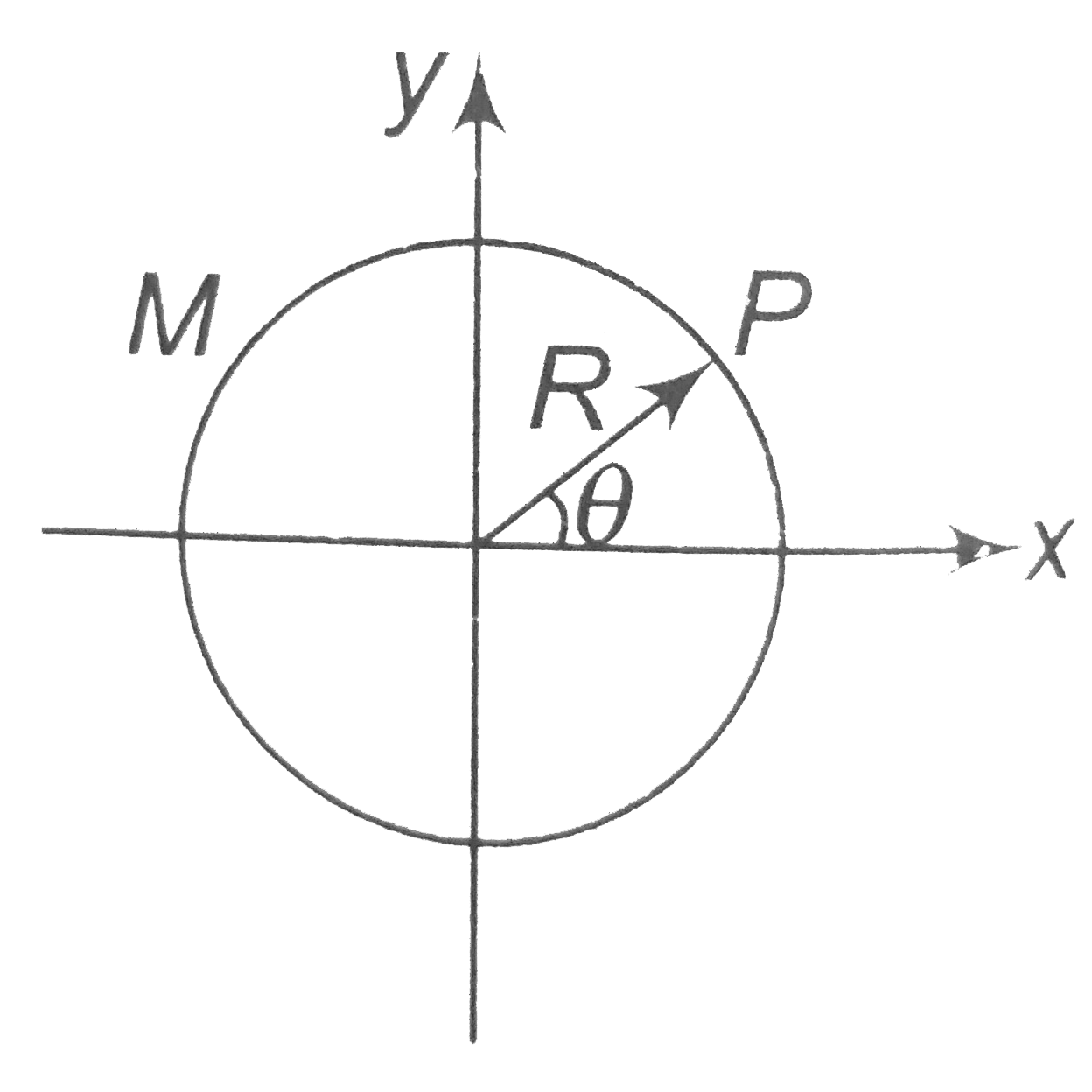 .View Solution
.View SolutionTwo identical concentric rings each of mass m and radius R are placed perpendicularly. What is the moment of inertia of the system about the axis of one of the rings ?
View SolutionFigure (a) shows a ring of mass m and figure (b) shows half portion of the same ring . Gravitational field at point P in figure (b) is I2 in magnitude and makes an angle ϕ with line . AB. Gravitational field at point P in figure (a) is I1 in magnitude . The ratio of I12I2 is
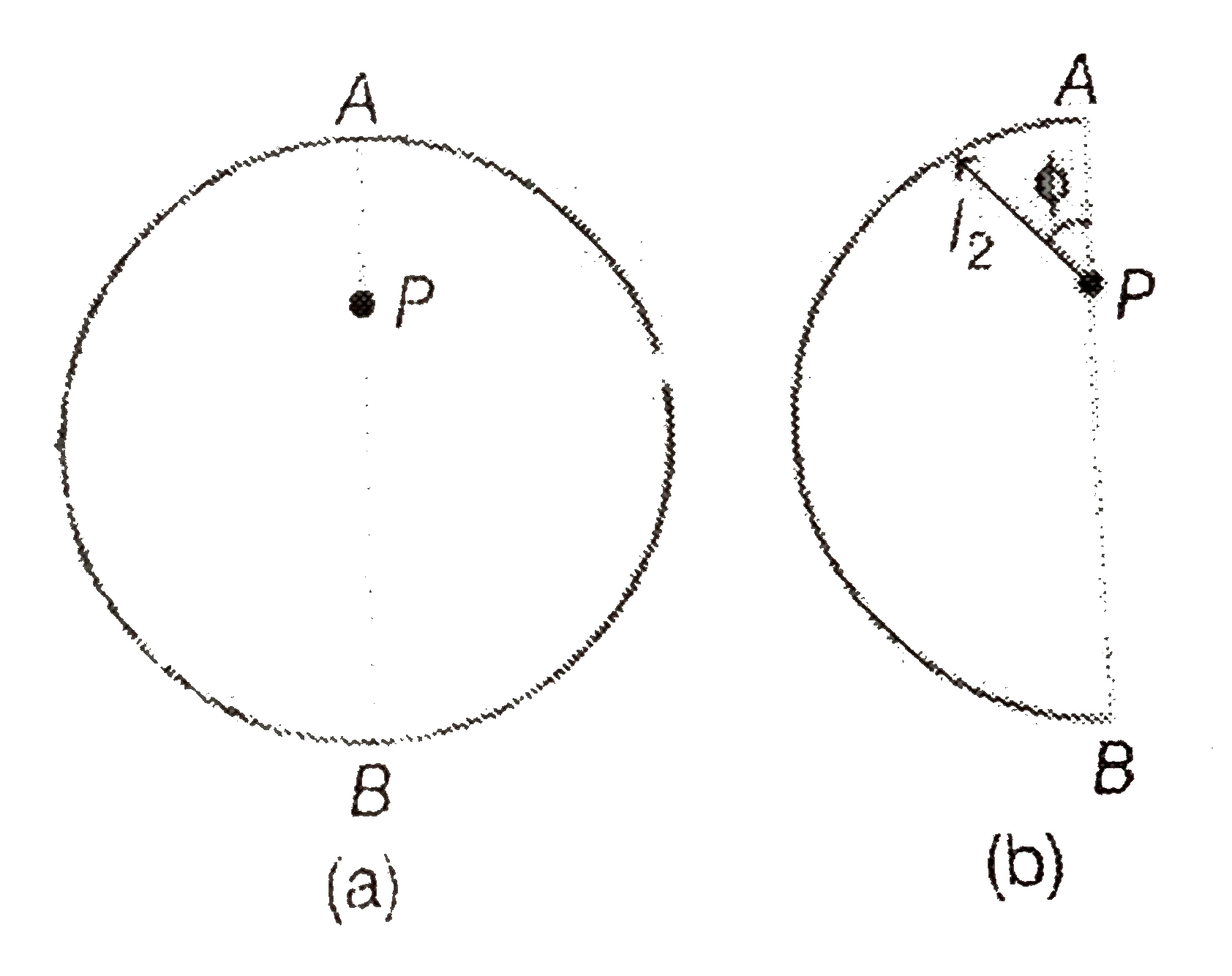 View Solution
View SolutionThree rings each of mass m and radius r are so placed that they touch each other. The radius of gyration of the system about the axis as shown in the figure is
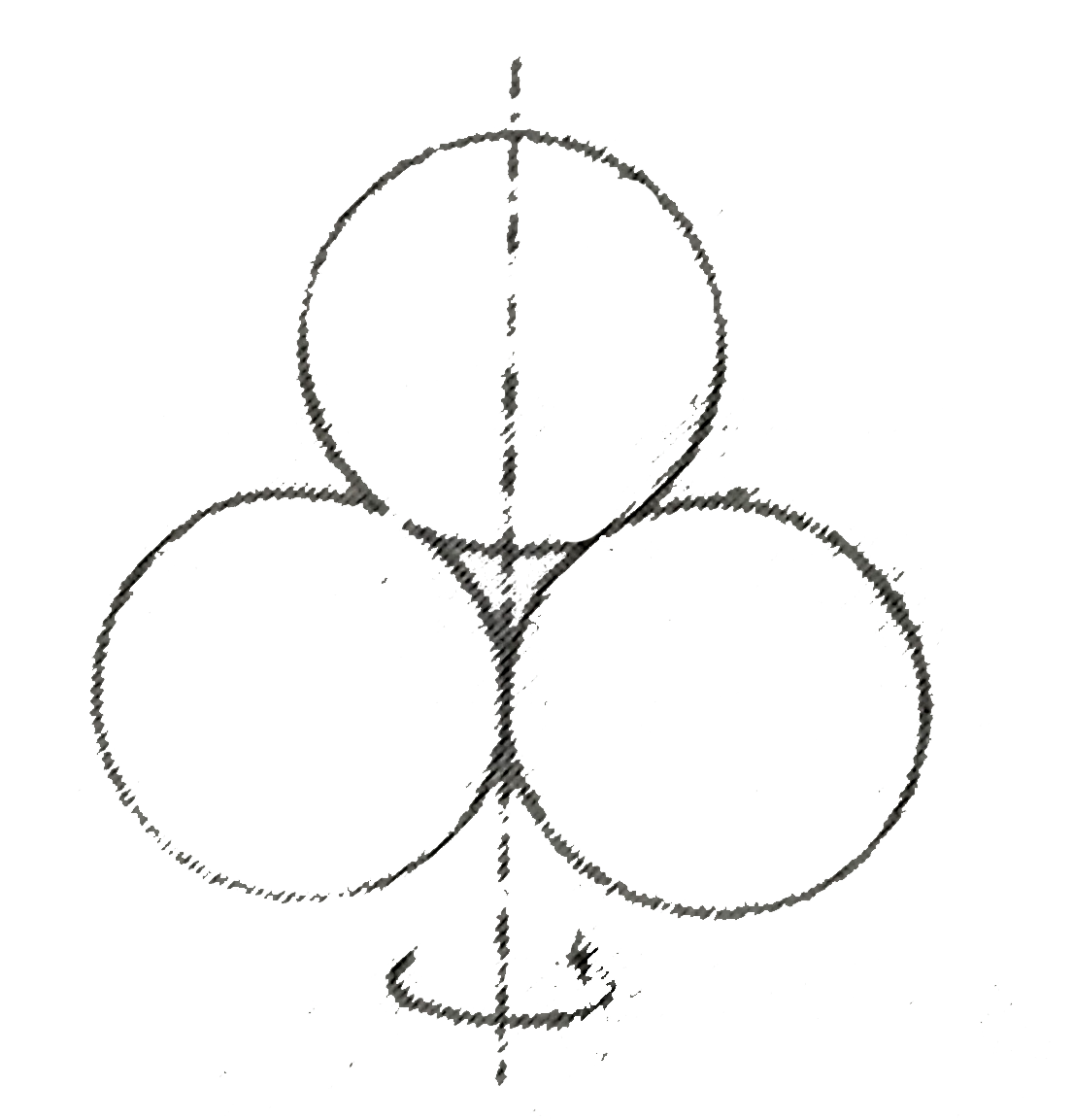 View Solution
View SolutionA uiform ring of mass M and radius R is placed directly above a uniform sphere of mass 8M and same radius R. The centre of the sphere. The gravitational atraction between the sphere and the ring is
View Solution

