A satellite is orbiting around earth in a circular orbit of radius $r$ . A particle of mass $m$ is projected from satellite in forward direction with velocity $v = \sqrt{\frac{2}{3}}$ times orbital velocity (this velocity is with respect to the earth). During subsequent motion of the particle, its minimum distance from the centre of earth is

A

$\frac{r}{2}$

B

$r$

C

$\frac{2 r}{3}$

D

$\frac{4 r}{3}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A

As the velocity of particle is less than orbital velocity of satellite, the particle goes in elliptical orbit semimajor axis less then $r$ .

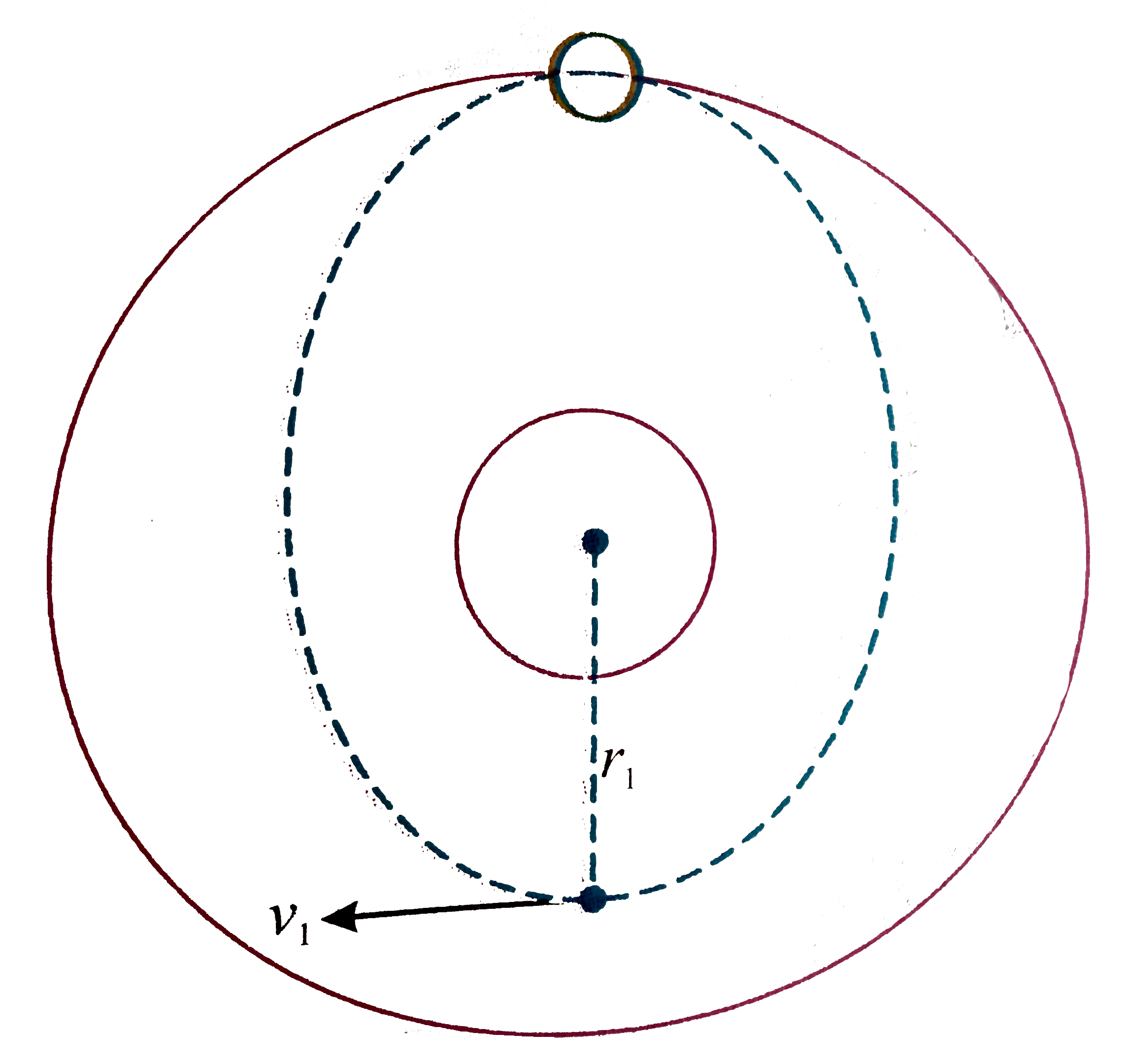
Let $r_{1}$ be the maximum distance and $v_{1}$ be velocity of particle at this position, then $m_{0} \times \sqrt{\frac{2}{3}} \times v_{0} r = m_{0} v_{1} r_{1}$ , where $m_{0}$ is the mass of particle and $v_{0}$ is orbital speed equal to
$\sqrt{\frac{G M}{r}} \Rightarrow v_{1} r_{1} = \sqrt{\frac{2}{3}} v_{0} r$
From energy conservation,
$\frac{m_{0} \times 2 / 3 v_{0}^{2}}{2} - \frac{G M m_{0}}{r} = \frac{m_{0} v_{1}^{2}}{2} - \frac{G M m_{0}}{r_{1}}$
Solving above equations, we get $r_{1} = \frac{r}{2}$ .

|

Updated on:21/07/2023

Class 11 PHYSICS GRAVITATION

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
A satellite is orbiting around the earth in a circular orbit of radius $r$ . A particle of mass $m$ is projected from the satellite in a forward direction with a velocity $v = 2 / 3$ times the orbital velocity (this velocity is given w.r.t. earth). During subsequent motion of the particle, its minimum distance from the centre of earth is
A $\frac{r}{2}$
B $r$
C $\frac{2 r}{3}$
D $\frac{4 r}{5}$
Question 2 - Select One
A satellite is orbiting the earth in a circular orbit of radius $r$ . Its
Akinetic energy veries as $r$
Bangular momentum varies as $r^{- 1}$
Clinear momentum varies as $r^{2}$
Dfrequency of revolution varies as $r^{- 3 / 2}$
Question 3 - Select One
A satellite is revolving in circular orbit of radius $r$ around the earth of mass M. Time of revolution of satellite is
A $T \propto \frac{r^{5}}{G M}$
B $T \propto \sqrt{\frac{r^{3}}{G M}}$
C $T \propto \sqrt{\frac{r}{\frac{G M^{2}}{3}}}$
D $T \propto \sqrt{\frac{r^{3}}{\frac{G M}{4}}}$

NARAYNA-GRAVITATION-LEVEL-V

Home
Ask Doubt
Profile