What are the units of K14π∈0 ?
C2N−1m−2
C−2N−1m2
C2N1m2
unitless
The correct Answer is:B
To find the units of K=14πϵ0, we can follow these steps:
Step 1: Understand the context
The constant ϵ0 is known as the permittivity of free space, and it plays a crucial role in electromagnetism, particularly in Coulomb's law, which describes the force between two point charges.
Step 2: Recall the formula for electric force
Coulomb's law states that the electric force F between two point charges q1 and q2 separated by a distance r is given by:
F=14πϵ0q1q2r2
From this equation, we can see that the term 14πϵ0 has units that must balance the units of force and the charges involved.
Step 3: Identify the units of force
The unit of force F is the Newton (N). In terms of base units, we have:
1N=1kg⋅m/s2=M⋅L⋅T−2
Step 4: Identify the units of charge
The unit of charge in the SI system is the Coulomb (C).
Step 5: Write the units of ϵ0
From the equation of Coulomb's law, we can rearrange it to express ϵ0:
ϵ0=q1q2F⋅r2
Thus, the units of ϵ0 can be derived as follows:
- The units of q1 and q2 are Coulombs (C).
- The units of F are Newtons (N).
- The units of r2 are m2 or L2.
So, the units of ϵ0 can be expressed as:
Units of ϵ0=C2N⋅m2=C2M⋅L⋅T−2⋅L2=C2M⋅L3⋅T−2
Step 6: Find the units of 1ϵ0
Taking the reciprocal gives us:
Units of 1ϵ0=M⋅L3⋅T−2C2
Step 7: Determine the units of K=14πϵ0
Since 4π is a dimensionless constant, the units of K are the same as the units of 1ϵ0:
Units of K=M⋅L3⋅T−2C2
Final Answer
Thus, the units of K=14πϵ0 are:
M⋅L3⋅T−2⋅C−2
---
The constant ϵ0 is known as the permittivity of free space, and it plays a crucial role in electromagnetism, particularly in Coulomb's law, which describes the force between two point charges.
Coulomb's law states that the electric force F between two point charges q1 and q2 separated by a distance r is given by:
F=14πϵ0q1q2r2
From this equation, we can see that the term 14πϵ0 has units that must balance the units of force and the charges involved.
The unit of force F is the Newton (N). In terms of base units, we have:
1N=1kg⋅m/s2=M⋅L⋅T−2
The unit of charge in the SI system is the Coulomb (C).
From the equation of Coulomb's law, we can rearrange it to express ϵ0:
ϵ0=q1q2F⋅r2
Thus, the units of ϵ0 can be derived as follows:
- The units of q1 and q2 are Coulombs (C).
- The units of F are Newtons (N).
- The units of r2 are m2 or L2.
Units of ϵ0=C2N⋅m2=C2M⋅L⋅T−2⋅L2=C2M⋅L3⋅T−2
Taking the reciprocal gives us:
Units of 1ϵ0=M⋅L3⋅T−2C2
Since 4π is a dimensionless constant, the units of K are the same as the units of 1ϵ0:
Units of K=M⋅L3⋅T−2C2
Thus, the units of K=14πϵ0 are:
M⋅L3⋅T−2⋅C−2
Topper's Solved these Questions
- BOOK - NARAYNACHAPTER - UNITS AND MEASUREMENTSEXERCISE - LEVEL-I (C.W)42videos
UNITS AND MEASUREMENTS
- BOOK - NARAYNACHAPTER - UNITS AND MEASUREMENTSEXERCISE - LEVEL-II (C.W)28videos
UNITS AND MEASUREMENTS
- BOOK - NARAYNACHAPTER - UNITS AND MEASUREMENTSEXERCISE - STATEMENT TYPE QUESTION23videos
UNITS AND MEASUREMENTS
- BOOK - NARAYNACHAPTER - TRANSMISSION OF HEATEXERCISE - LEVEL-II(C.W)27videos
TRANSMISSION OF HEAT
- BOOK - NARAYNACHAPTER - VECTORSEXERCISE - LEVEL-II (H.W)14videos
VECTORS
Similar Questions
Knowledge Check
- Question 1 - Select One
What are the unit of μ04π
ANA−1m2BNA−2CNm2C2Dunitless - Question 2 - Select One
In coulomb's law, constant of proportional K=14π∈0 has units
ANBN−m2CNm2C2DN−m2m2 - Question 3 - Select One
A point charge 'Q' is placed at the centre of a spherical cavity of radius 'b' carved inside a solid conducting sphere of radius 'a'. Then total energy of the system is:
[k=14π∈0]
 AKQ22a−kQ22bBkQ22a+kQ22bCkQ2a+kq2bDkQ2a−kQ2b
AKQ22a−kQ22bBkQ22a+kQ22bCkQ2a+kq2bDkQ2a−kQ2b
A sphere of radius R contains charge density ρ(r)=A(R−r), for 0<r<R. The total electric charge inside the sphere is Q.
The electric outside the sphere is (k=14π∈0)View SolutionAn infinite number of charges each equal to q are placed along the x-axis at x=1m,x=2m,x=4m,x=8m, ... and so on. Find the potential and electric field at the point x = 0 due to this set of charges. What will be potential and electric field ifin the above set up if the consecutive charge have opposite sign?
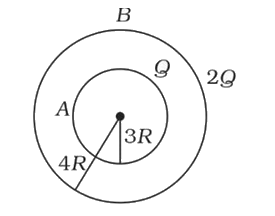
[q2π∈0,q3π∈0,q6π∈0,q5π∈0]View SolutionIn the figure shown, conducting shells A and B have charges Q and 2Q distributed uniformly over and B. Value of VA−VB k is kQnR. Find n(k=14π∈0
 View Solution
View SolutionDetermine electric field at point P or O in the following cases , take 14π∈0.Qd2=E0.
(a)
(b)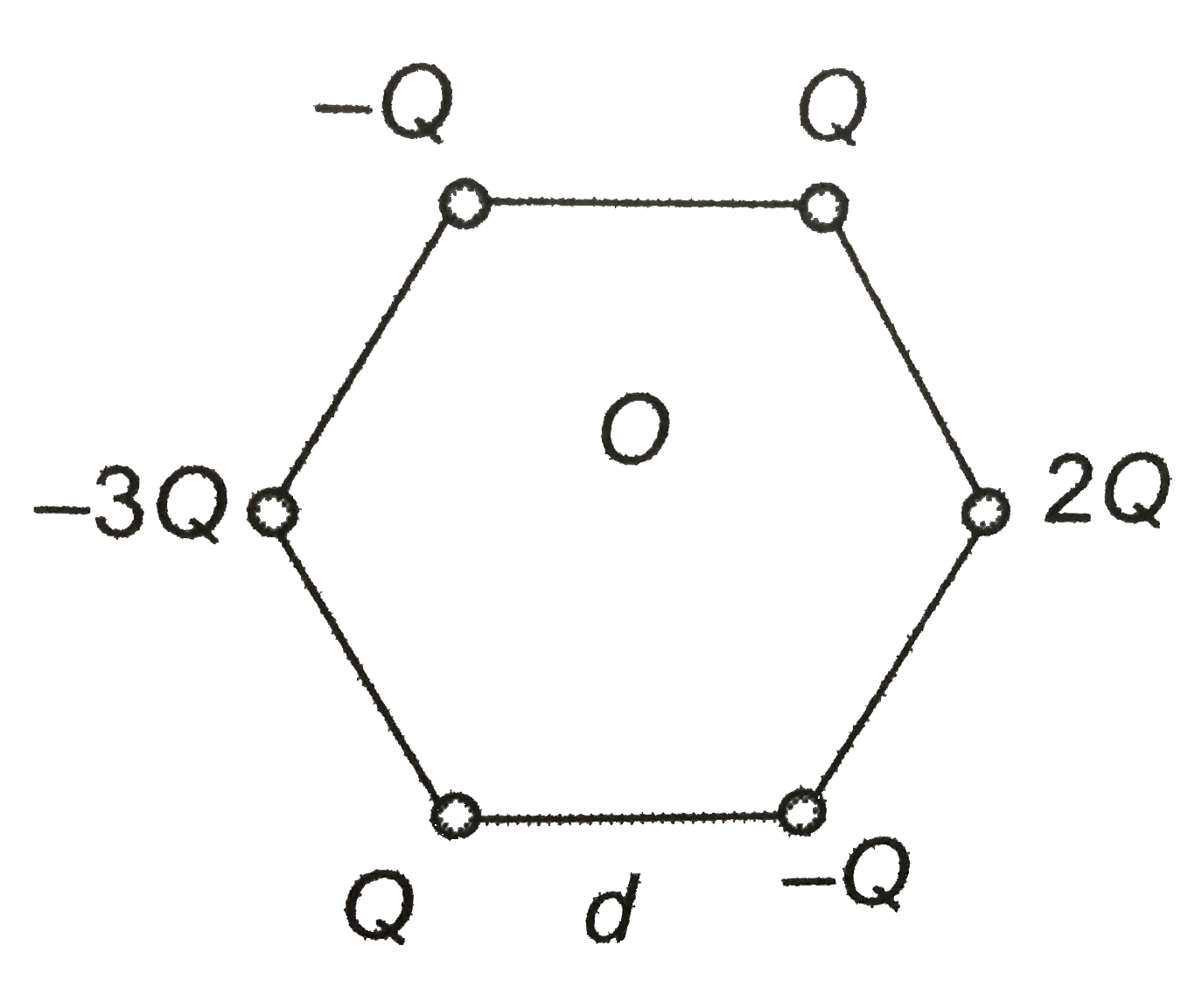 View Solution
View SolutionThe total flux associated with given cube will be - where 'a' is side of cube :-
(1∈0=4π×9×109)
 View Solution
View Solution