In $u - v$ method, we require the distance between object or image from the pole (vertex) of the mirror (actual distance). But practically we measure the distance between the indices $A$ and $B$ . (Observed distance). Which need not exactly co-inside with object and pole, there can be a slight mismatch called index error, which will be constant for every observation.

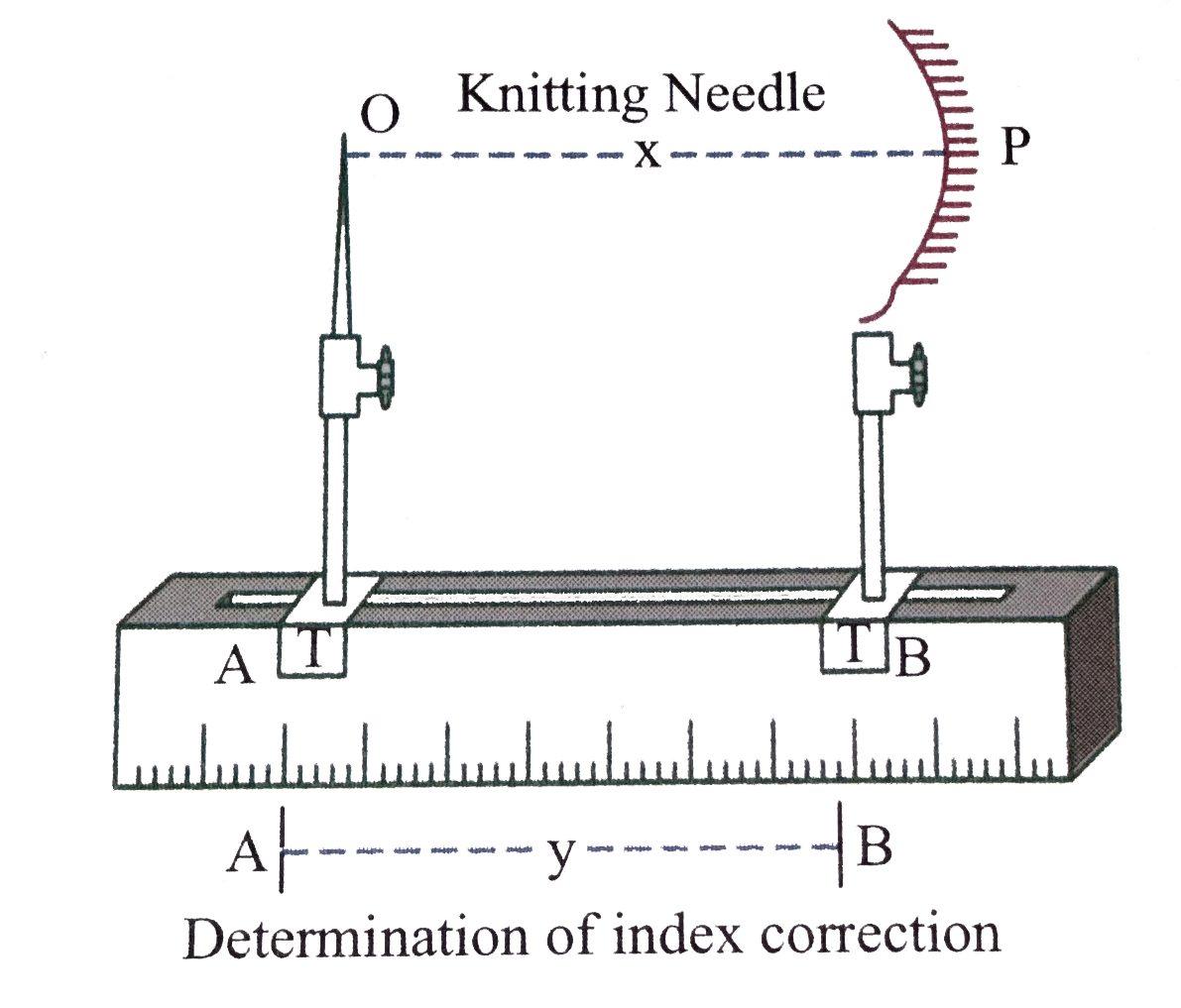
Index error=Observed distance-Actual distance(Just like zero error in screw guage, it is the excess reading).
To determine index error, mirror and object needle and placed at arbitary position. For measuring actual distance, a knitting needle is just fitted between the pole of mirror and object needle $O$ . The length of knitting needle will give the actual object distance while the seperation between indices $A$ and $B$ at that instant is the observed distance.
So index error is-
$e =$ Observed distance-Actual distance
$=$ Separation between indices $A$ and $B$ - Length of knitting neddle once we get $e$ , in
every observation, we get
Actual distance=Observed distance (separation between the indices)- Excess reading(e) There is an another term, Index corraction which is invert of index error.
Index correction=-index error
To find index error for $v$ , when the same knitting needle is adjusted between the pole and the image needle, the separation between the indices of image needle and mirror was found to be $19.9 c m$ . Index error for $v$ is

$0.1 c m$

$- 0.1 c m$

$0.2 c m$

$- 0.2 c m$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:B

$e = 19.9 c m - 20.0 c m = - 0.1 c m$

Updated on:21/07/2023

Class 12 PHYSICS EXPERIMENTAL PHYSICS

Topper's Solved these Questions

Knowledge Check

Question 1 - Select One
In $u - v$ method, we require the distance between object or image from the pole (vertex) of the mirror (actual distance). But practically we measure the distance between the indices $A$ and $B$ . (Observed distance). Which need not exactly co-inside with object and pole, there can be a slight mismatch called index error, which will be constant for every observation.

Index error=Observed distance-Actual distance(Just like zero error in screw guage, it is the excess reading).
To determine index error, mirror and object needle and placed at arbitary position. For measuring actual distance, a knitting needle is just fitted between the pole of mirror and object needle $O$ . The length of knitting needle will give the actual object distance while the seperation between indices $A$ and $B$ at that instant is the observed distance.
So index error is-
$e =$ Observed distance-Actual distance
$=$ Separation between indices $A$ and $B$ - Length of knitting neddle once we get $e$ , in
every observation, we get
Actual distance=Observed distance (separation between the indices)- Excess reading(e) There is an another term, Index corraction which is invert of index error.
Index correction=-index error
To find index error for $u$ , when a knitting needle of length $20.0 c m$ is adjusted between pole and object needle, the sepertion between the indices of object needle and mirror was observed to be $20.2 c m$ . Index corraction for u is
A $- 0.2 c m$
B $0.2 c m$
C $- 0.1 c m$
D $0.1 c m$
Question 2 - Select One
To find index error v when the same knitting needle is adjusted between the pole and the image needle the separation between the indices of image needle and mirror was found to be $19.9 c m$ Index error for v is .
A $0.1 c m$
B $- 0.1 c m$
C $0.2 c m$
D $- 0.2 c m$
Question 3 - Select One
In $u - v$ method, we require the distance between object or image from the pole (vertex) of the mirror (actual distance). But practically we measure the distance between the indices $A$ and $B$ . (Observed distance). Which need not exactly co-inside with object and pole, there can be a slight mismatch called index error, which will be constant for every observation.

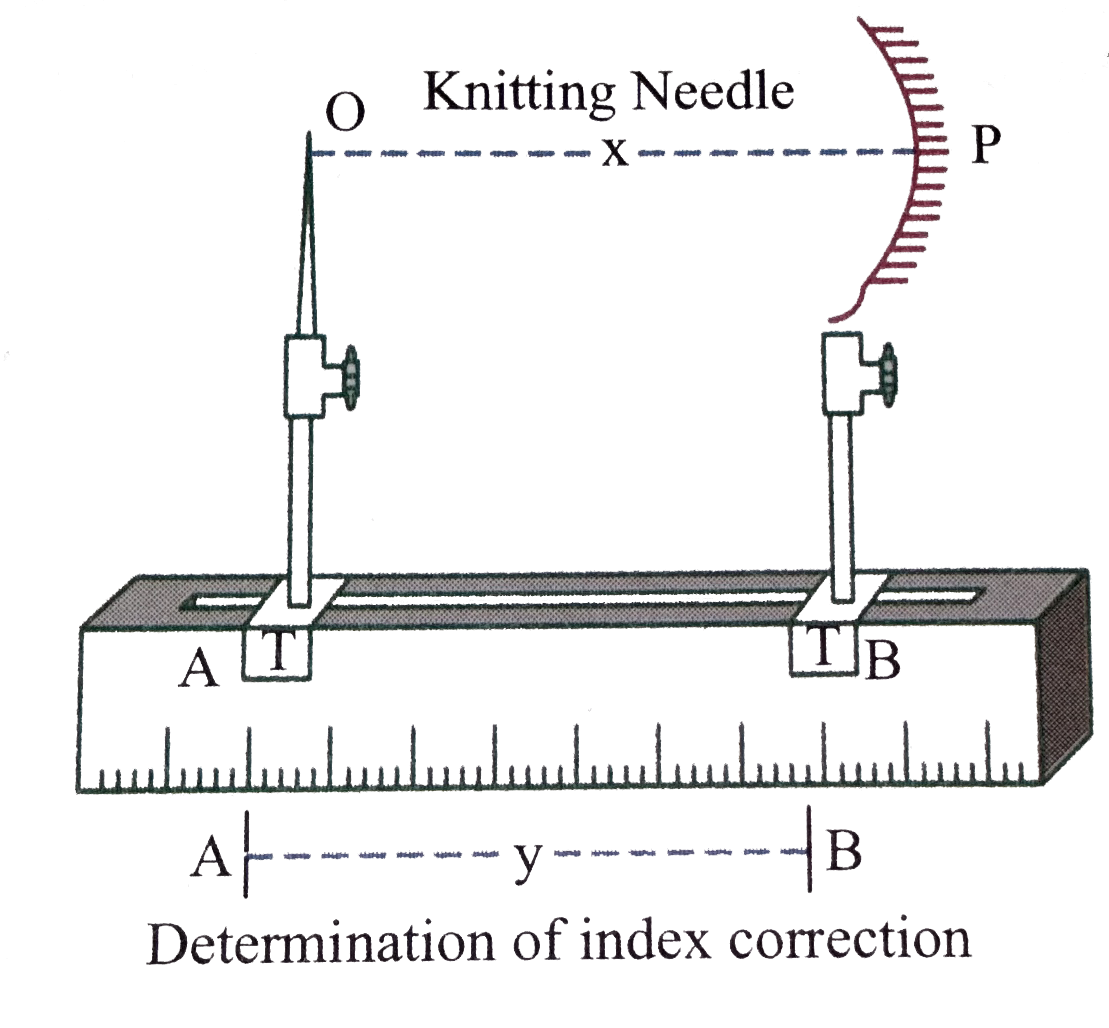
Index error=Observed distance-Actual distance(Just like zero error in screw guage, it is the excess reading).
To determine index error, mirror and object needle and placed at arbitary position. For measuring actual distance, a knitting needle is just fitted between the pole of mirror and object needle $O$ . The length of knitting needle will give the actual object distance while the seperation between indices $A$ and $B$ at that instant is the observed distance.
So index error is-
$e =$ Observed distance-Actual distance
$=$ Separation between indices $A$ and $B$ - Length of knitting neddle once we get $e$ , in
every observation, we get
Actual distance=Observed distance (separation between the indices)- Excess reading(e) There is an another term, Index corraction which is invert of index error.
Index correction=-index error
In some observation, the observed object distance (Separation between indices of object needle and mirror) is $30.2 c m$ , and the observed image distance is $19.9 c m$ . Using index correction from previous two equations, estimate the focal distance of the concave mirror!
A $36 c m$
B $20 c m$
C $12 c m$
D $8 c m$