Figure shows an electrical calorimeter to determine specific heat capacity of an unknown liquid, First of all, the mass of empty calorimeter (a copper container) is measured and suppose it is m1. Then the unknown liquid is poured in it. Now the combined mass of calorimeter+liquid system is measured and let it be m2. So the mass of liquid is (m2−m1). Initially both were at room temperature (θ0).
Now a heater is immeresed in if for time interval t. The voltage drop across the heater is V and current passing through it is I. Due to heat supplied, the temperature of both the liquid and calorimeter will rise simultaneously. After tsec, heater was switched off, and final temperature is θr. If there is no heat loss to surroundings. Heat supplied by the heater=Heat absorbed by the liquid+heat absorbed by the calorimeter (VI)t=(m2−m1)S1(θf−θ0)+m1Sc(θf−θ0)
The specific heat of the liquid S1=(VI)tθf−θ0−m1Sc(m2−m1)
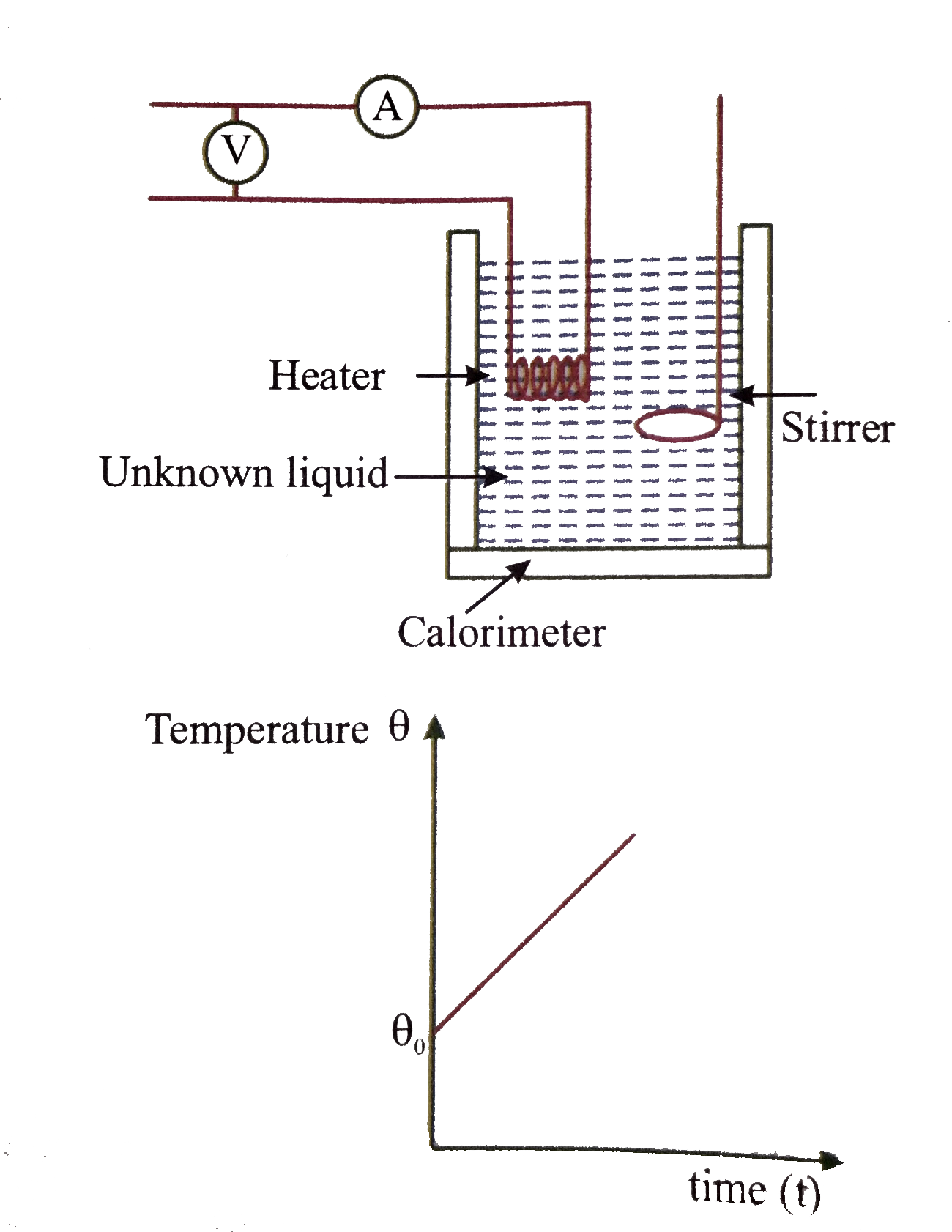
Radiation correction: There can be heat loss to environment. To compensate this loss, a correction is introduced.
Let the heater was on for tsec, and then it is switched off. Now the temperature of the mixture falls due to heat loss to environment. The temperature of the mixture is measured t/2sec. after switching off. Let the fall in temperature during this time is ɛ
Now the corrected final temperature is taken as θf=θf+ɛ
If mass and specific heat capacity of calorimeter is negligible, what would be maximum permissible error in Sl. Use the date mentioned below.
m1→, Sl→0, m2=1.00kg,
V=10.0V, I=10.0A,
t=1.00×102sec, θ0=15∘C,
Corrected θ1=65∘C
4%
5%
8%
12%
The correct Answer is:C
If m1→0, Sl→0, Sl=VItm2(θf−θ0)
dSlSl=ΔVV+ΔII+Δtt+Δm2m2+Δθr+Δθ0θr−θ0
=0.110.0+0.110.0+0.01×1021.00×102+0.011.00+1+150=8%
Topper's Solved these Questions
- EXPERIMENTAL PHYSICSBOOK - NARAYNACHAPTER - EXPERIMENTAL PHYSICSEXERCISE - Asserson and Reason
4 Videos
- EXPERIMENTAL PHYSICSBOOK - NARAYNACHAPTER - EXPERIMENTAL PHYSICSEXERCISE - Subjective type
6 Videos
- EXPERIMENTAL PHYSICSBOOK - NARAYNACHAPTER - EXPERIMENTAL PHYSICSEXERCISE - Multiple answer
6 Videos
- ELECTROSTATICS AND GAUSS LAWBOOK - NARAYNACHAPTER - ELECTROSTATICS AND GAUSS LAWEXERCISE - Intergers type question
11 Videos
- MAGNETISMBOOK - NARAYNACHAPTER - MAGNETISMEXERCISE - LEVEL-II (H.W)
24 Videos
Similar Questions
Assertion (A): Least count of all screw based instruments is same.
Reason (R ): Least count for all screw based instruments are found using the ratio of pitch per division of circular scale.
View SolutionA screw gauge having 100 equal division and a pitch of length 1mm is used to measue the diameter of a wire of length 5.6cm. The main scale reading is 1mmand47th circular division coincides with the scale. Find the curved surface area of wire in cm2 to appropriate significant fihure.
(useπ=227
View SolutionWhile finding specific heat capacity using calorimeter, error might occur due to:
View Solutiona unifrom surface charge density 8σ exists over the entire x−y plane except for a circular hole of radius of a point p(0,0,√3) on the z-axis is found to be 2√xσε0 ,Find the value of x.
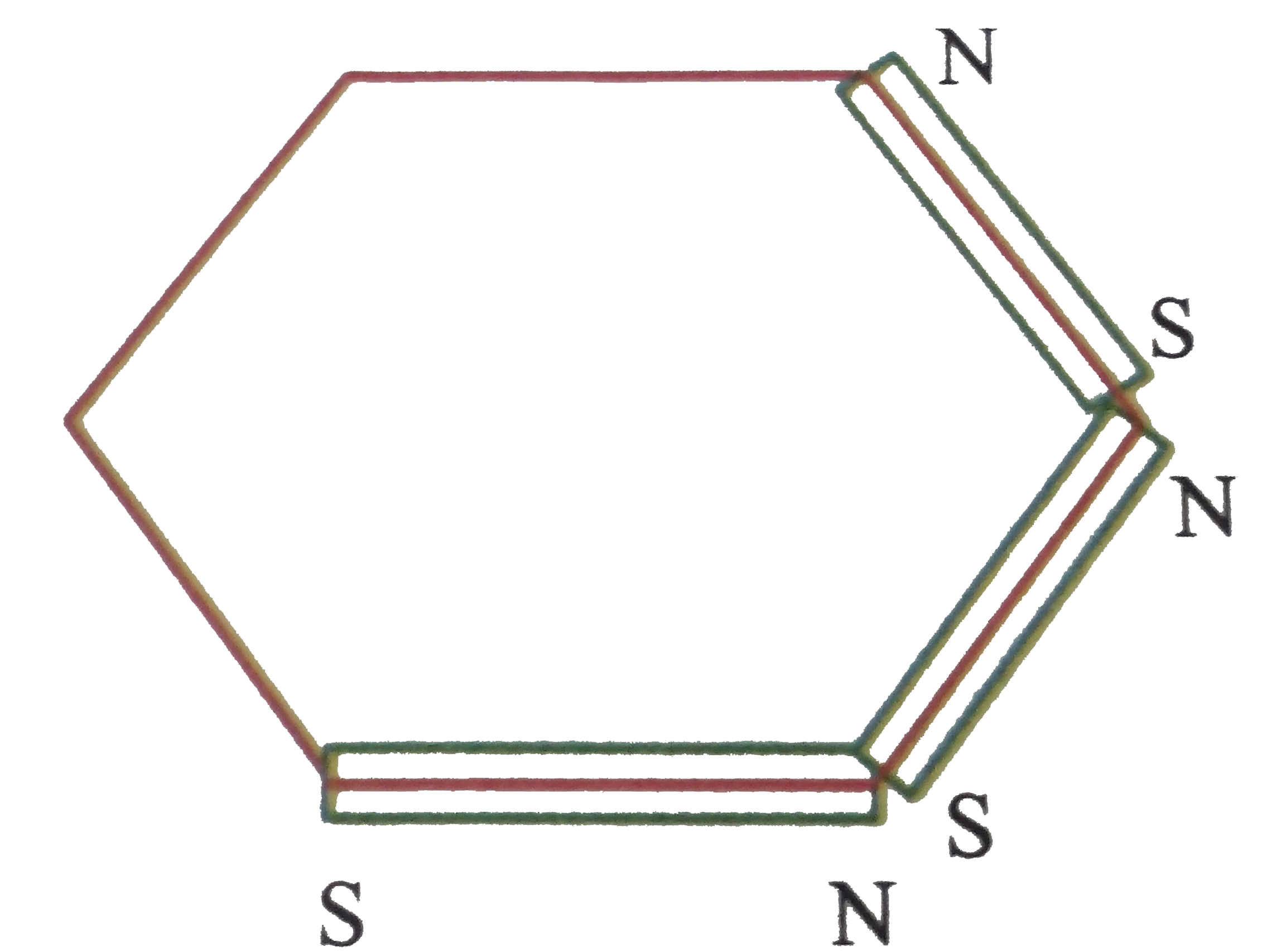
View SolutionThree identical thin bar magnets each of moment M are placed along three adjacent sides of a regular hexagon as shown in figure. The resultant magnetic moment of the system is
View SolutionThe mass, specific heat capacity and the temperature of a solid are 1000g,(1)/(2) cal/g - .^(@)C and 80^(@)C respectively. The mass of the liquid and the calorimeter are 900g and 200g . Initially,both are at room temperature 20^(@)C Both calorimeter and the solid are made of same material. In the steady state, temperature of mixture is 40^(@)C , then specific heat capacity of the unknown liquid.
View SolutionIn electrical calorimeter experiment, voltage across the heater is 100.0 V and current is 10.0 A . Heater is switched on for t = 700.0 s . Room temperature is theta_0 = 10.0^(@)C and final temperature of calorimeter and unknown liquid is theta_f = 73.0^(@) C . Mass of empty calorimeter is m_1 = 1.0kg and combined mass of calorimeter and unknown liquid is m_2 = 3.0 kg . Find the specificheat capacity of the unknown liquid in proper significant figures. Specific heat of calorimerter = 3.0xx10^3 j//kg .^(@) C .
View SolutionWater of mass m2=1kg is contained in a copper calorimeter of mass m1=1kg. Their common temperature t=10∘C. Now a piece of ice of mass m2=2kg and temperature is −11∘C dropped into the calorimeter. Neglecting any heat loss, the final temperature of system is. [specific heat of copper =0.1Kcal/kg∘C, specific heat of water =1Kcal/kg∘C, specific heat of ice =0.5Kcal/kg∘C, latent heat of fusion of ice =78.7Kcal/kg]
View SolutionFigure shows an electrical calorimeter to determine specific heat capacity of an unknown liquid, First of all, the mass of empty calorimeter (a copper container) is measured and suppose it is m1. Then the unknown liquid is poured in it. Now the combined mass of calorimeter+liquid system is measured and let it be m2. So the mass of liquid is (m2−m1). Initially both were at room temperature (θ0).
Now a heater is immeresed in if for time interval t. The voltage drop across the heater is V and current passing through it is I. Due to heat supplied, the temperature of both the liquid and calorimeter will rise simultaneously. After tsec, heater was switched off, and final temperature is θr. If there is no heat loss to surroundings. Heat supplied by the heater=Heat absorbed by the liquid+heat absorbed by the calorimeter (VI)t=(m2−m1)S1(θf−θ0)+m1Sc(θf−θ0)
The specific heat of the liquid S1=(VI)tθf−θ0−m1Sc(m2−m1)
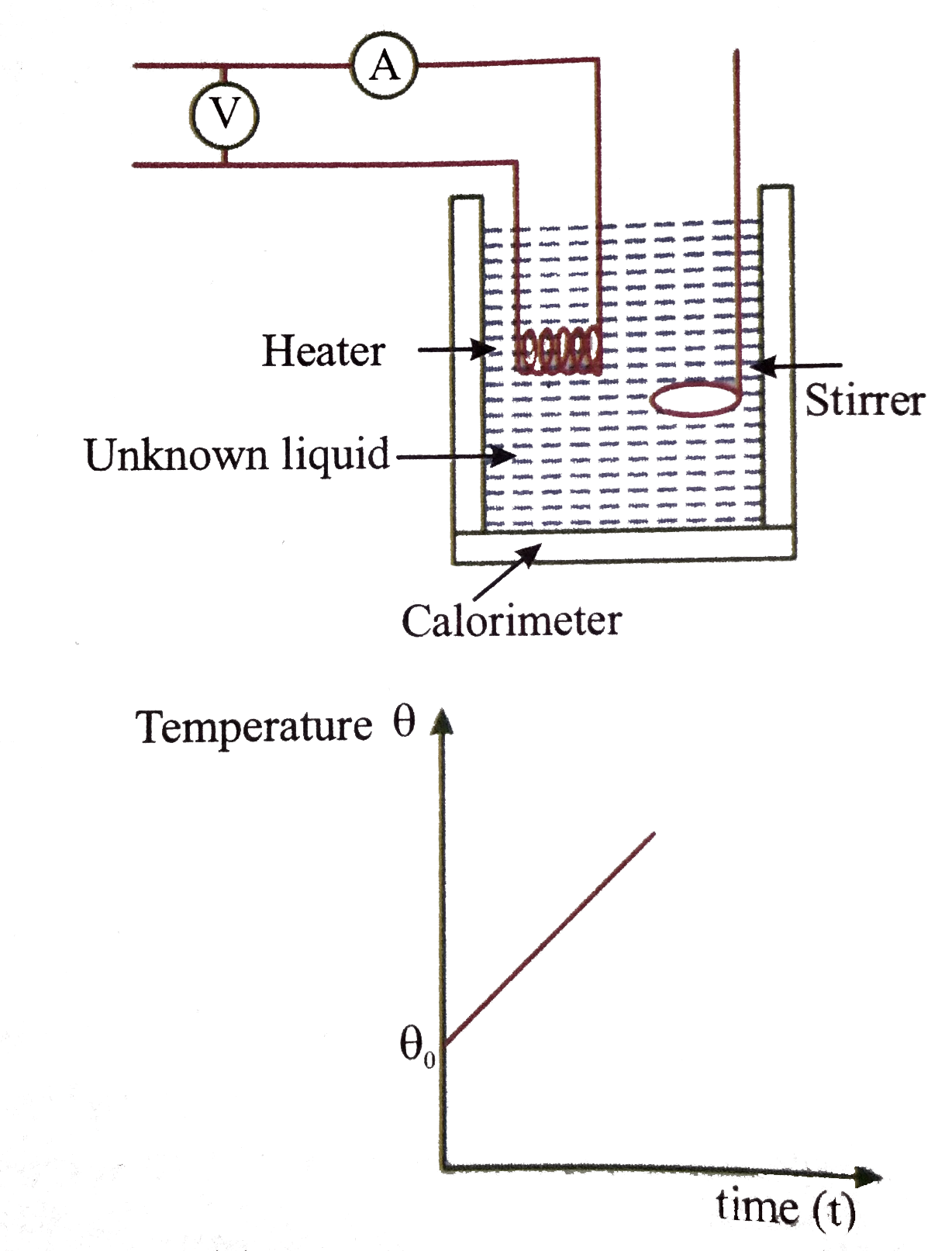
Radiation correction: There can be heat loss to environment. To compensate this loss, a correction is introduced.
Let the heater was on for tsec, and then it is switched off. Now the temperature of the mixture falls due to heat loss to environment. The temperature of the mixture is measured t/2sec. after switching off. Let the fall in temperature during this time is ɛ
Now the corrected final temperature is taken as θf=θf+ɛ
In this experiment voltage across the heater is 100.0V and current is 10.0A, and heater was switched on for t=700.0sec. Initially all elements were at room temperature θ∘=10.0∘C and final temperature was measured as θf=73.0∘C.
Mass of empty calorimeter ws 1.0kg and the combined mass of calorimeter + liquid is 3.0kg. The specific heat capacity of the calorimeter =3.0×103J/kg∘C. The falls in temperature 350 second after switching off the heater was 7.0∘C. Find the specific heat capacity of the unknown liquid in proper significant figures.
View SolutionFigure shows an electrical calorimeter to determine specific heat capacity of an unknown liquid, First of all, the mass of empty calorimeter (a copper container) is measured and suppose it is m_(1) . Then the unknown liquid is poured in it. Now the combined mass of calorimeter+liquid system is measured and let it be m_(2) . So the mass of liquid is (m_(2)-m_(1)) . Initially both were at room temperature ( theta_(0) ). Now a heater is immeresed in if for time interval t . The voltage drop across the heater is V and current passing through it is I . Due to heat supplied, the temperature of both the liquid and calorimeter will rise simultaneously. After t sec , heater was switched off, and final temperature is theta_(r) . If there is no heat loss to surroundings. Heat supplied by the heater=Heat absorbed by the liquid+heat absorbed by the calorimeter (VI)t=(m_(2)-m_(1))S_(1)(theta_(f)-theta_(0))+m_(1)S_(c)(theta_(f)-theta_(0)) The specific heat of the liquid S_(1)=(((VI)t)/(theta_(f)-theta_(0))-m_(1)S_(c))/((m_(2)-m_(1))) Radiation correction: There can be heat loss to environment. To compensate this loss, a correction is introduced. Let the heater was on for t sec , and then it is switched off. Now the temperature of the mixture falls due to heat loss to environment. The temperature of the mixture is measured t//2 sec . after switching off. Let the fall in temperature during this time is varepsilon Now the corrected final temperature is taken as theta_(f)=theta_(f)+varepsilon If the system were losing heat according to Newton's cooling law, the temperature of the mixture would change with time according to (while heater was on)
View SolutionTwo blocks of masses m_(1) and m_(2) are kept on a smooth horizontal table as shown in figure. Block of mass m_(1) (but not m_(2) is fastened to the spring. If now both the blocks are pushed to the left so that the spring is compressed a distance d. The amplitude of oscillatin of block of mass m_(1) after the system is released is
View SolutionMass of solid floating in liquid is m1 and mass of liquid is m2. Base area is A. Then pressure at bottom is p0+(m1+m2)gA
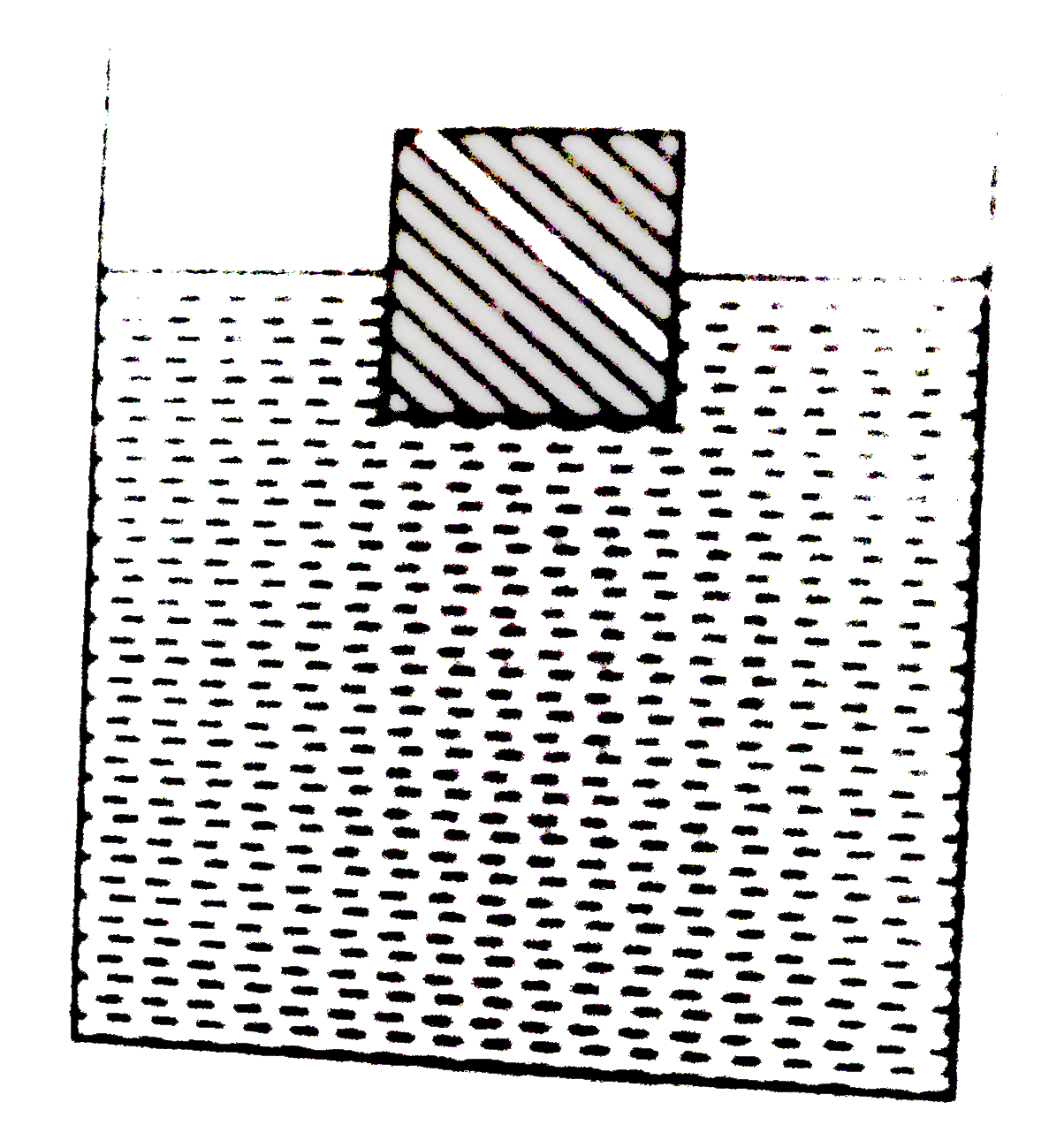
Reason : Upward force on liquid from base of vessel is pA, where p is pressure at bottom.
View SolutionTwo sphere of massM1 areM2 situated in air and the gravitational force between them is F. The space around the masses is now filled with liquid of specific gravity 3. The gravitational force will now be.........
View SolutionTwo liquids of masses M_(1) , and M_(2) and specific heats S_(1) , and S_(2) , respectively are mixed. The specific heat of the mixtureis
View SolutionThe mass, specific heat capacity and the temperature of a solid are 1000g,(1/2) ((cal)/g) and 80 degrees C respectively. The mass of the liquid and the calorimeter are 900g and 200g. Initially, both are at room temperature 20 degrees C. Both calorimeter and the solid are made of the same material. In the steady state, temperature of mixture is 40 degrees C, then specific heat capacity of the unknown liquid is;
View Solution
