ifA={(x,y):x2+y2=4,x,y∈R}and
B={(x,y):x2+y2=9,x,y∈R},then
A−B=ϕ
B−A=B
A∩B≠ϕ
A∩B=A
The correct Answer is:B
To solve the problem, we need to analyze the sets A and B defined in the question.
Step 1: Define the sets A and B
The set A is defined as:
A={(x,y):x2+y2=4,x,y∈R}
This represents a circle with a radius of 2 centered at the origin (0,0).
The set B is defined as:
B={(x,y):x2+y2=9,x,y∈R}
This represents a circle with a radius of 3 centered at the origin (0,0).
Step 2: Find A ∩ B (Intersection of A and B)
To find the intersection of sets A and B, we need to determine if there are any points (x, y) that satisfy both equations:
1. x2+y2=4 (from set A)
2. x2+y2=9 (from set B)
Since the left-hand sides of both equations cannot be equal (4 cannot equal 9), there are no points that satisfy both conditions. Therefore:
A∩B=∅
This means that the intersection of sets A and B is the empty set.
Step 3: Find A - B (Difference of A and B)
The difference A−B is defined as the set of elements that are in A but not in B. Since there are no common points between A and B, we have:
A−B=A
Thus, A−B is simply the set A itself.
Step 4: Find B - A (Difference of B and A)
Similarly, the difference B−A is defined as the set of elements that are in B but not in A. Again, since there are no common points between A and B, we have:
B−A=B
Thus, B−A is simply the set B itself.
Summary of Results
- A∩B=∅
- A−B=A
- B−A=B
The set A is defined as:
A={(x,y):x2+y2=4,x,y∈R}
This represents a circle with a radius of 2 centered at the origin (0,0).
B={(x,y):x2+y2=9,x,y∈R}
This represents a circle with a radius of 3 centered at the origin (0,0).
To find the intersection of sets A and B, we need to determine if there are any points (x, y) that satisfy both equations:
1. x2+y2=4 (from set A)
2. x2+y2=9 (from set B)
A∩B=∅
This means that the intersection of sets A and B is the empty set.
The difference A−B is defined as the set of elements that are in A but not in B. Since there are no common points between A and B, we have:
A−B=A
Thus, A−B is simply the set A itself.
Similarly, the difference B−A is defined as the set of elements that are in B but not in A. Again, since there are no common points between A and B, we have:
B−A=B
Thus, B−A is simply the set B itself.
- A∩B=∅
- A−B=A
- B−A=B
Topper's Solved these Questions
- SETSBOOK - OBJECTIVE RD SHARMACHAPTER - SETSEXERCISE - Chapter Test
30 Videos
- SETSBOOK - OBJECTIVE RD SHARMACHAPTER - SETSEXERCISE - Section I - Solved Mcqs
24 Videos
- SEQUENCES AND SERIESBOOK - OBJECTIVE RD SHARMACHAPTER - SEQUENCES AND SERIESEXERCISE - Chapter Test
60 Videos
- STRAIGHT LINESBOOK - OBJECTIVE RD SHARMACHAPTER - STRAIGHT LINESEXERCISE - Chapter Test
34 Videos
Similar Questions
In some question of sets, we have to make the use of graphs
For example
A={(x,y):y=ex,x∈R}
B={{x,y}:y=−x.x∈R}
Find n(A∩B)
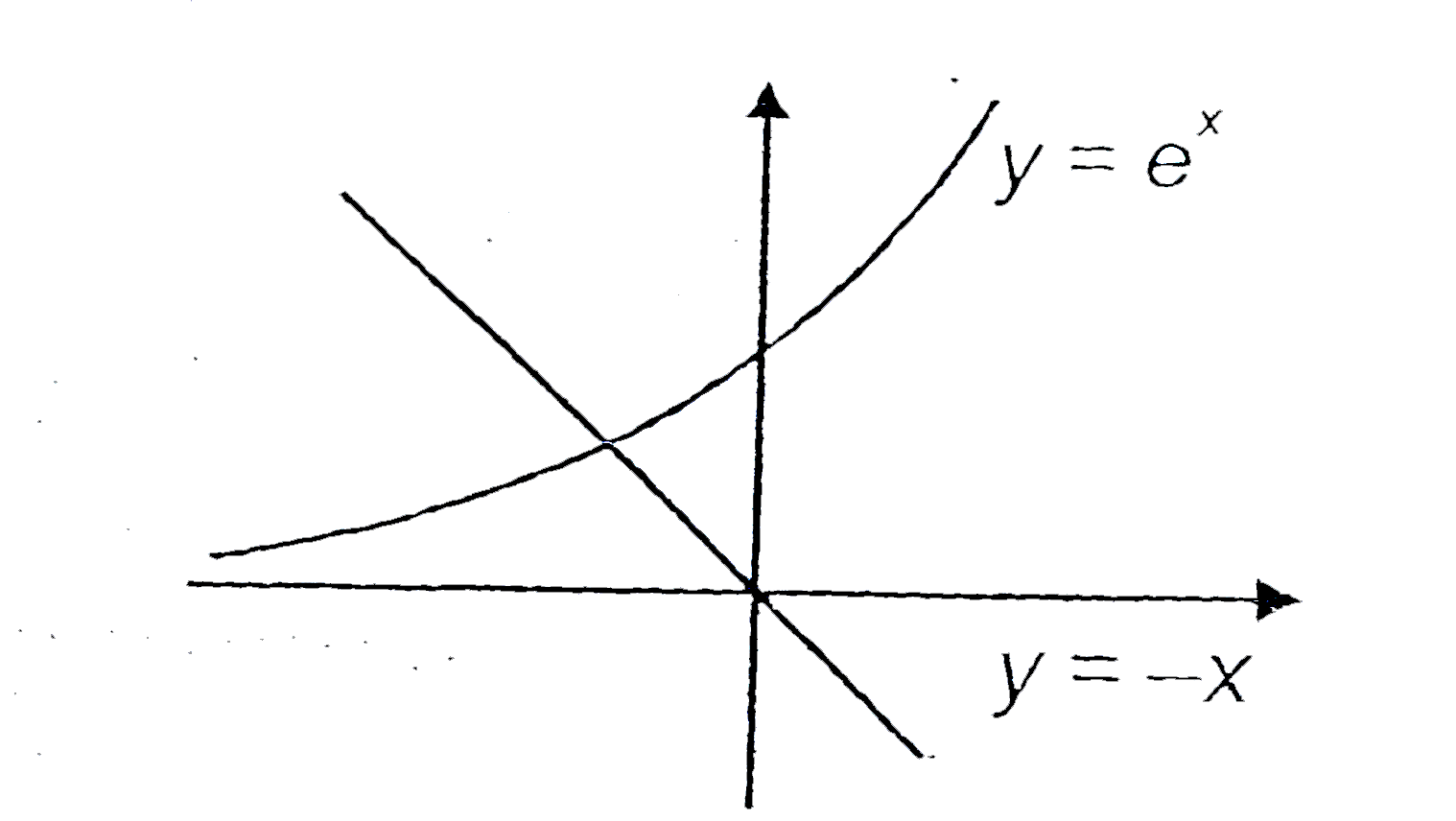
It is clear that y=exandy=−x intersect at one pont. Hence n(A∩B)=1
A={(x,y):x2+y2≤2,x,y∈R}
B={{x,y):y≥x2,x,y∈R}
Then domain of A∩B is
View SolutionIf A={(x,y):y=ex,x∈R} and B={(x,y):y=e−2x,x∈R}, then
View Solution
Knowledge Check
ifA={(x,y):x2+y2=4,x,y∈R}and
B={(x,y):Y=|x|,x,y∈R} thenAA∩B=ϕBA∩B is singlcton setCA∩B contains two elements onlyDA∩B contains three elements only .ifA={(x,y):x2+y2≤1,x,y∈R]and
B={(x,y):x2+y2≤x2+y2≤4,x,y∈R]thenAA−B=ABB−A=BCA−B=ϕDB−A=ϕIf A={(x,y):x2+y2≤1:x,y∈R} and B={(x,y):x2+y2≥4,x,y∈R}, then
AA−B=ϕBB−A=ϕCA∩B≠ϕDA∩B=ϕ
If A={(x,y):x2+y2≤1:x,y∈R} and B={(x,y):x2+y2≥4,x,y∈R}, then
View SolutionLet A={(x,y):x2+y2=36} and B={(x,y):x2+9y2=100}, Then
View SolutionifA={(x,y):y=4x,x≠0}and
B={(x,y):x2+y2=8,x,y∈R},then
View SolutionIfA={x,y):x2+y2=25}and
B={(x,y):x2+9y2=144}, then A∩B contains
View SolutionLet A={(x,y)∣y=x,x∈R}andB={(x,y)∣y=−x,x∈R} then
View Solution
