Measurements show that the cell potential is affected by a number of factors such as
(i) the nature of the substance that makes up each half-cell
(ii) the concentration of dissolved ions and molecules
(iii) the pressures of gases
(iv) the terpreature
(i), (ii), (iii), (iv)
(ii), (iv)
(i), (ii)
(ii), (iii), (iv)
The correct Answer is:A
These are the same factors that determine both the Gibbs energy difference between substances and the value of the equilibrium constant, , for a chemical systeam.
Topper's Solved these Questions
- BOOK - R SHARMACHAPTER - ELECTROCHEMISTRYEXERCISE - Follow-up Test 513videos
ELECTROCHEMISTRY
- BOOK - R SHARMACHAPTER - ELECTROCHEMISTRYEXERCISE - Follow-up Test 612videos
ELECTROCHEMISTRY
- BOOK - R SHARMACHAPTER - ELECTROCHEMISTRYEXERCISE - Follow-up Test 37videos
ELECTROCHEMISTRY
- BOOK - R SHARMACHAPTER - COORDINATION COMPOUNDSEXERCISE - Archives56videos
COORDINATION COMPOUNDS
- BOOK - R SHARMACHAPTER - GENERAL PRINCIPALS AND ISOLATION OF ELEMENTSEXERCISE - Arechives16videos
GENERAL PRINCIPALS AND ISOLATION OF ELEMENTS
Similar Questions
Two bulbs A and B of equal capacity are filled with He and SO2, respectively, at the same temperature.
(a) If the pressures in the two bulbs are same, what will be the ratio of the velocities of the molecules of the two gases?
(b)At what temperature will the velocity of SO2 molecules become half of the velocity of He molecules at 27∘C?
(c) How will the velocities be affected if the volume of B becomes four times that of A?
(d) How will the velocities be affected if half of the molecules of SO2 are removed from B?View SolutionStatement-I: In the Daniel cell, if concentration of Cu2+ and Zn2+ ions are doubled the emf of the cell will not change.
Because Statement-II: If the concentration of ions in contact with the metals is doubled, the electrode potential is doubled.View Solution
Knowledge Check
- Question 1 - Select One
Which of the following factor (s) affect the solubility of a gaseous solution in the fixed volume of liquid solvent?
(i) Nature of solute
(ii) Temperatute
(iii) PressureA(i) and (iii) at constant TB(i) and (ii) at constant PC(ii) and (iii) onlyD(iii) only. - Question 2 - Select One
Which of the following factor (s) affect the solubility of a gaseous solute in the fixed volume of liquid solvent?
(i) nature of solute
(ii) temperature
(iii) pressureAAll of theseB(i) onlyC(ii) and (iii) onlyD(iii) only - Question 3 - Select One
Solubility of a substance is its maximum amount that can be dissovled in a specified amount of solvent. It depends upon
(i) nature of solute
(ii) nature of solvent
(iii) temperature
(iv) pressureA(i) , (ii) and (iii)B(i), (iii) and (iv)C(i) and (iv)D(i), (ii), (iii) and (iv)
In the kinetic theory of gases, which of these statements is/are true ?
(i) The pressure of a gas is proportional to the mean speed of the molecules. (ii) The root mean square speed of the molecules is proportional to the pressure. (iii) The rate of diffusion is proportional to the mean speed of the molecules. (iv) The mean translational kinetic energy of a gas is proportional to its kelvin temperature.View SolutionSolubility of a substance is its maximum amount that can be dissolved in a specified amount of solvent. It depends upon
(i)nature of solute , (ii)nature of solvent , (iii)temperature , (iv)pressureView SolutionTitration are one of the methods we can use to discover the precise concentration of solutions. A typical titration involves adding a solution from a burette to another solution in a flask. The end point of the titration is found by watching a colour change taking place.However, a problem arises when a suitable indicator cannot be found, or when the colour change involved are unclear. In these cases, redox potential may sometimes come to the rescue.
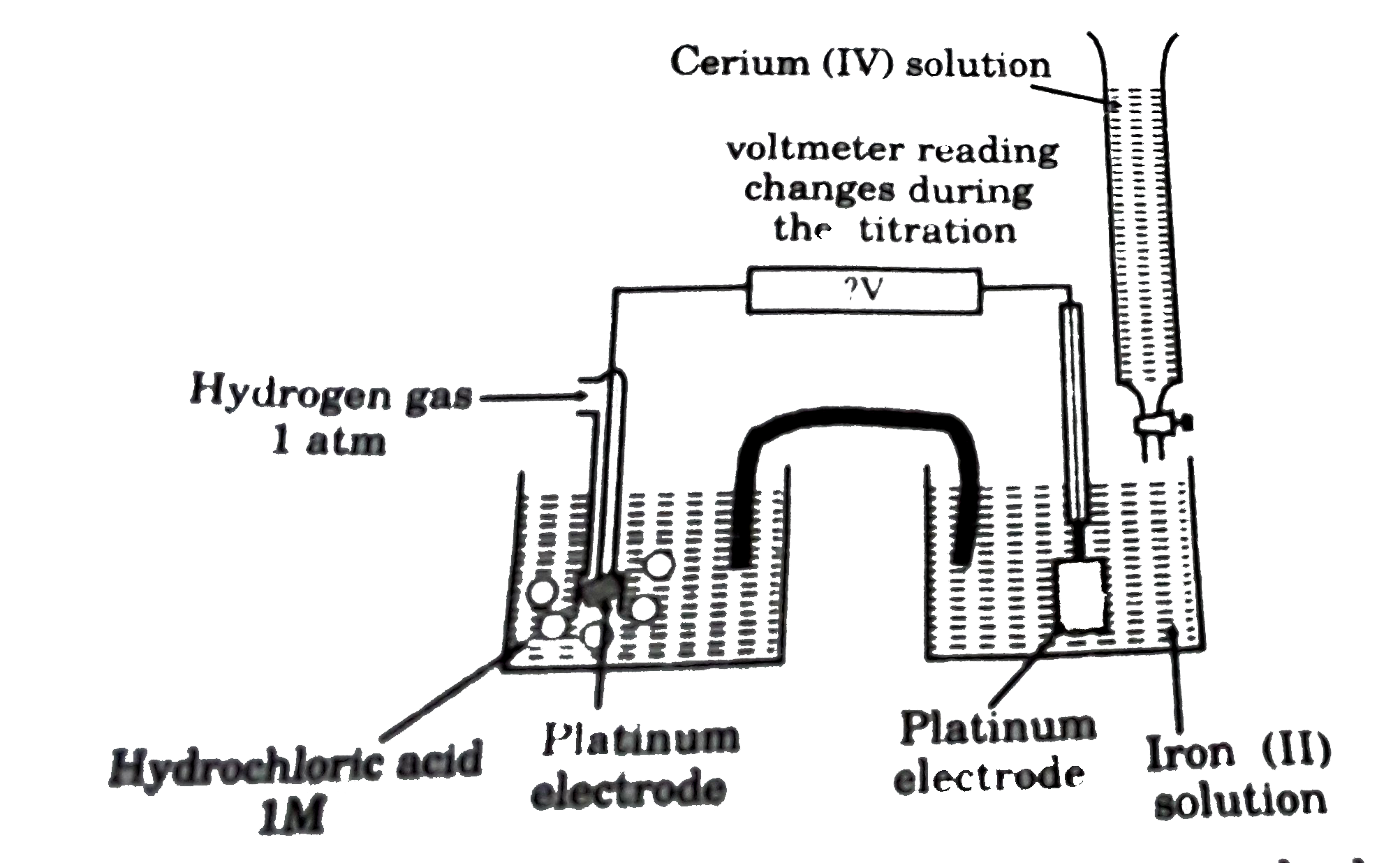
A perticularly well known example (Fig.) is a method of discovering then concentration of iron (II) ions in a solution by titrating them with a solution of cerium (IV). The redox potential that are of interest here areE∘Fe3+∣Fe2+=0.77VandE∘Ce4+∣Ce3+=1.61V. These tell us that cerium (IV) ions are the oxidising agents. They should react according to the equation
Fe2+(aq)+Ce4+(aq)→Fe3+(aq)+Ce3+(aq).
Now imagine that we know the concentration of the cerium (IV) ions solution in the burette. We want to measure the concentration of the cerium (IV) solution from the burette, some of the iron (II) ions are will be oxidised. As a consequence the beaker would now contain large number of unreacted iron (II) ions , but also some iron (III) ions as well. All of the cerium (III). The solution in the beaker now represents an iron (III)/iron(II) half cell although not at standard conditions.Thus , the emf of the cell will be near, but not equal to E∘Fe3+∣Fe2+.
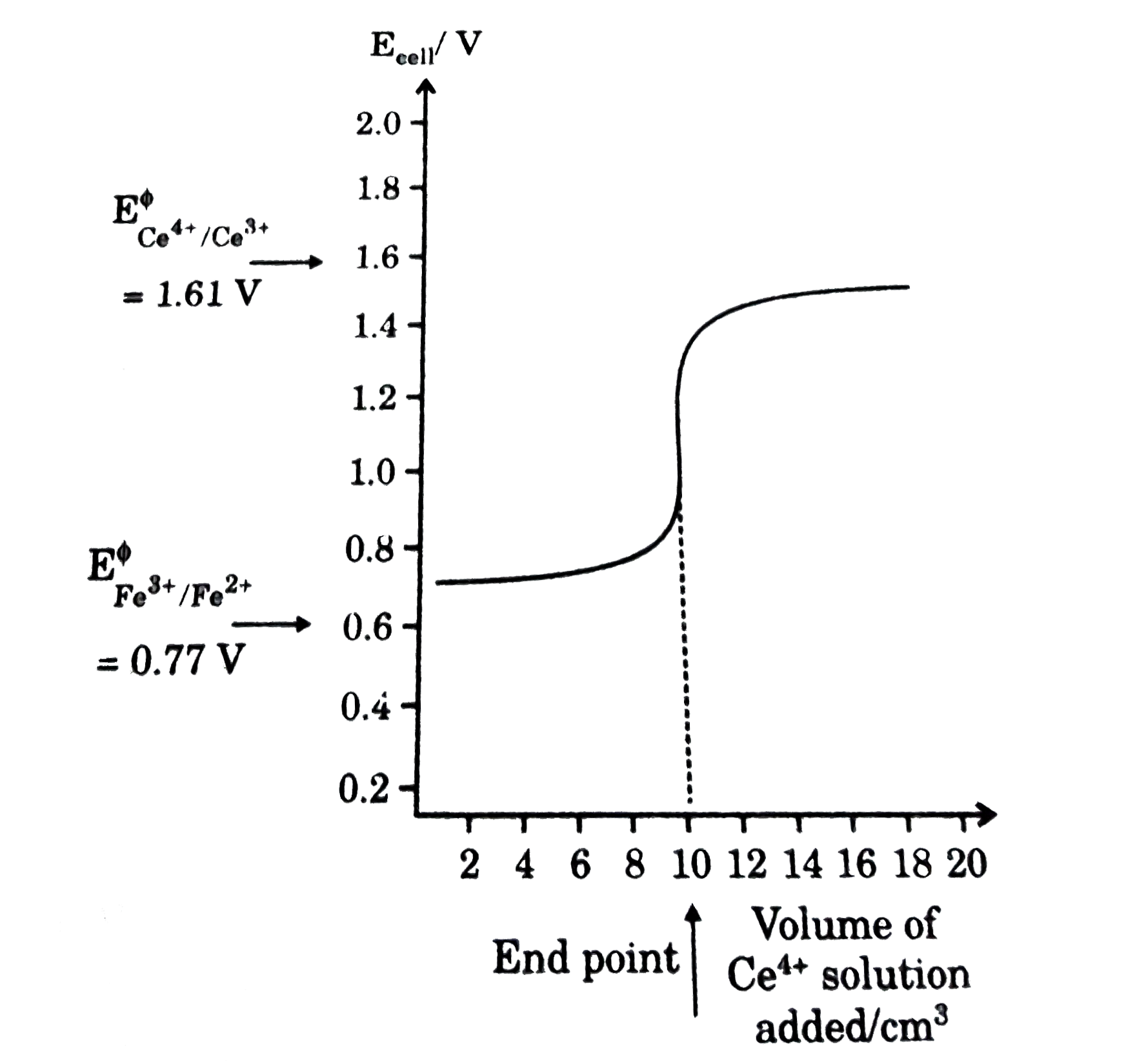
If we continue to add cerium (IV) solution , the number of iron (II) ions is gradually reduced and eventually only a very few are left (Table).At this stage the next few drops of cerium (IV) solution convert all the remaining irom (II) ions into iron (III), and some of the cerium (IV) ions are left unreacted. Once this happens we no longer have an iron (III)/iron(II) half-cell. Instead we have a solution in which there is a large number of cerium (III) ions and a smaller number of cerium (IV) ions. The solution in the beaker now behaves as a cerium (IV)/cerium(III)half-cell (although not a standard one.)
Just before all the iron (II) ions are converted into iron (III) we have a cell with an EMF of around +0.77V. After all the iron (II) ions are oxidised we have a cell with an emf of about +1.61V. This rapid rise in emf occurs with the addition of just one drop of cerium (IV) solution. You should be able to understand why a graph of cell emf against volume of cerium (IV) solution of the iron (II) solution calculated in the usual way.
When an ion is converted into a complex ion, the redox potential change. you can see this in the combination of standard emf of the iron (III)/iron(II) system (+0.36V). The cyanide ion is said to stabilize the oxidation state of the iron. If you were to make up a cell
Pt(s)∣∣ ∣∣Fe(CN)3−61mol dm−1(aq),Fe(CN)4−6∣∣ ∣∣∣∣ ∣∣Fe3+(aq)1mol dm−3,Fe2+(aq)∣∣ ∣∣Pt(s)
what would be the emf and what would be the cell reaction?
View SolutionTitration are one of the methods we can use to discover the precise concentration of solutions. A typical titration involves adding a solution from a burette to another solution in a flask. The end point of the titration is found by watching a colour change taking place.However, a problem arises when a suitable indicator cannot be found, or when the colour change involved are unclear. In these cases, redox potential may sometimes come to the rescue.
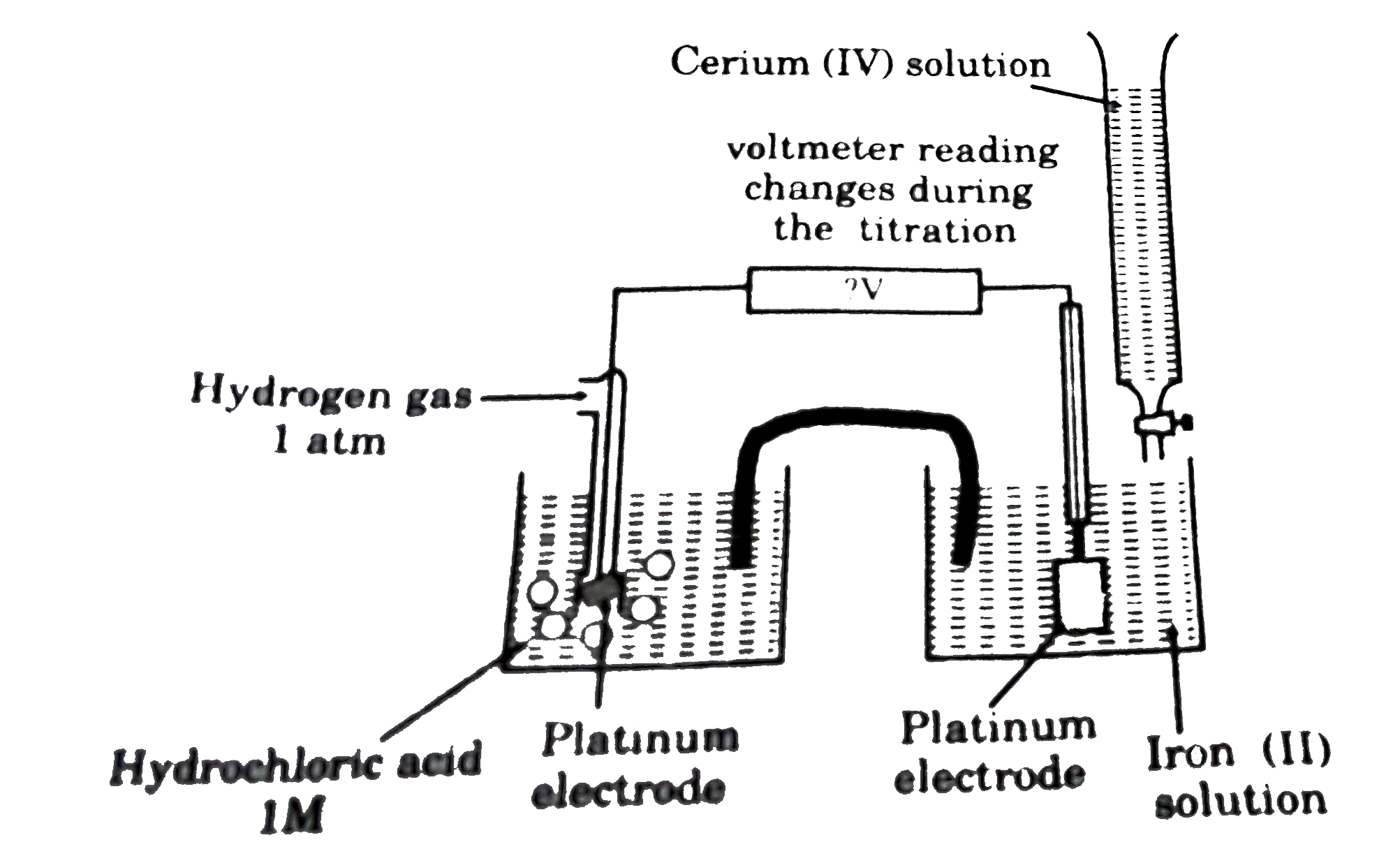
A perticularly well known example (Fig.) is a method of discovering then concentration of iron (II) ions in a solution by titrating them with a solution of cerium (IV). The redox potential that are of interest here areE∘Fe3+∣Fe2+=0.77VandE∘Ce4+∣Ce3+=1.61V. These tell us that cerium (IV) ions are the oxidising agents. They should react according to the equation
Fe2+(aq)+Ce4+(aq)→Fe3+(aq)+Ce3+(aq).
Now imagine that we know the concentration of the cerium (IV) ions solution in the burette. We want to measure the concentration of the cerium (IV) solution from the burette, some of the iron (II) ions are will be oxidised. As a consequence the beaker would now contain large number of unreacted iron (II) ions , but also some iron (III) ions as well. All of the cerium (III). The solution in the beaker now represents an iron (III)/iron(II) half cell although not at standard conditions.Thus , the emf of the cell will be near, but not equal to E∘Fe3+∣Fe2+.
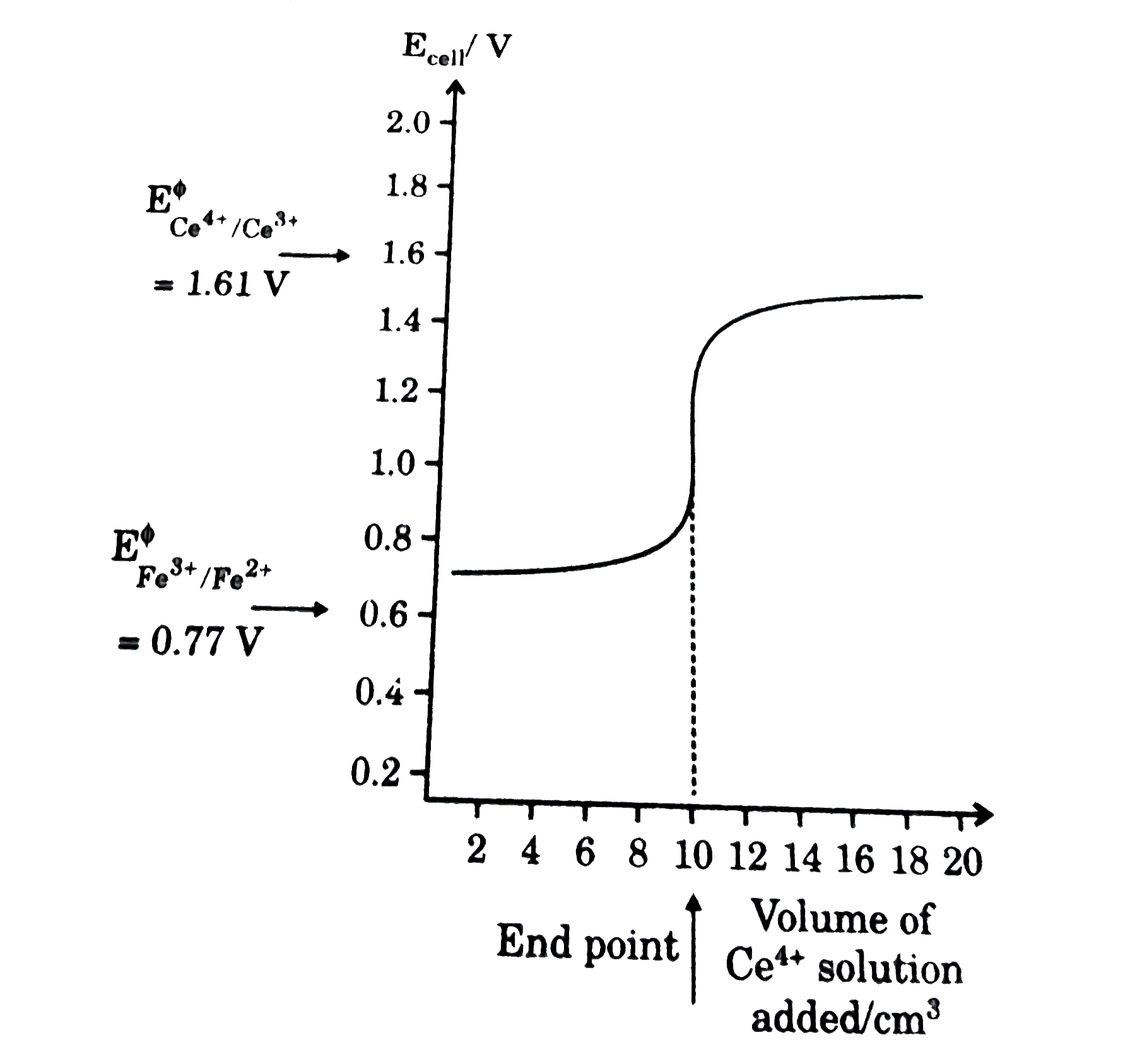
If we continue to add cerium (IV) solution , the number of iron (II) ions is gradually reduced and eventually only a very few are left (Table).At this stage the next few drops of cerium (IV) solution convert all the remaining irom (II) ions into iron (III), and some of the cerium (IV) ions are left unreacted. Once this happens we no longer have an iron (III)/iron(II) half-cell. Instead we have a solution in which there is a large number of cerium (III) ions and a smaller number of cerium (IV) ions. The solution in the beaker now behaves as a cerium (IV)/cerium(III)half-cell (although not a standard one.)
Just before all the iron (II) ions are converted into iron (III) we have a cell with an EMF of around +0.77V. After all the iron (II) ions are oxidised we have a cell with an emf of about +1.61V. This rapid rise in emf occurs with the addition of just one drop of cerium (IV) solution. You should be able to understand why a graph of cell emf against volume of cerium (IV) solution of the iron (II) solution calculated in the usual way.
The cell shown below was set up
Pt∣∣ ∣∣Fe3+(aq),Fe2+(aq)1mol dm−3,∣∣ ∣∣∣∣ ∣∣Br−(aq)∣Br2(l)1mol dm−3,∣∣ ∣∣Pt(s)
what would be the cell emf? If potassium cyanide solution were added to the left hand half cell (with due care!) what would you expect to happen to the emf of the cell ? E∘Br2/Br−=1.07V and use data of previous question, if required.View SolutionTitration are one of the methods we can use to discover the precise concentration of solutions. A typical titration involves adding a solution from a burette to another solution in a flask. The end point of the titration is found by watching a colour change taking place.However, a problem arises when a suitable indicator cannot be found, or when the colour change involved are unclear. In these cases, redox potential may sometimes come to the rescue.
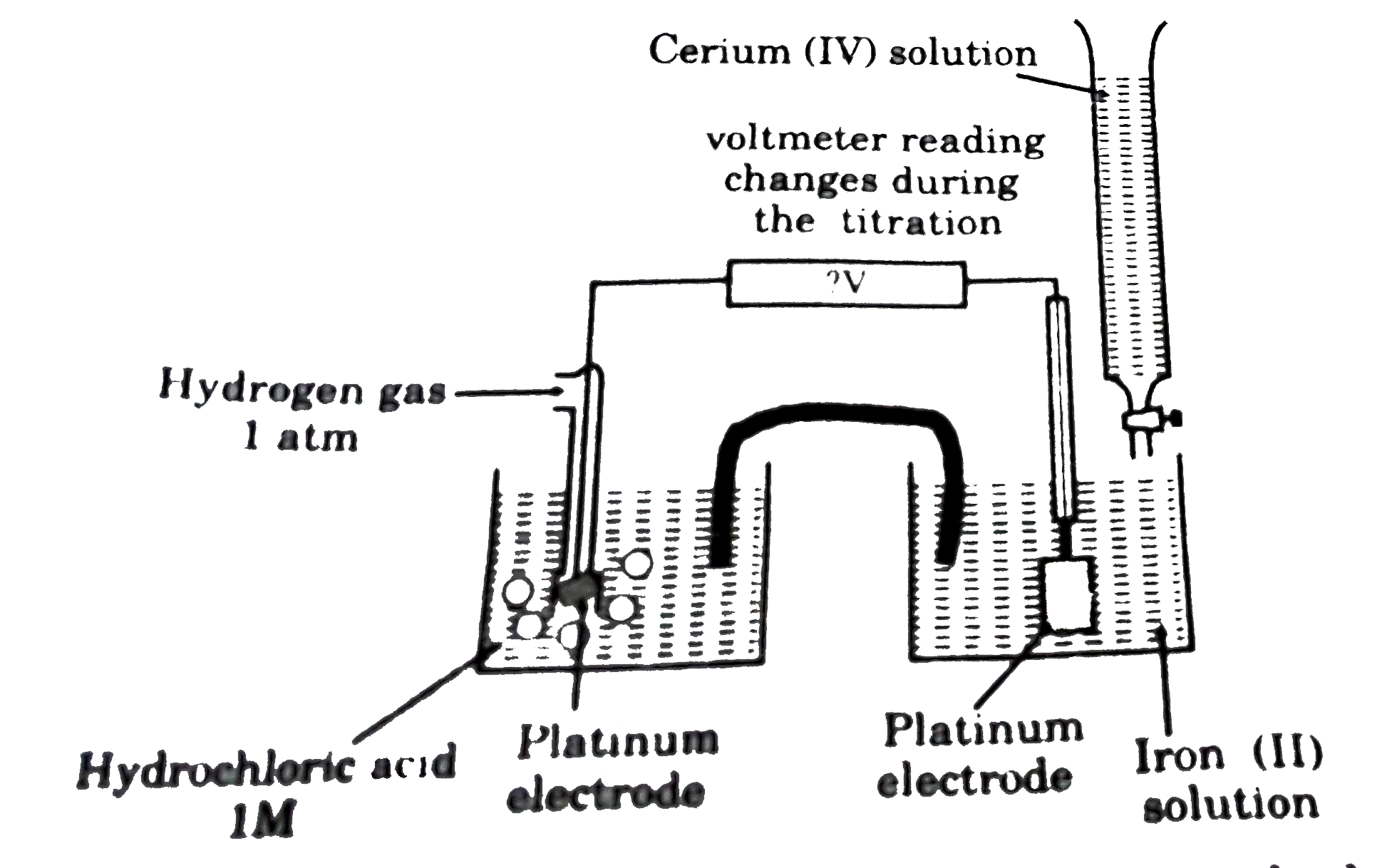
A perticularly well known example (Fig.) is a method of discovering then concentration of iron (II) ions in a solution by titrating them with a solution of cerium (IV). The redox potential that are of interest here areE∘Fe3+∣Fe2+=0.77VandE∘Ce4+∣Ce3+=1.61V. These tell us that cerium (IV) ions are the oxidising agents. They should react according to the equation
Fe2+(aq)+Ce4+(aq)→Fe3+(aq)+Ce3+(aq).
Now imagine that we know the concentration of the cerium (IV) ions solution in the burette. We want to measure the concentration of the cerium (IV) solution from the burette, some of the iron (II) ions are will be oxidised. As a consequence the beaker would now contain large number of unreacted iron (II) ions , but also some iron (III) ions as well. All of the cerium (III). The solution in the beaker now represents an iron (III)/iron(II) half cell although not at standard conditions.Thus , the emf of the cell will be near, but not equal to E∘Fe3+∣Fe2+.
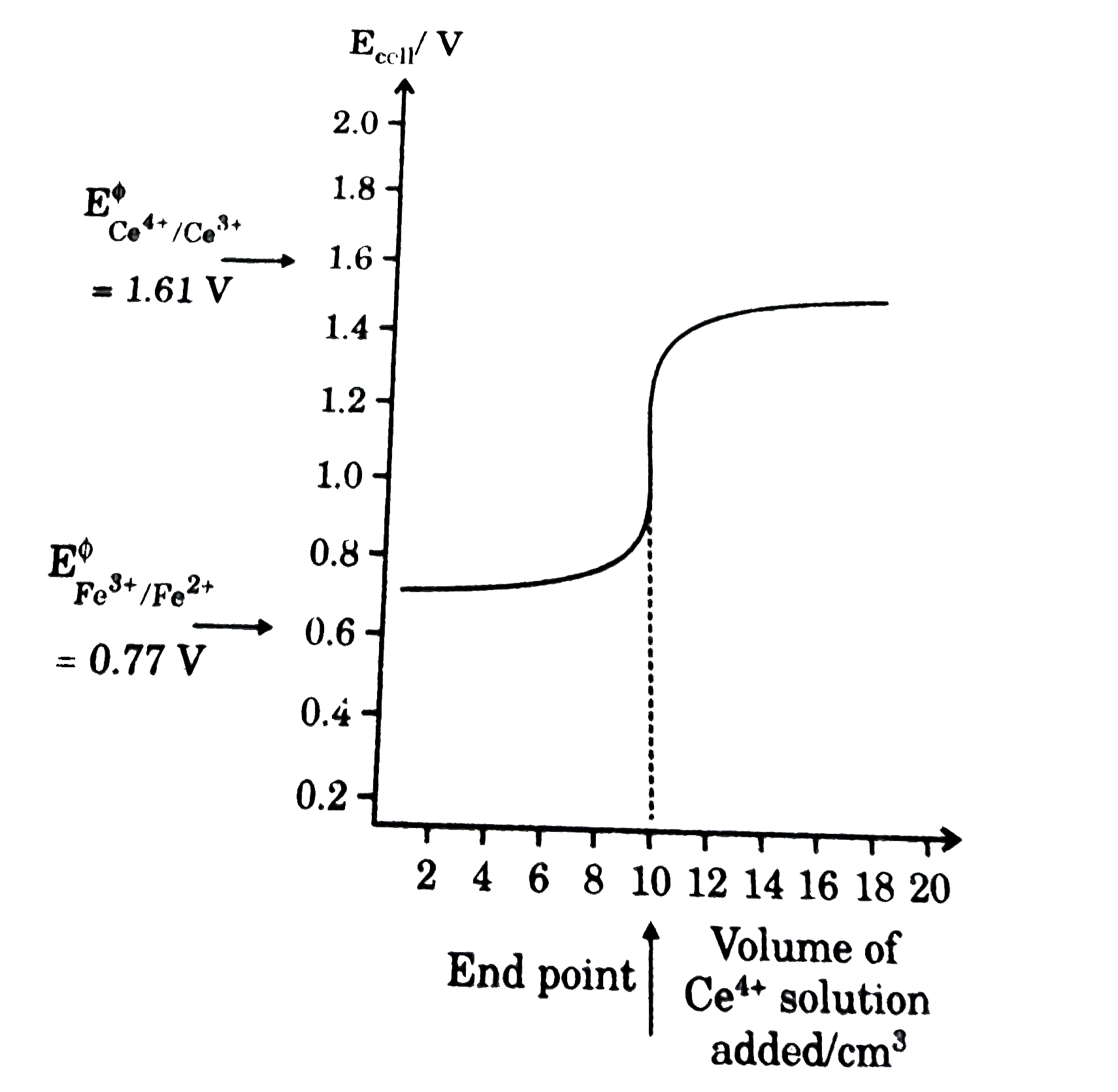
If we continue to add cerium (IV) solution , the number of iron (II) ions is gradually reduced and eventually only a very few are left (Table).At this stage the next few drops of cerium (IV) solution convert all the remaining irom (II) ions into iron (III), and some of the cerium (IV) ions are left unreacted. Once this happens we no longer have an iron (III)/iron(II) half-cell. Instead we have a solution in which there is a large number of cerium (III) ions and a smaller number of cerium (IV) ions. The solution in the beaker now behaves as a cerium (IV)/cerium(III)half-cell (although not a standard one.)
Just before all the iron (II) ions are converted into iron (III) we have a cell with an EMF of around +0.77V. After all the iron (II) ions are oxidised we have a cell with an emf of about +1.61V. This rapid rise in emf occurs with the addition of just one drop of cerium (IV) solution. You should be able to understand why a graph of cell emf against volume of cerium (IV) solution of the iron (II) solution calculated in the usual way.
Imagine you were given a solution of potassium dichromate (VI) in a beaker and a solution of iron (II) sulphate in a burette. You do not know the concentration of dichromate (VI) ions , but the concentration of the iron (II) solution is known. Your task it to carry out a redox titration using the two solutions in order to determine the concentration of dichromate (VI) ions. Sketch a graph showing how the emf changes in the course of the above titration.
ECr2O2−7/Cr3+=1.33V,EFe3+/Fe2+=0.77VView Solution

