A ball is thrown with speed at an angle with horizontally from the top of a tower of height . Choose the correct option
the vertical component of velocity first decreases to zero and then increases
the ball reaches the ground after
if the ball strikes the ground at maximum horizontal distance from the tower for this the angle of projection should be less than
all option are correct
The correct Answer is:D
To solve the problem step by step, we need to analyze the motion of the ball thrown from the tower. Here’s how we can approach it:
Step 1: Identify the initial parameters
- Initial speed of the ball, u=40m/s
- Angle of projection, θ=30∘
- Height of the tower, h=60m
Step 2: Break down the initial velocity into components
The initial velocity can be resolved into horizontal and vertical components:
- ux=ucosθ=40cos30∘=40×√32=20√3m/s
- uy=usinθ=40sin30∘=40×12=20m/s
Step 3: Use the vertical motion equation to find the time of flight
The vertical motion can be described by the equation:
y=uyt−12gt2
where y is the vertical displacement (which will be -60 m since it falls down), g=10m/s2 (acceleration due to gravity), and t is the time of flight.
Substituting the values:
−60=20t−12⋅10⋅t2
This simplifies to:
−60=20t−5t2
Rearranging gives:
5t2−20t−60=0
Dividing through by 5:
t2−4t−12=0
Step 4: Solve the quadratic equation
Using the quadratic formula t=−b±√b2−4ac2a:
Here, a=1,b=−4,c=−12:
t=−(−4)±√(−4)2−4⋅1⋅(−12)2⋅1
t=4±√16+482
t=4±√642
t=4±82
This gives us two possible solutions:
t=122=6andt=−42=−2(not valid)
Thus, t=6s.
Step 5: Verify the options
1. Vertical component of velocity first decreases to zero then increases: This is true because the ball goes up first, slows down, stops, and then falls down.
2. The ball reaches the ground after 6 seconds: This is confirmed as we calculated t=6s.
3. If the ball strikes the ground at maximum horizontal distance from the tower, the angle of projection should be less than 45 degrees: This is also true since for maximum range, the angle should be less than 45 degrees when launched from a height.
Conclusion
All options provided in the question are correct.
---
- Initial speed of the ball, u=40m/s
- Angle of projection, θ=30∘
- Height of the tower, h=60m
The initial velocity can be resolved into horizontal and vertical components:
- ux=ucosθ=40cos30∘=40×√32=20√3m/s
- uy=usinθ=40sin30∘=40×12=20m/s
The vertical motion can be described by the equation:
y=uyt−12gt2
where y is the vertical displacement (which will be -60 m since it falls down), g=10m/s2 (acceleration due to gravity), and t is the time of flight.
−60=20t−12⋅10⋅t2
This simplifies to:
−60=20t−5t2
Rearranging gives:
5t2−20t−60=0
Dividing through by 5:
t2−4t−12=0
Using the quadratic formula t=−b±√b2−4ac2a:
Here, a=1,b=−4,c=−12:
t=−(−4)±√(−4)2−4⋅1⋅(−12)2⋅1
t=4±√16+482
t=4±√642
t=4±82
This gives us two possible solutions:
t=122=6andt=−42=−2(not valid)
Thus, t=6s.
1. Vertical component of velocity first decreases to zero then increases: This is true because the ball goes up first, slows down, stops, and then falls down.
2. The ball reaches the ground after 6 seconds: This is confirmed as we calculated t=6s.
3. If the ball strikes the ground at maximum horizontal distance from the tower, the angle of projection should be less than 45 degrees: This is also true since for maximum range, the angle should be less than 45 degrees when launched from a height.
All options provided in the question are correct.
Topper's Solved these Questions
Similar Questions
A ball is thrown with velocity 40m/s at angle 30∘ with horizontal from the top of a tower of height 60m. At what horizontal distance from the foot of tower, the ball will strike the gorund ?
View SolutionA ball is thrown at a speed of 40 m/s at an angle of 600 with the horizontal. Find a. the maximum height reached and b. the range of te ball. Take g=10ms2.
View Solution
Knowledge Check
- Question 1 - Select One
Figure shows a projectile thrown with speed u = 20 m/s at an angle 30∘ with horizontal from the top of a building 40 m high. Then the horizontal range of projectile is
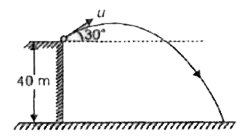 A20√3 mB40√3 mC40 mD20 m
A20√3 mB40√3 mC40 mD20 m - Question 2 - Select One
A ball is projected at an angle of 30∘ above with the horizontal from the top of a tower and strikes the ground in 5s at an angle of 45∘ with the horizontal. Find the height of the tower and the speed with which it was projected.
A50(√3−1)ms−1B50(√2−1)ms−1C70(√3−1)ms−1D80(√3−1)ms−1 - Question 3 - Select One
A ball is thrown horizontally with a speed of 20m/s from the top of a tower of height 100m
Time taken by the ball to strike the ground isA√20sB2√20sC4√20sD10s
A ball is projected at an angle of 30∘ above with the horizontal from the top of a tower ans strikes the ground in 5sec at angle of 45∘ with the horizontal. Find the hieght of the lower and the speede with which it was projected.
View SolutionA ball is thrown horizontally with a speed of 20m/s from the top of a tower of height 100m
Horizontal distance travelled by the before it strickes the ground isView SolutionA ball of mass m is thrown at an angle of 45∘ to the horizontal,, from the top of a 65m high tower AB as shown in Fig. at t=0. Another identical ball is thrown with velocity 20m/s horizontally towards AB from the top of a 30m high tower CD1s after the projection of the first ball. Both the balls move the same vertical plane. If they collide in mid-air,

the height from the ground where the two balls will collide isView SolutionA ball of mass m is thrown at an angle of 45∘ to the horizontal,, from the top of a 65m high tower AB as shown in Fig. at t=0. Another identical ball is thrown with velocity 20m/s horizontally towards AB from the top of a 30m high tower CD1s after the projection of the first ball. Both the balls move the same vertical plane. If they collide in mid-air,

. the velocity of combined ball just after they struck together isView SolutionA ball of mass m is thrown at an angle of 45∘ to the horizontal,, from the top of a 65m high tower AB as shown in Fig. at t=0. Another identical ball is thrown with velocity 20m/s horizontally towards AB from the top of a 30m high tower CD1s after the projection of the first ball. Both the balls move the same vertical plane. If they collide in mid-air,

the two balls will collide at time t=View Solution

