
A ball is attached to a string of length L and the ball is given velocity v0 at its lowest point. Find the speed of the ball at point B,C and D. Assume that the ball is moving in vertical circle.
Here forces acting on the ball are gravitational force and tension in the string. Gravitational force is conservative and work done by tension is zero, because it is always perpendicular to displacement. Hence, conservation of mechanical energy is applicable.
Assuming a horizontal line through A as the reference line,
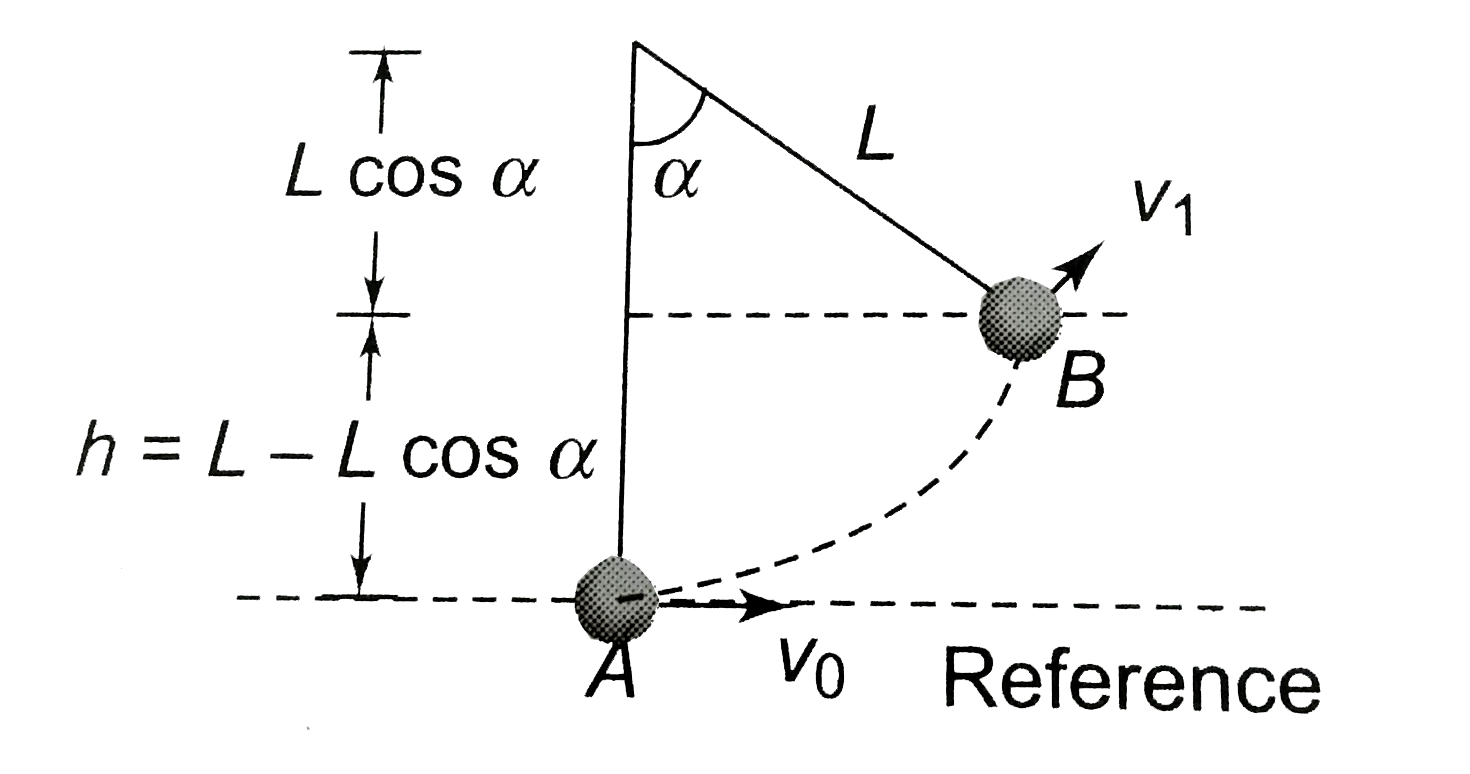
KA=12mv20,UA=0
KB=12mv21,UB=mg=mgL(1−cosα)
KA+UA=KB+UB
12mv20+0=12mv21+mgL(1−cosα)
v1=√v20−2gL(1−cosα)

KC=12mv22,UC=mg(L+Lcosβ)
KA+UA=KC+UC
v2=√v20−2gL(1+cosβ)
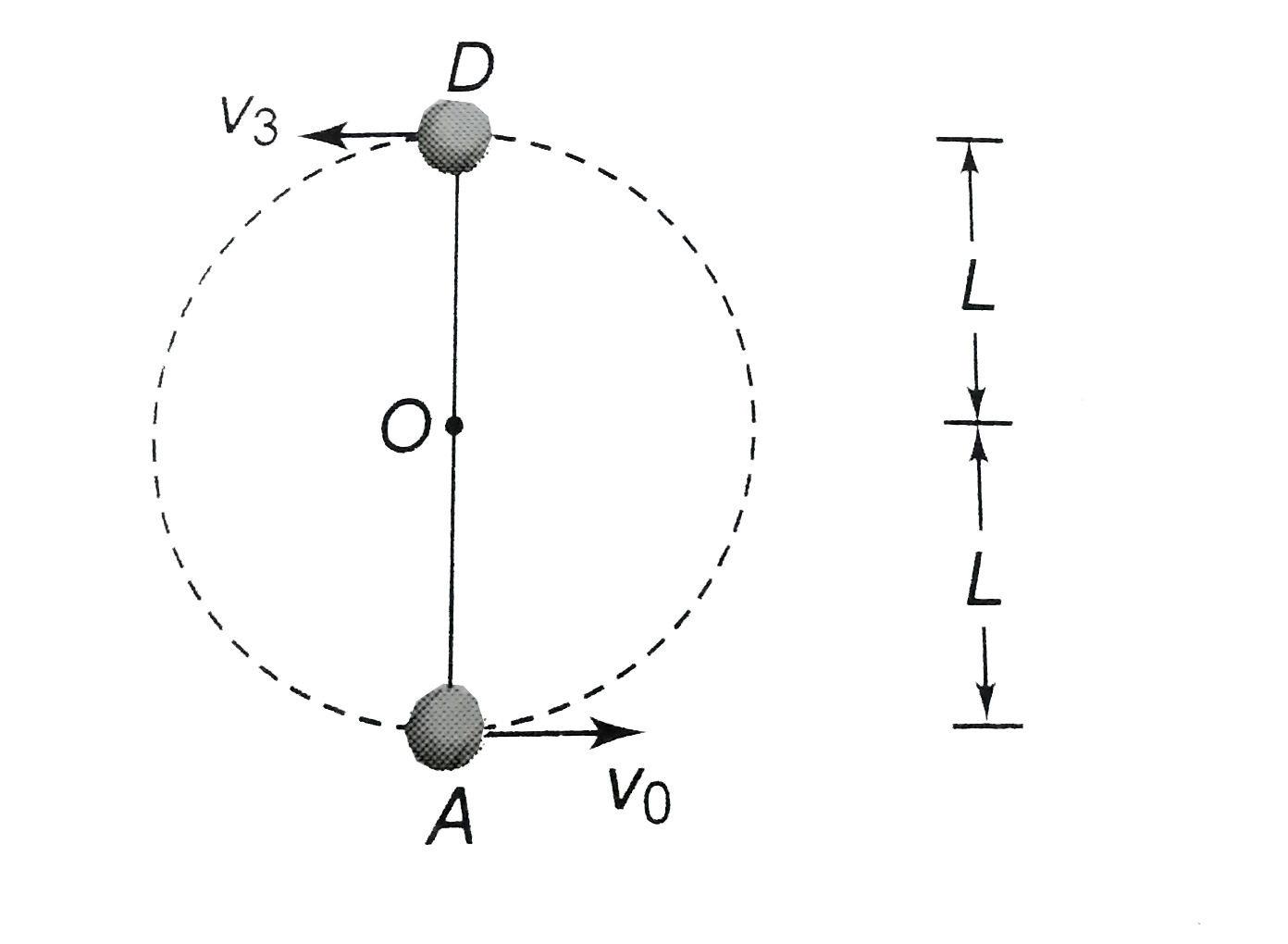
KD=12mv23,UD=mg×2L ltbegt KA+UA=KD_UD
v3=√v20−4gL
Topper's Solved these Questions
Similar Questions
A bob is attached to a string of length l whose other end is fixed and is given horizontal velocity at the lowest point of the circle so that the bob moves in a vertical plane. Match the velocity given at the lowest point of circle in column I with tension and velocity at the highest point of the circle corresponding to velocity of column I of column II

View SolutionA bob is attached to a string of length l whose other end is fixed and is given horizontal velocity at the lowest point of the circle so that the bob moves in a vertical plane. Match the velocity given at the lowest point of circle in column I with tension and velocity at the highest point of the circle corresponding to velocity of column I of column II

View Solution
Knowledge Check
A small spherical ball is suspended through a string of length l . The whole arrangement is placed in a vehicle which is moving with velocity v . Now, suddenly the vehicle stops and ball starts moving along a circular path. If tension in the string at the highest point is twice the weight of the ball then (assume that the ball completes the vertical circle)
Av=√5glBv=√7glCvelocity of the ball at highest point is √glDvelocity of the ball at highest point is √3gl
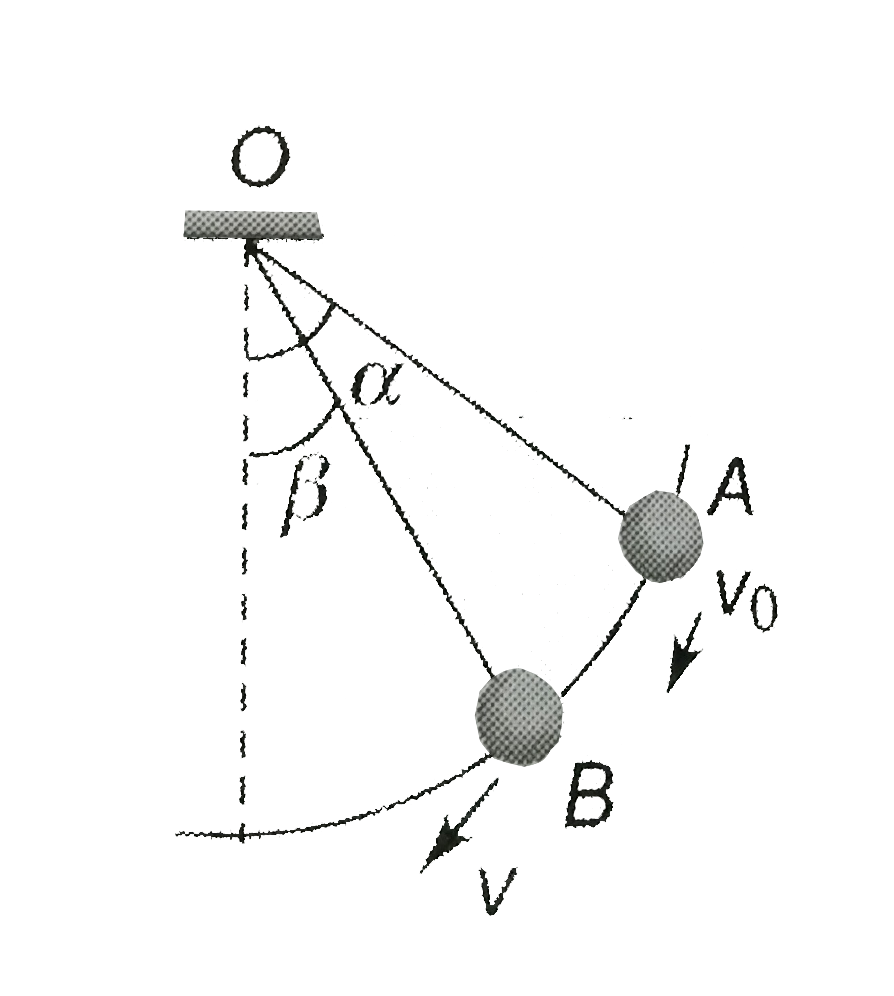
A ball attached to a string length L is oscillating line a simple pendulum. Find v in terms of v0 L α and β.
View SolutionA small spherical ball is suspended through a string of length l . The whole arrangement is placed in a vehicle which is moving with velocity v . Now, suddenly the vehicle stops and ball starts moving along a circular path. If tension in the string at the highest point is twice the weight of the ball then (assume that the ball completes the vertical circle)
View SolutionA ball of mass m is attached to a light string of length L and suspended vertically. A constant horizontal force, whose magnitude F equals the weight of the ball, is applied Determine the speed of the ball as it reaches the 90∘ level.
View Solution
A ball of mass 200g is attached to a string of length 50cm and a force F is applied on it as shown. Find the work done by this force if string makes an angle 60∘ with vertical. In the initial and final position, speed of the ball is zero.
View SolutionA ball is hanging vertically by a light inextensible string of length L from fixed point O. The ball of mass m is given a speed u at the lowest position such that it completes a vertical circle with centre at O as shown. Let AB be a diameter of circular path of ball making an angle θ with vertical as shown. (g is acceleration due to gravity)
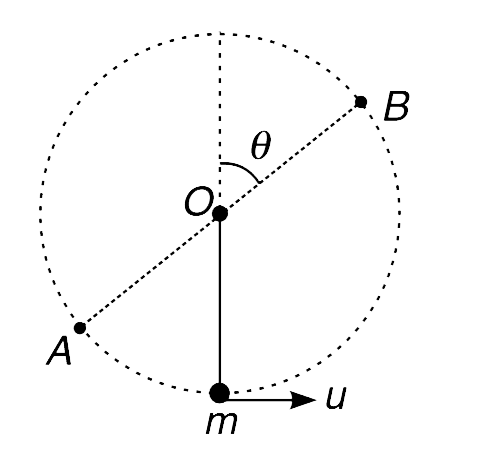
a) Let TA and TB be tension in string when ball is at A and B respectively, then find TA – TB. (b) Let →aA and →aB be acceleration of ball when it is at A and B respectively, then find the value of |→aA+→aB|
View SolutionA ball is attached to a horizontal cord of length l whose other end is fixed. (a) If the ball is released, what will be its speed at the lowest point of its path? (b) A peg is located a distance h directly below the point of attachment of the cord. If h=0.75l, what will be the speed of the ball when it reaches the top of its circular path about the peg?
View SolutionA ball is attached to a horizontal cord of length l whose other end is fixed. (a) If the ball is released, what will be its speed at the lowest point of its path? (b) A peg is located a distance h directly below the point of attachment of the cord. If h=0.75l, what will be the speed of the ball when it reaches the top of its circular path about the peg?
View Solution
