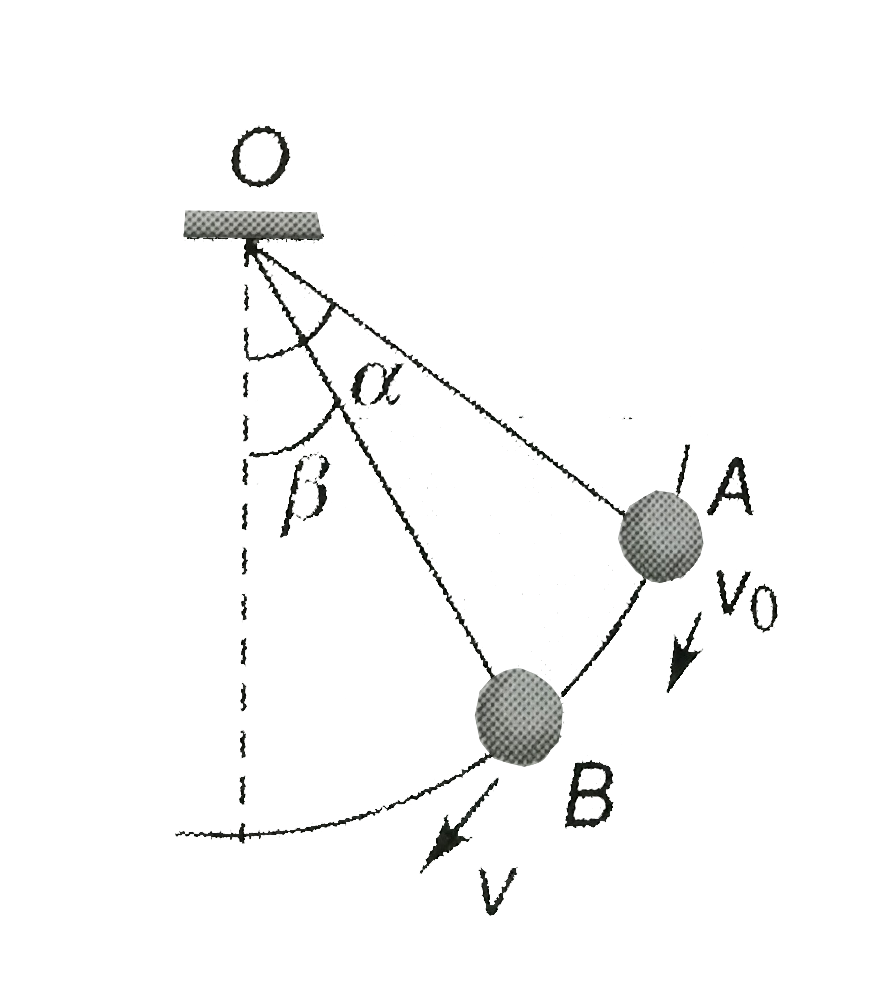
A ball attached to a string length L is oscillating line a simple pendulum. Find v in terms of v0 L α and β.
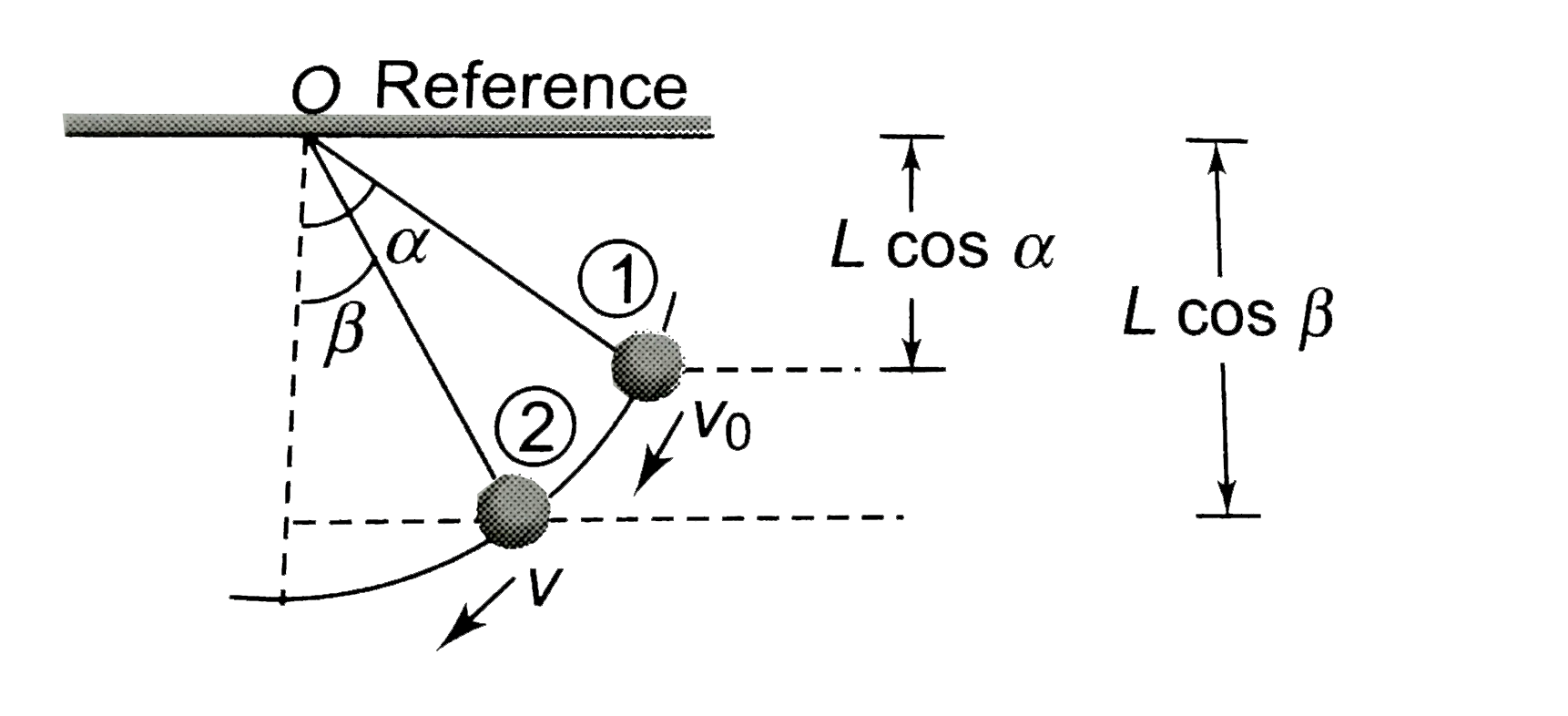
K1=12mv20,U1=−mgLcosα
K2=12mv2,U2=−mgLcosβ
K1+U1=K2+U2
12mv20−mgLcosα=12mv2−mgLcosβ
v=√v20+2gL(cosβ−cosα)
If we assume the reference line at (2), then
K1=12mv20,U1=mgL(cosβ−cosα)
K2=12mv2,U2=0
Topper's Solved these Questions
Similar Questions

A ball is attached to a string of length L and the ball is given velocity v0 at its lowest point. Find the speed of the ball at point B,C and D. Assume that the ball is moving in vertical circle.
View SolutionA ball is attached to a string of length L. The ball is released when the string is horizontal. The ball collides with wall and e=2/√5. After how many minimum number of collisions , the amplitude of oscillation becomes less than 60∘.

View Solution
Knowledge Check
For a conical pendulum of string length L, its angular speed is proportional to
A√LBLC1√LD1LThe graph between time period (T) and length (l) of a simple pendulum is
A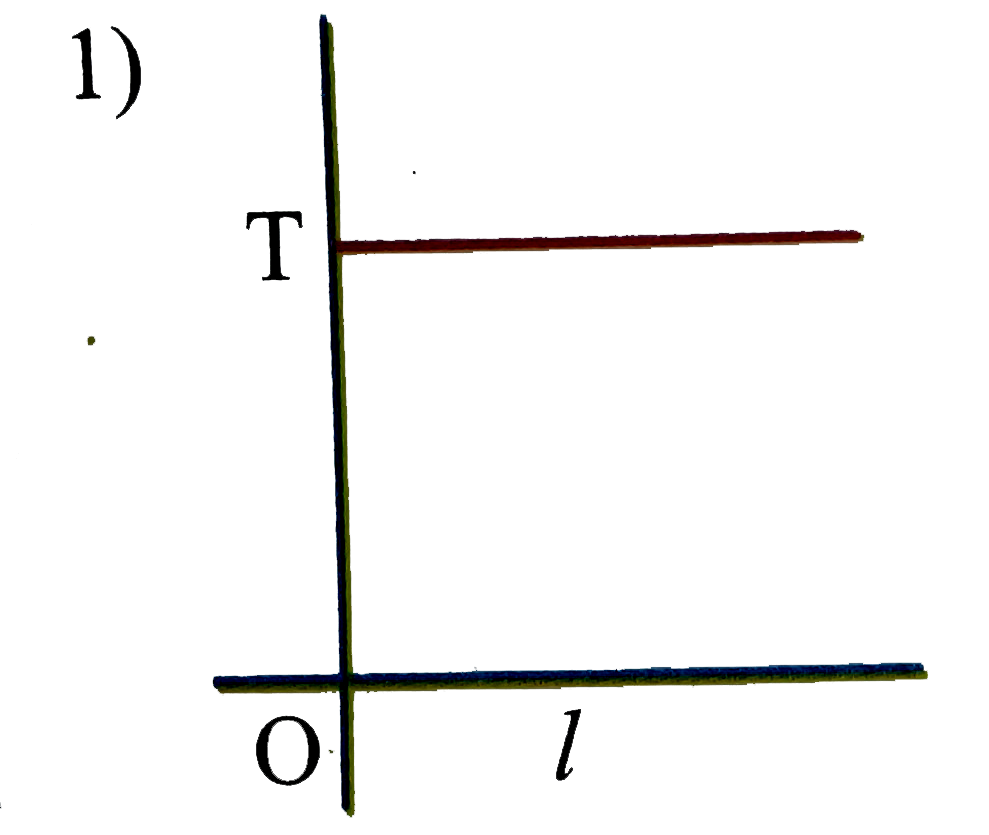 B
B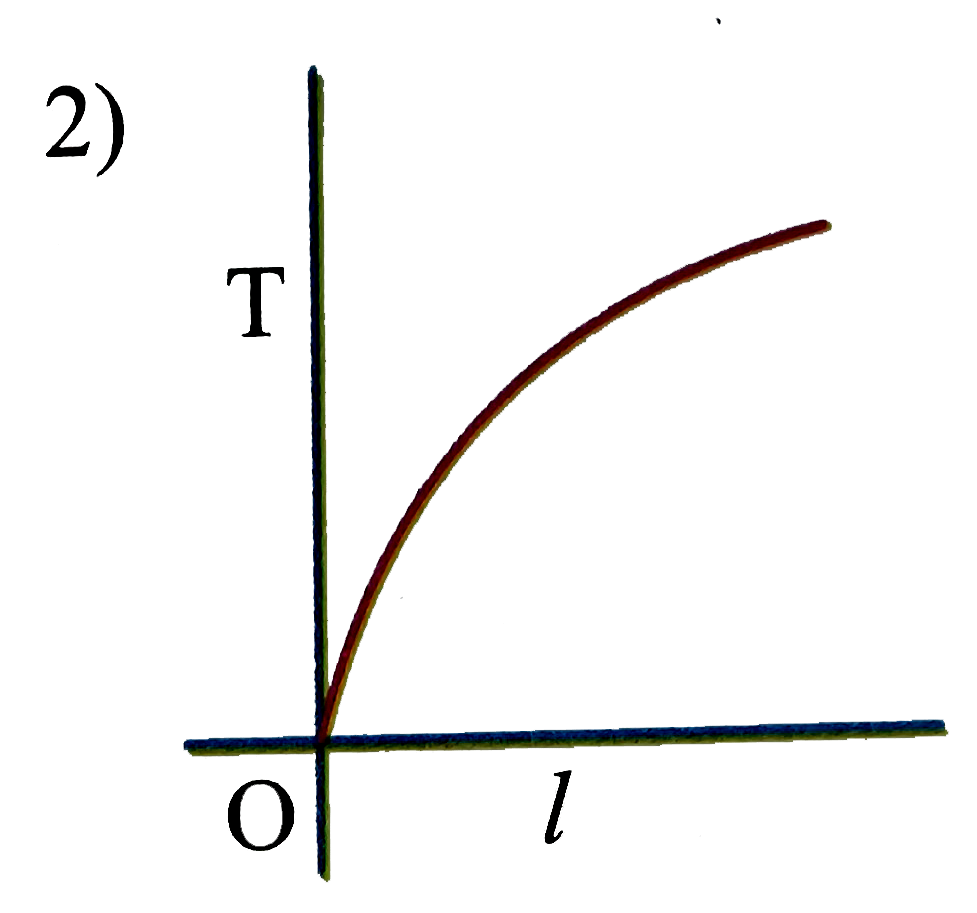 C
C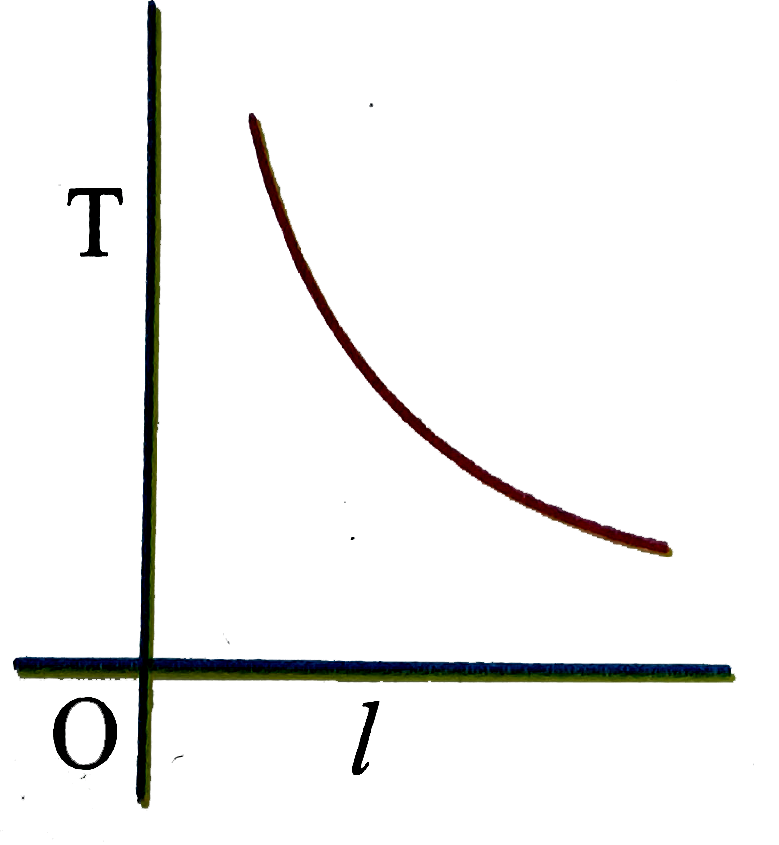 D
D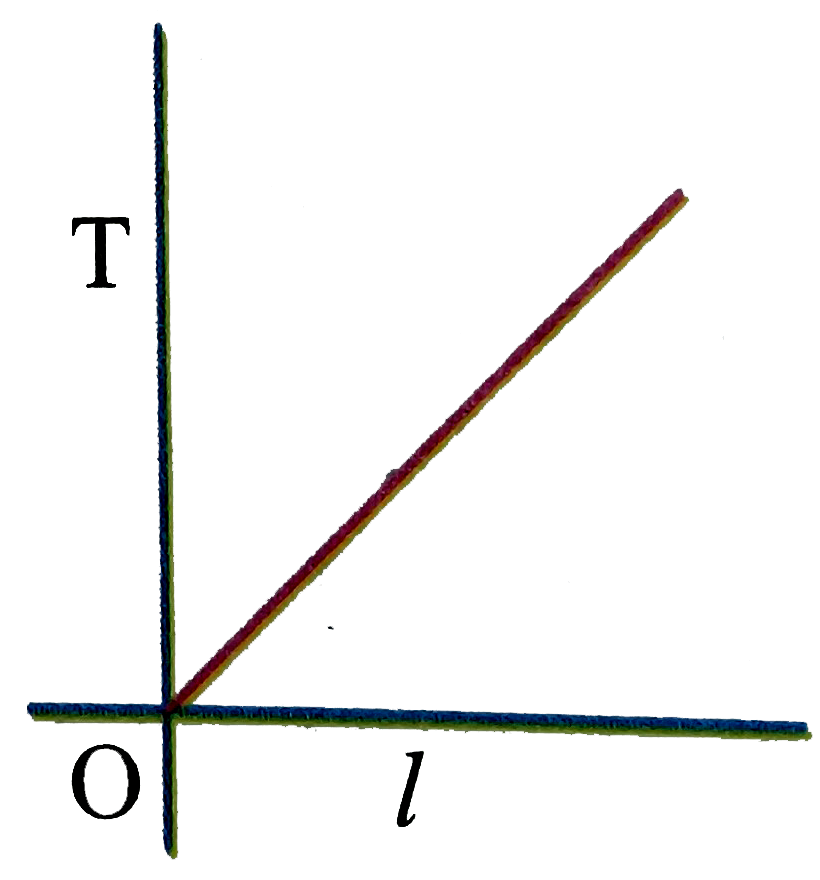
A simple pendulum consisting of a mass M attached to a string of length L is released from rest at an angle α. A pin is located at a distance l below the pivot point. When the pendulum swings down, the string hits the pin as shown in figure. The maximum angle θ which the string makes with the vertical after hitting the pin is
 A(a) cos−1[Lcosα+lL+l]B(b) cos−1[Lcosα+lL−l]C(c) cos−1[Lcosα−1L−l]D(d) cos−1[Lcosα−1L+l]
A(a) cos−1[Lcosα+lL+l]B(b) cos−1[Lcosα+lL−l]C(c) cos−1[Lcosα−1L−l]D(d) cos−1[Lcosα−1L+l]
(i) A simple pendulum consist of a small bob of mass m tied to a string of length L. Show that the total energy of oscillation of the pendulum is E≅12mgLθ20 when it is oscillating with a small angular amplitude θ0. Assume the gravitational potential energy to be zero of the lowest position of the bob. (ii) Three identical pendulums A, B and C are suspended from the ceiling of a room. They are swinging in semicircular arcs in vertical planes. The string of pendulum A snaps when it is vertical and it was found that the bob fell on the floor with speed V1. The string of B breaks when it makes an angle of 30° to the vertical and the bob hits the floor with speed V2. The string of pendulum C was cut when it was horizontal and the bob falls to the floor hitting it with a speed V3. Which is greatest and which is smallest among V1,V2 and V3?
View SolutionA ball A of mass m attached to a string of length L is released when the string is horizontal. It strikes another ball B of mass 2m suspended to another string of length L at rest as shown. Find the maximum angle made by the string if the collision is completely inelastic.
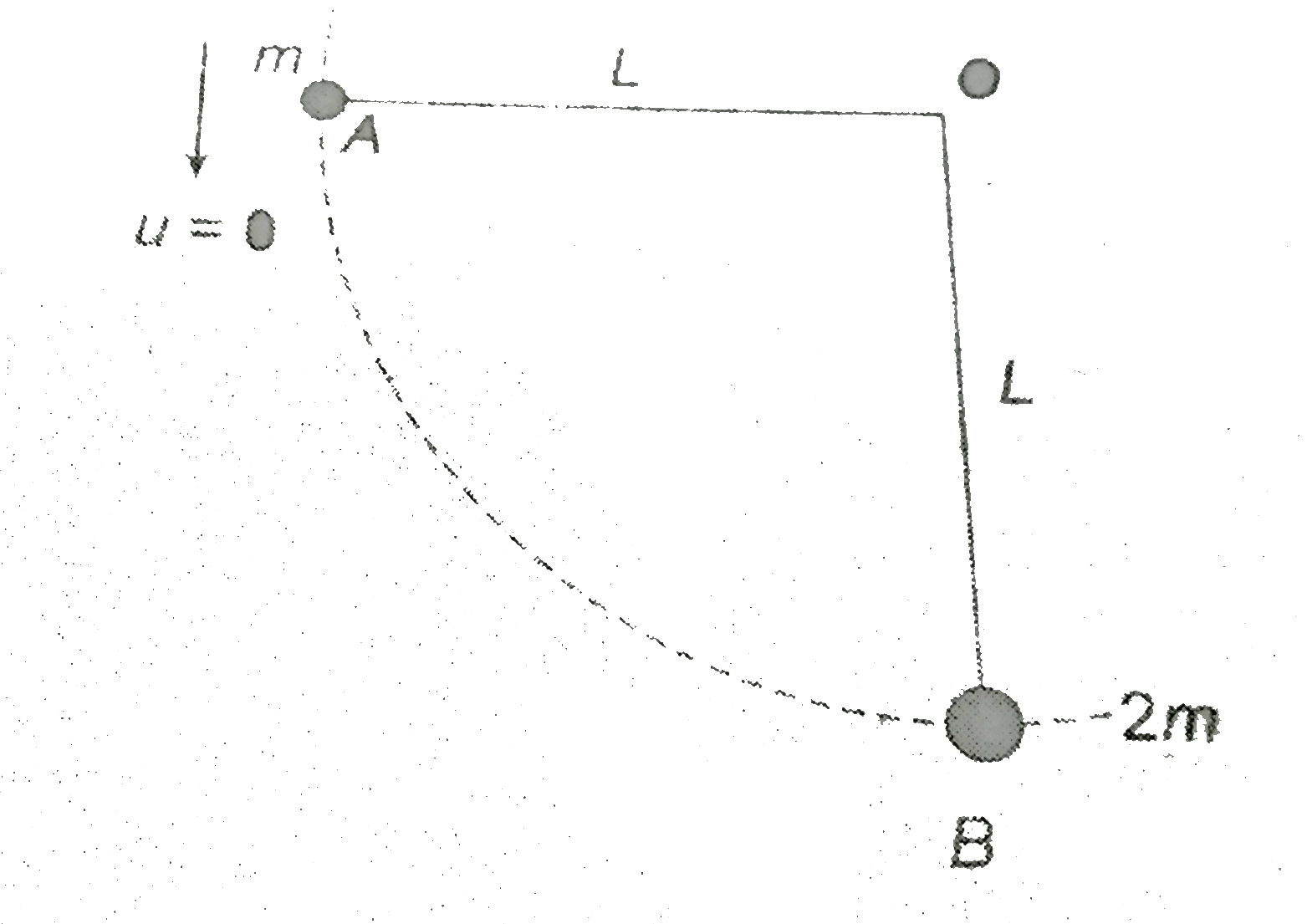
View SolutionA uniform rod of length l is suspended by end and is made to undego small oscillations. Find the length of the simple pendulum having the time period equal to that of the rod.
View SolutionA ball of mass m kept at the centre of a string of length L is pulled from centre in perpendicular direction and released. Prove that motion of ball is simple harmonic and determine time period of oscillation
View SolutionConsider a simple pendulum having a bob attached to a string that oscillates under the action of a force of gracity. Suppose that the period of oscillation of the simple pendulum depends on its length (I), mass of the bob (m) and acc. Due to gravity (g). Derive the expression for its time period using method of dimensions.
View Solution
