A particle is placed at the origin and a force F=Kx is acting on it (where k is a positive constant). If U(0)=0, the graph of U(x) verses x will be (where U is the potential energy function.)
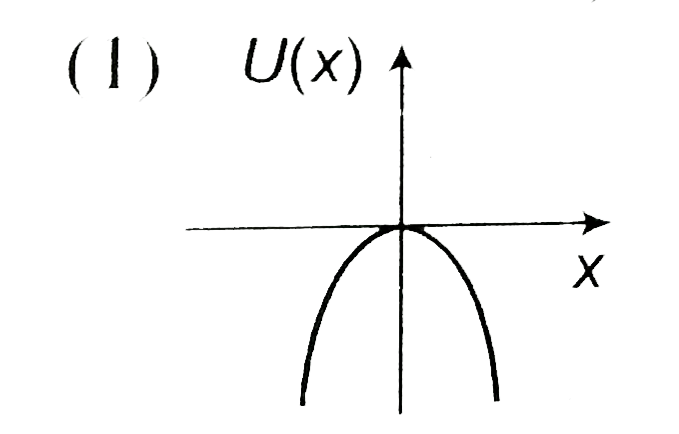
The correct Answer is:A
F=kx
U=−∫x0Fdx=−∫x0kxdx=−12kx2
U v/s x graph will be a parabola, open downward
Topper's Solved these Questions
Similar Questions
A particle, which is constrained to move along x-axis, is subjected to a force in the some direction which varies with thedistance x of the particle from the origin an F(x)=−kx+ax3. Here, k and a are positive constants. For x(≥0, the functional form of the potential energy (u) U of the U (x) the porticle is.
(a)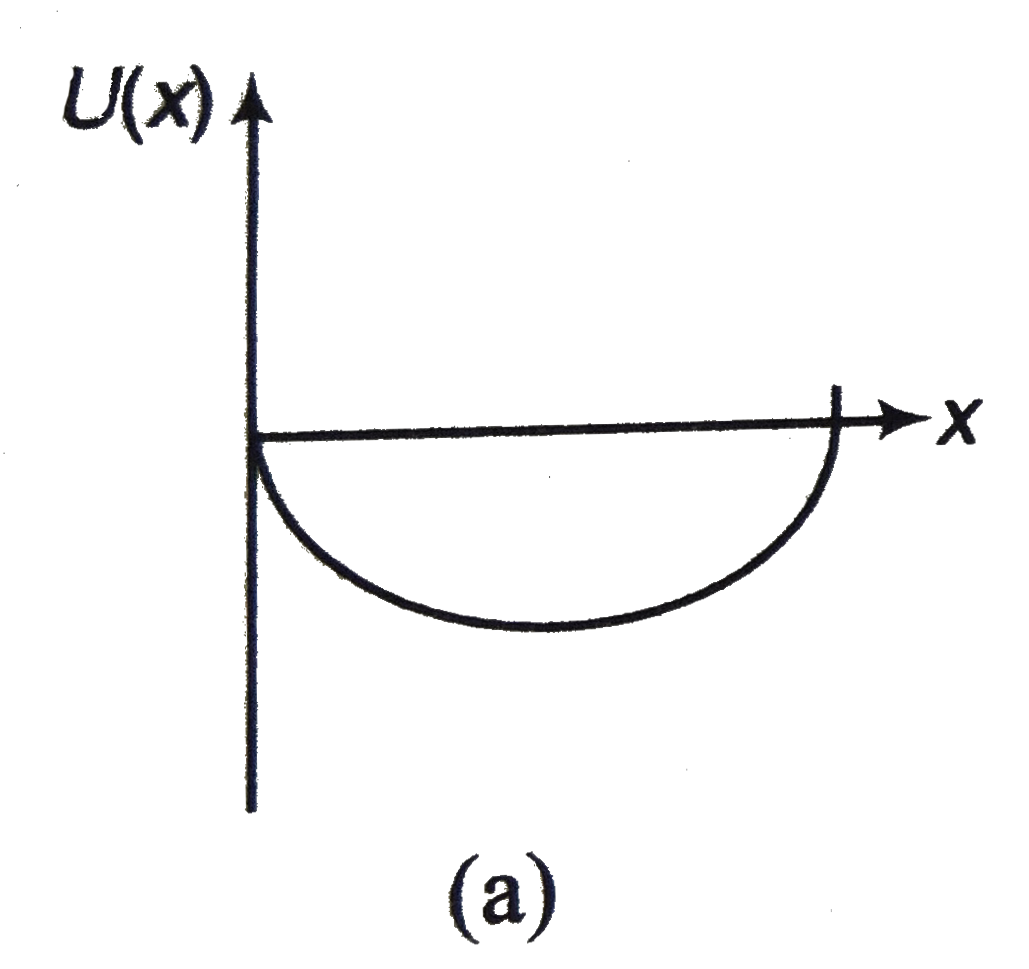 , (b)
, (b) 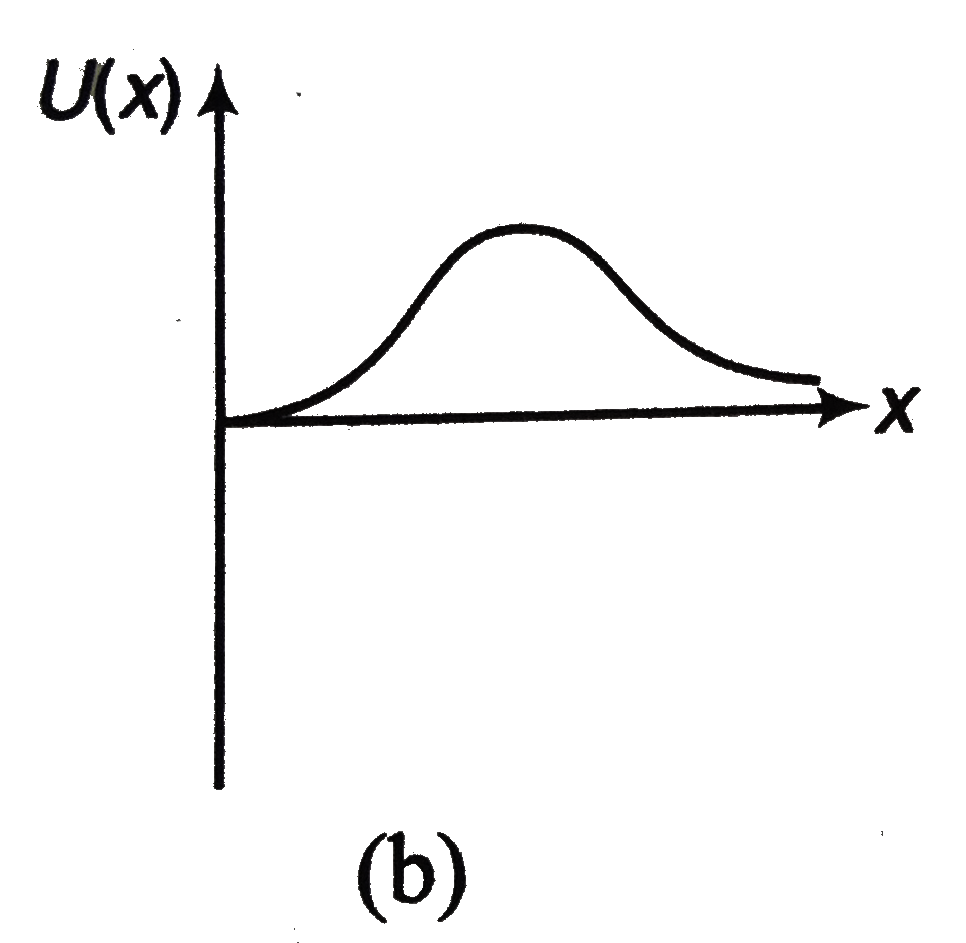 , (c)
, (c) 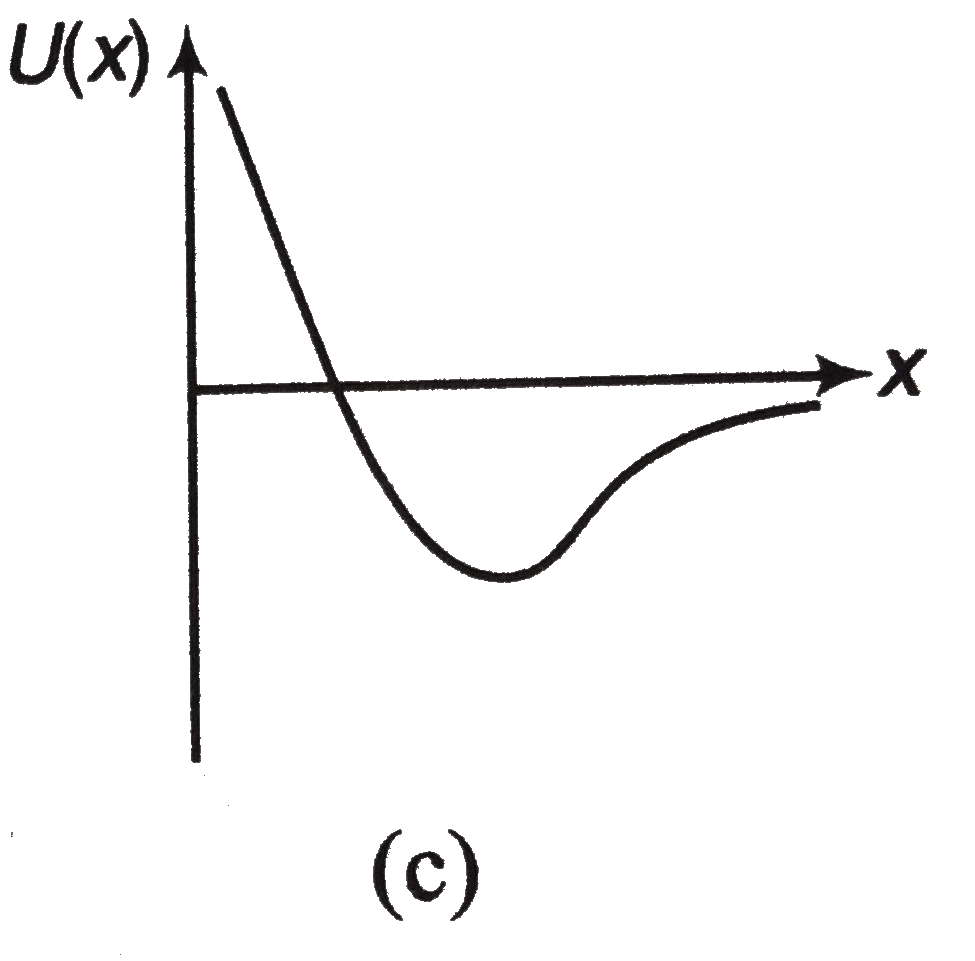 , (d)
, (d) 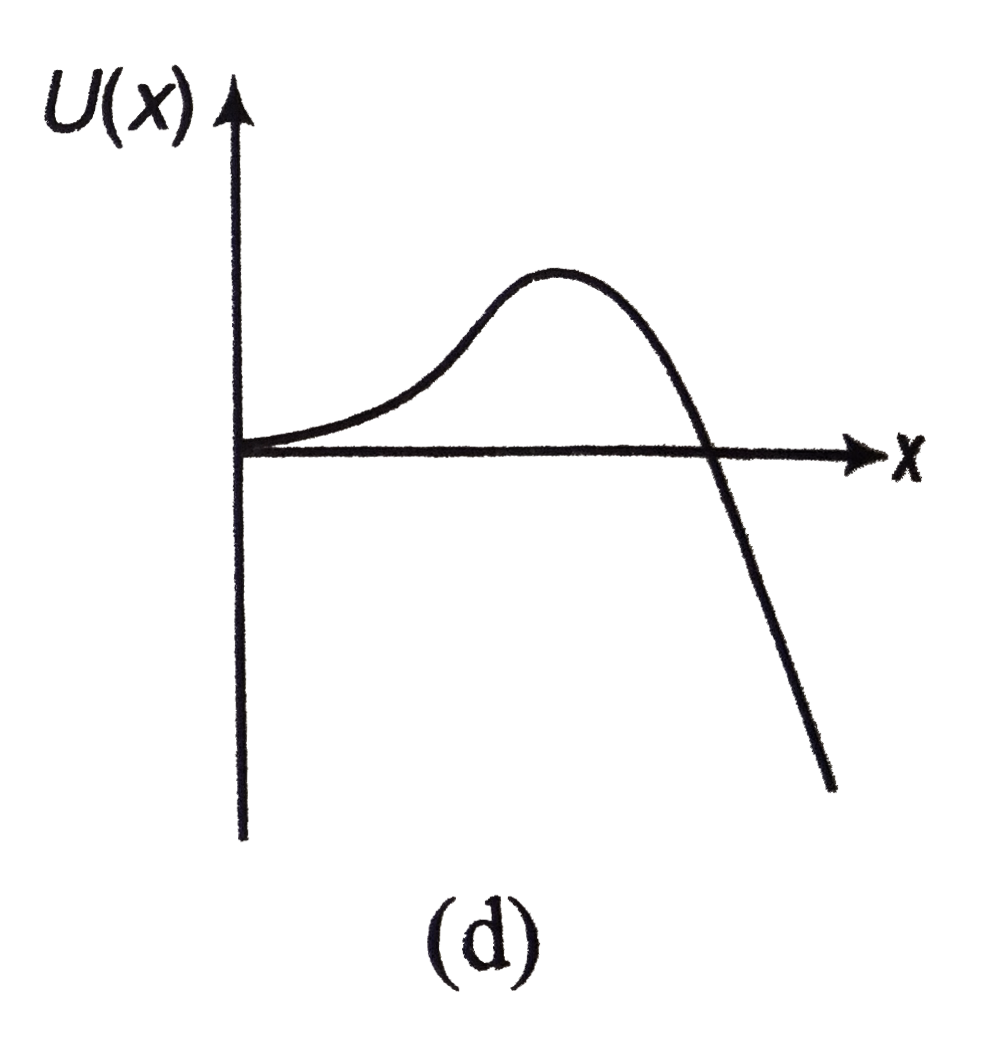 . View Solution
. View SolutionThe potential energy of configuration changes in x and y directions as U=kxy, where k is a positive constant. Find the force acting on the particle of the system as the function of x and y.
View Solution
Knowledge Check
- Question 1 - Select One
A particle is placed at the origin and a force F=Kx is acting on it (where k is a positive constant). If U(0)=0, the graph of U(x) verses x will be (where U is the potential energy function.)
A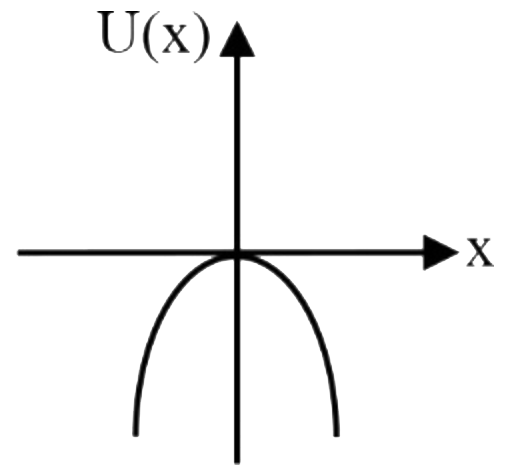 B
B C
C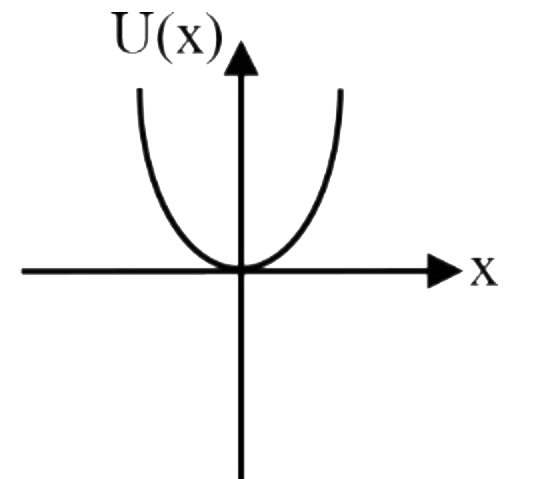 D
D
- Question 2 - Select One
A particle is placed at the origin and a force F=Kx is acting on it (where k is a positive constant). If U(0)=0, the graph of U(x) verses x will be (where U is the potential energy function.)
A B
B C
C D
D
- Question 3 - Select One
On a particle placed at origin a variable force F=−ax(where a is a positive constant) is applied. If U(0)=0, the graph between potential energy of particle U(x) and x is best represented by:-
A B
B C
C D
D
A particle of mass m is executing osciallations about the origin on the x-axis with amplitude A. its potential energy is given as U(x)=αx4, where α is a positive constant. The x-coordinate of mass where potential energy is one-third the kinetic energy of particle is
View SolutionA particle free to move along x-axis is acted upon by a force F=−ax+bx2whrteaandbarepositiveconstants.For ximplies0, the correct variation of potential energy function U(x) is best represented by.
View SolutionA particle of mass m is executing oscillations about the origin on the x-axis, it's potential energy is U(x)=k|x|2, where k is a positive constant, if the amplitude of oscillation is a, then it's time period T is
View SolutionThe potential energy U for a force field →F is such that U=−kxy where K is a constant . Then
View SolutionA particle which is constant to move along the x−aξs , is subjected to a force in the same direction which varies with the distance x of the particle from the origin as F(x)=−Kx+ax3 . Hero K and a are positive constant . For x≥0, the fanctional from of the patential every U(x) of the particle is
View Solution

