A particle free to move along x-axis is acted upon by a force For ximplies0, the correct variation of potential energy function U(x) is best represented by.
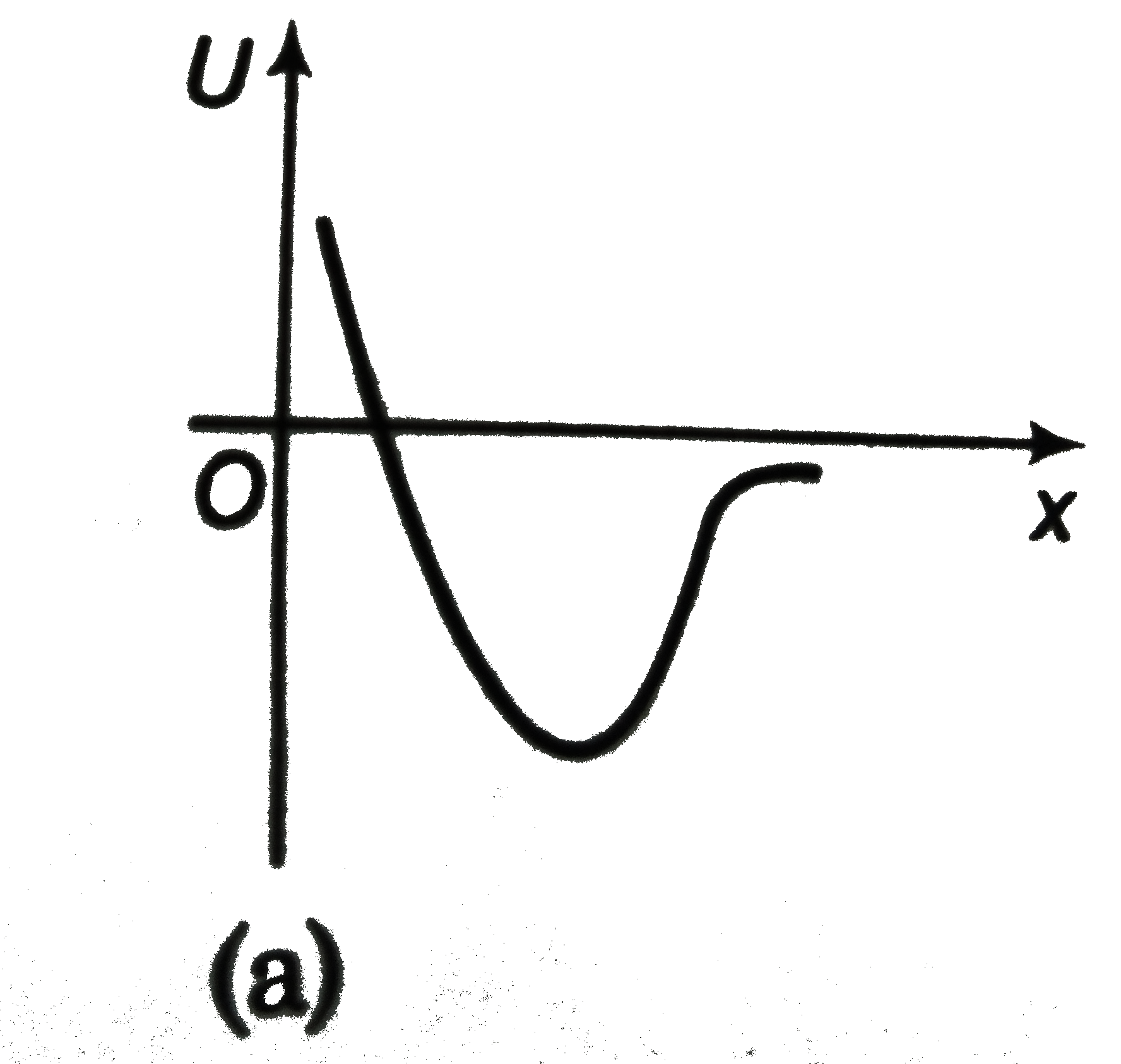
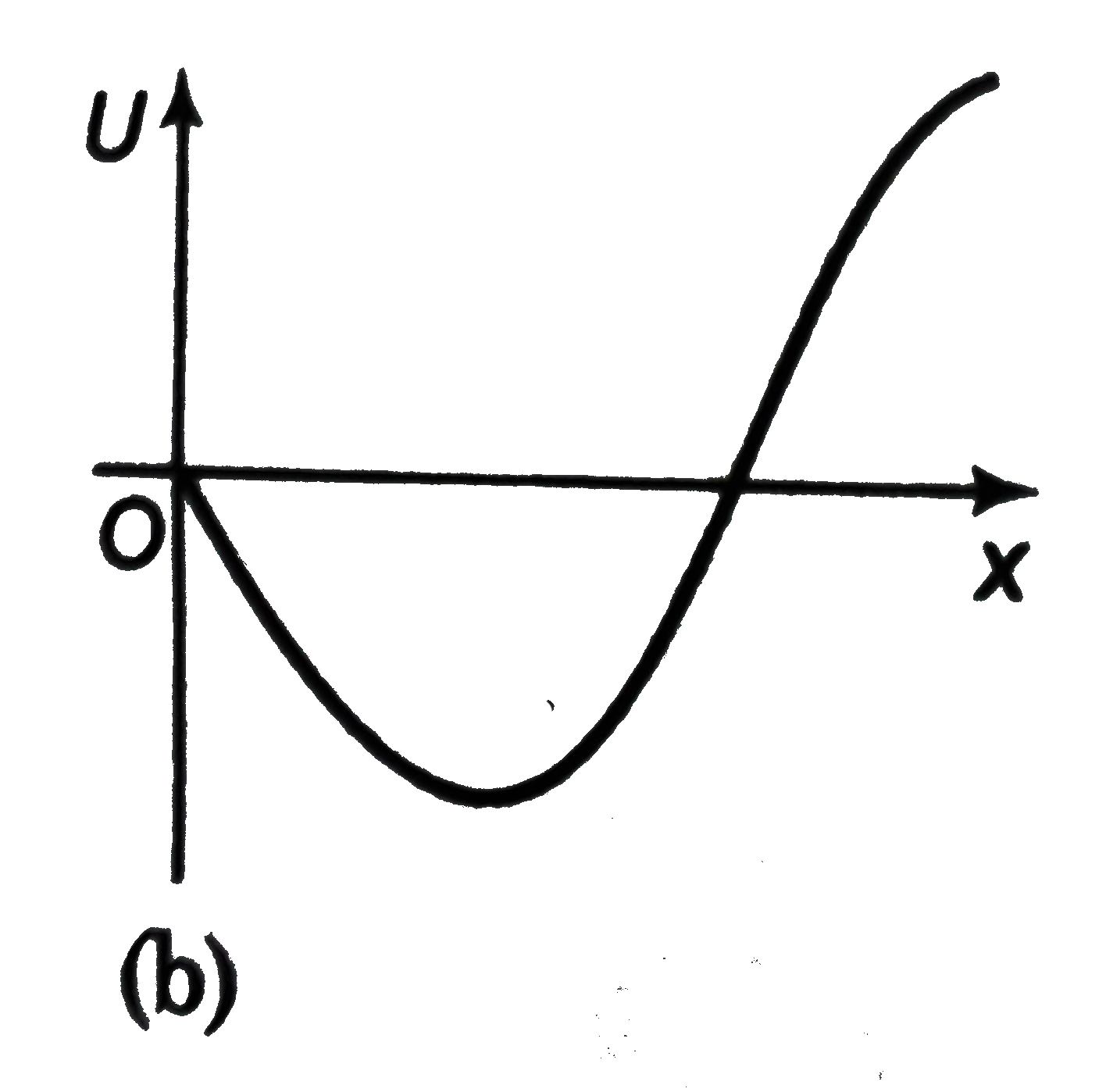
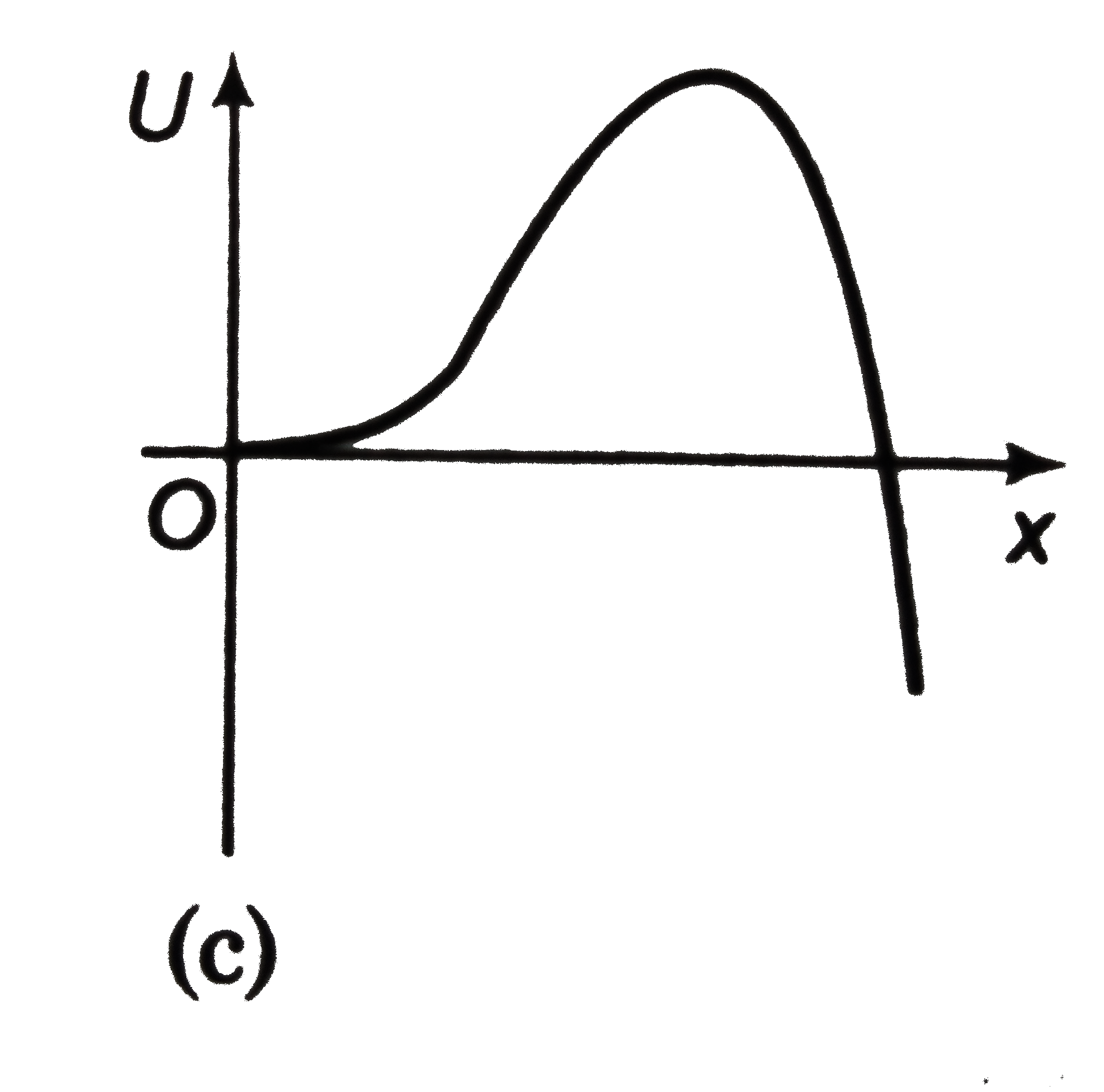
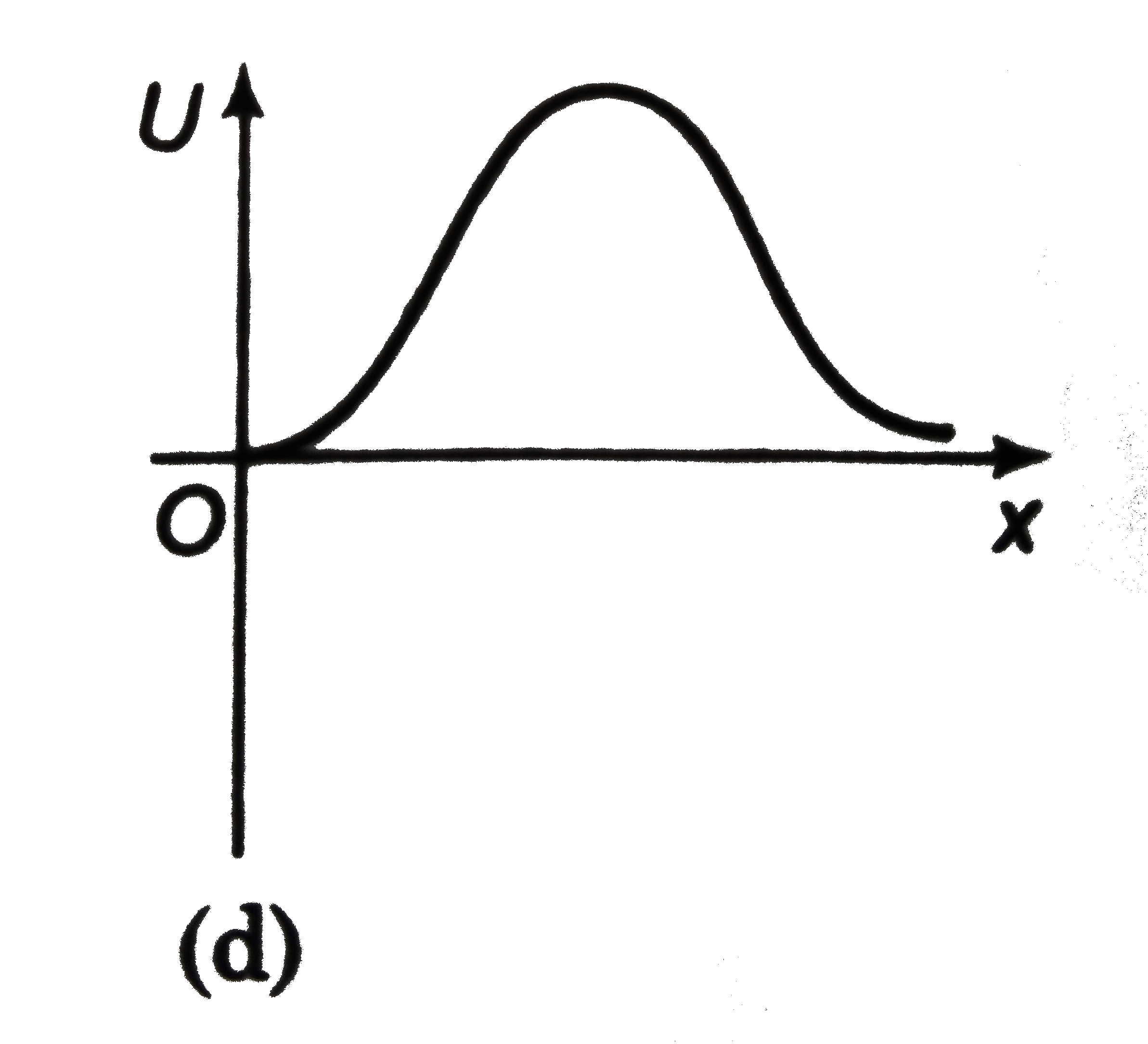
The correct Answer is:C
or
Assuning at , and integrating the above equation we get,
at and
For and U will become negative. So, option (c) is the most approprite answer.
Similar Questions
A particle, which is constrained to move along x-axis, is subjected to a force in the some direction which varies with thedistance x of the particle from the origin an F(x)=−kx+ax3. Here, k and a are positive constants. For x(≥0, the functional form of the potential energy (u) U of the U (x) the porticle is.
(a)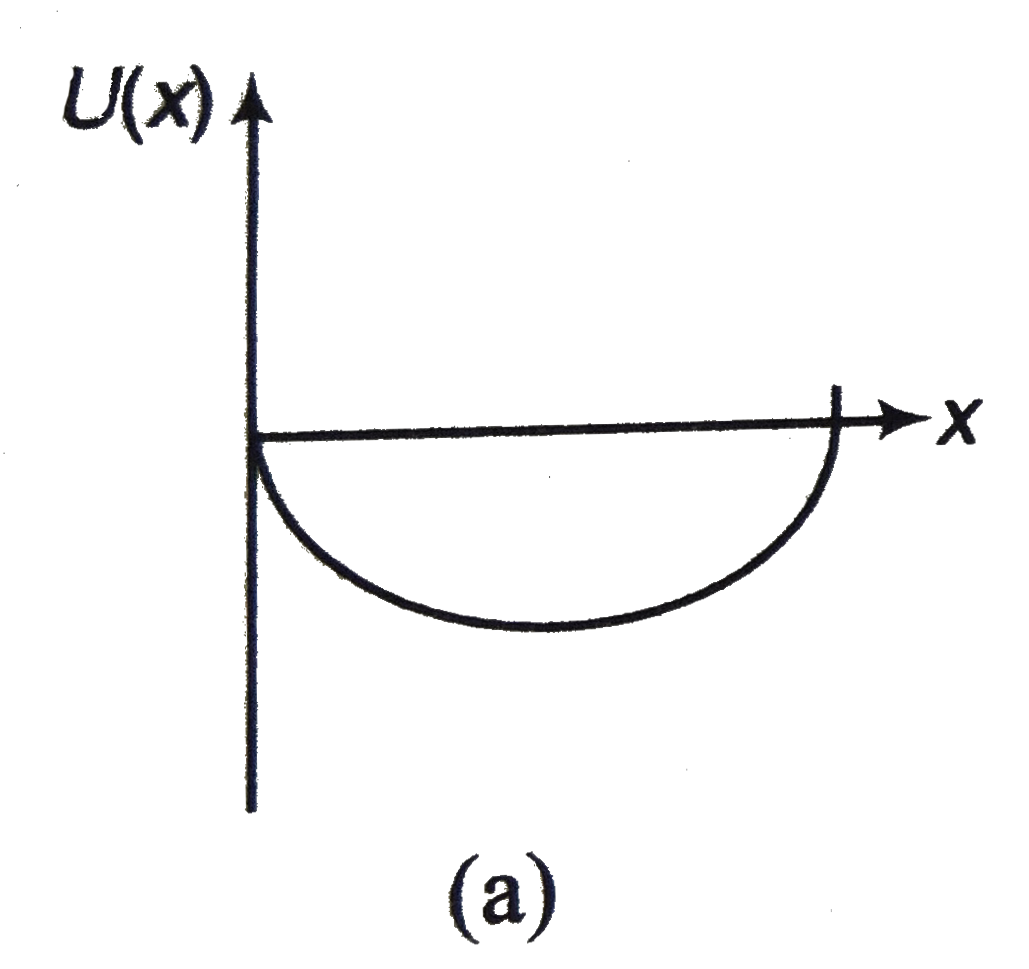 , (b)
, (b) 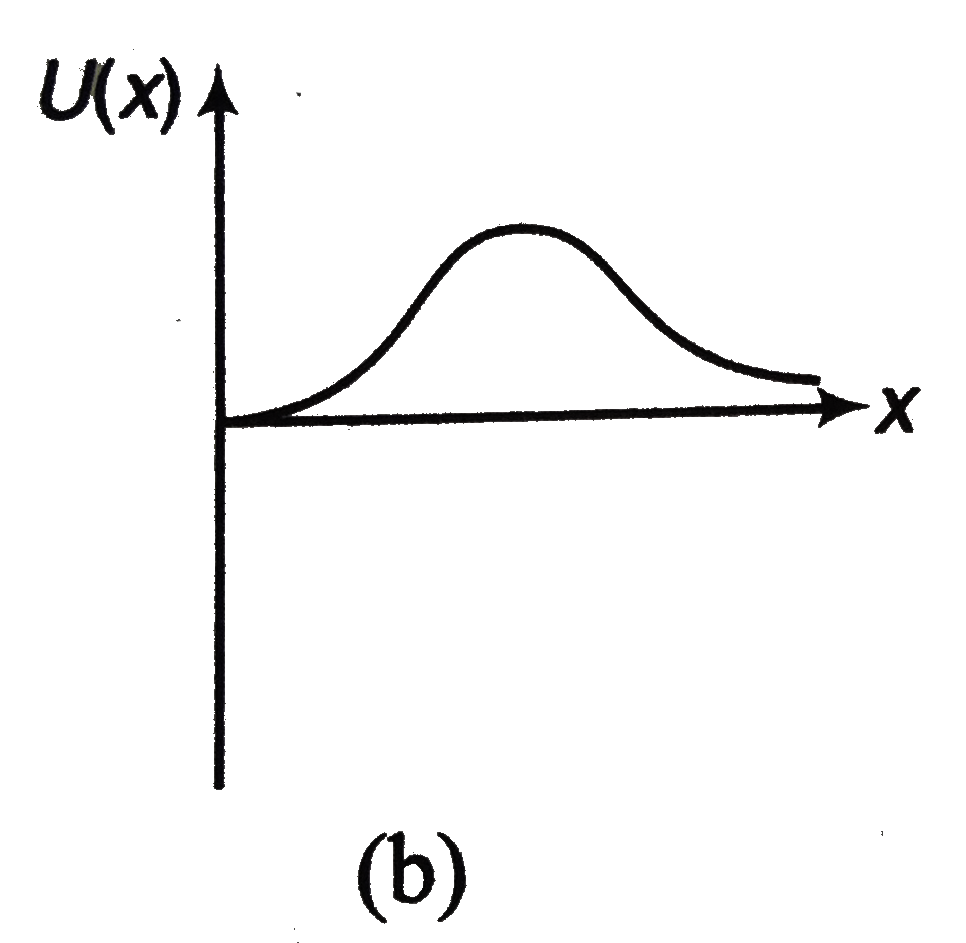 , (c)
, (c) 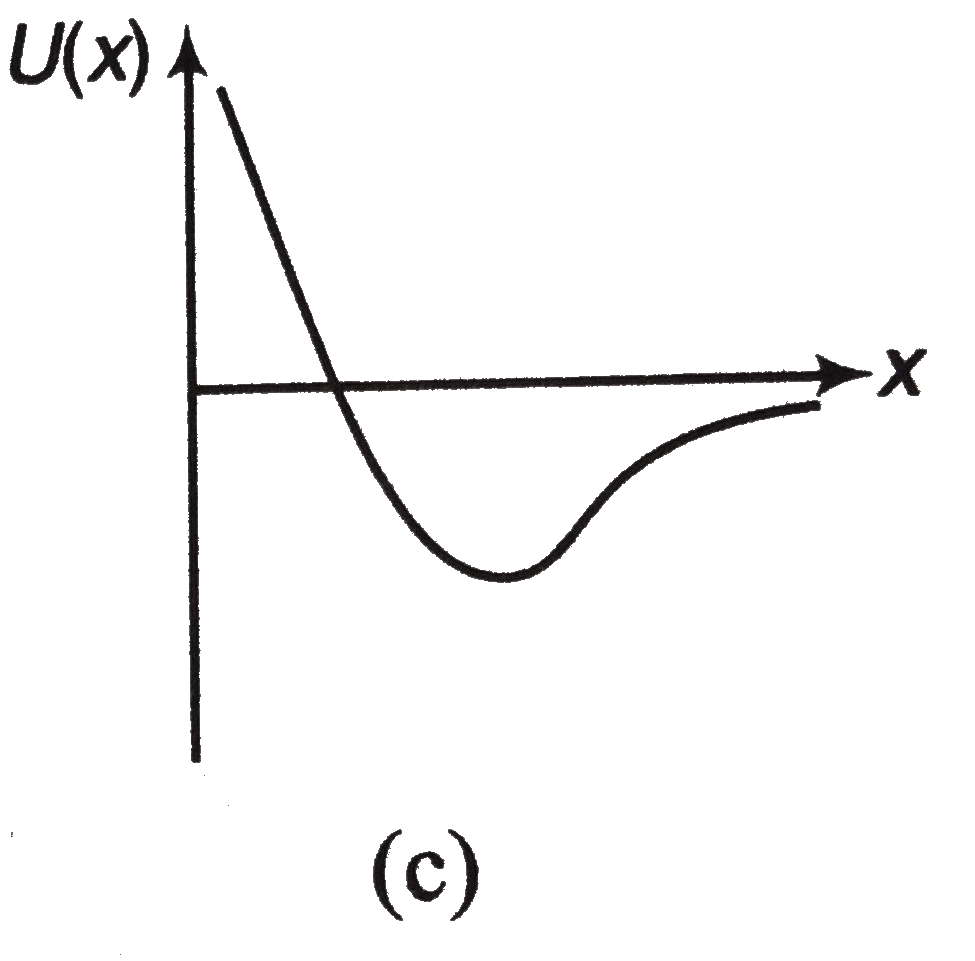 , (d)
, (d) 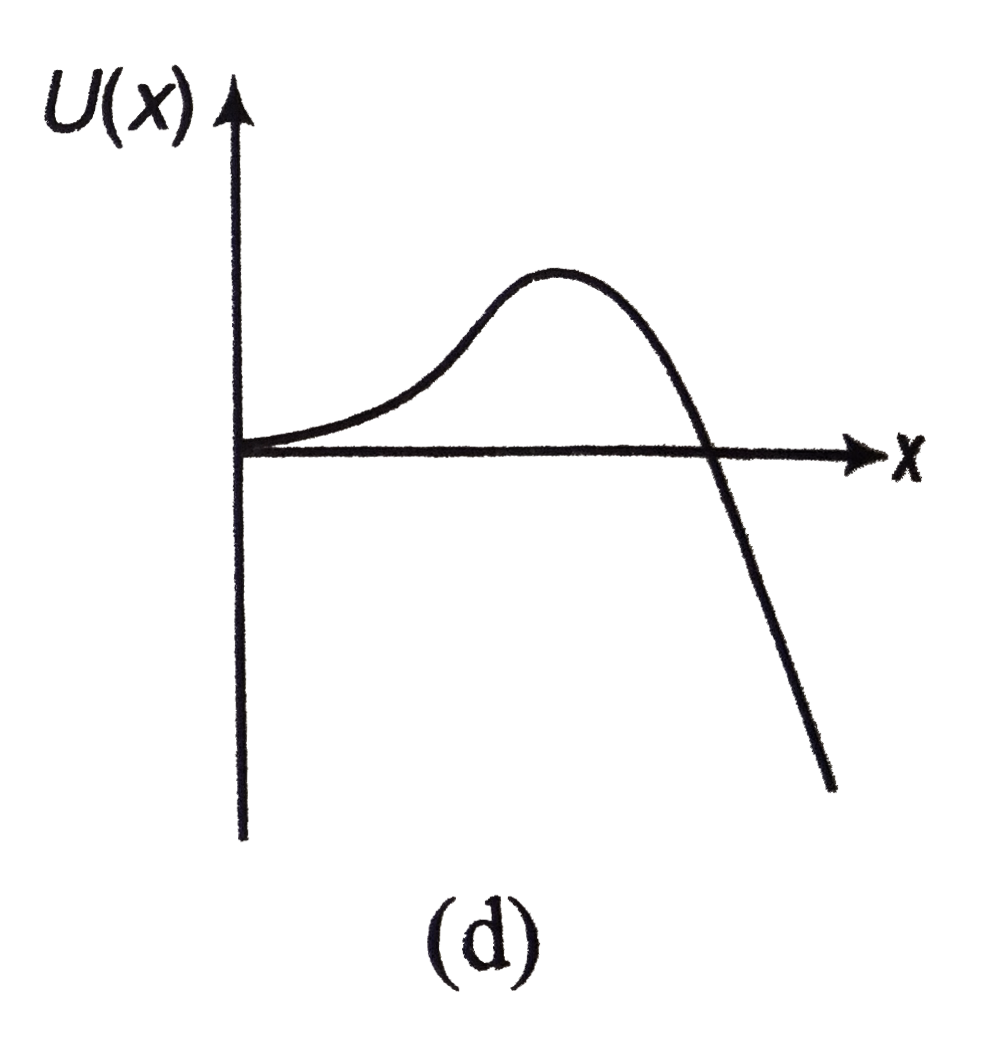 .
.
View SolutionA particle which is constant to move along the x−aξs , is subjected to a force in the same direction which varies with the distance x of the particle from the origin as F(x)=−Kx+ax3 . Hero K and a are positive constant . For x≥0, the fanctional from of the patential every U(x) of the particle is
View Solution
Knowledge Check
On a particle placed at origin a variable force F=−ax(where a is a positive constant) is applied. If U(0)=0, the graph between potential energy of particle U(x) and x is best represented by:-
A B
B C
C D
D
A particle is acted upon by a force given by F=−αx3−βx4 where α and β are positive constants. At the point x = 0, the particle is –
AIn stable equilibriumBIn unstable equilibriumCIn neutral equilibriumDNot in equilibriumA particle, which is constrained to move along the x-axis, is subjected to a force from the origin as F(x)=−kx+ax3. Here k and a are origin as F(x)=−kx+ax3. Here k and a are positive constants. For x=0, the functional form of the potential energy U(x) of particle is.
A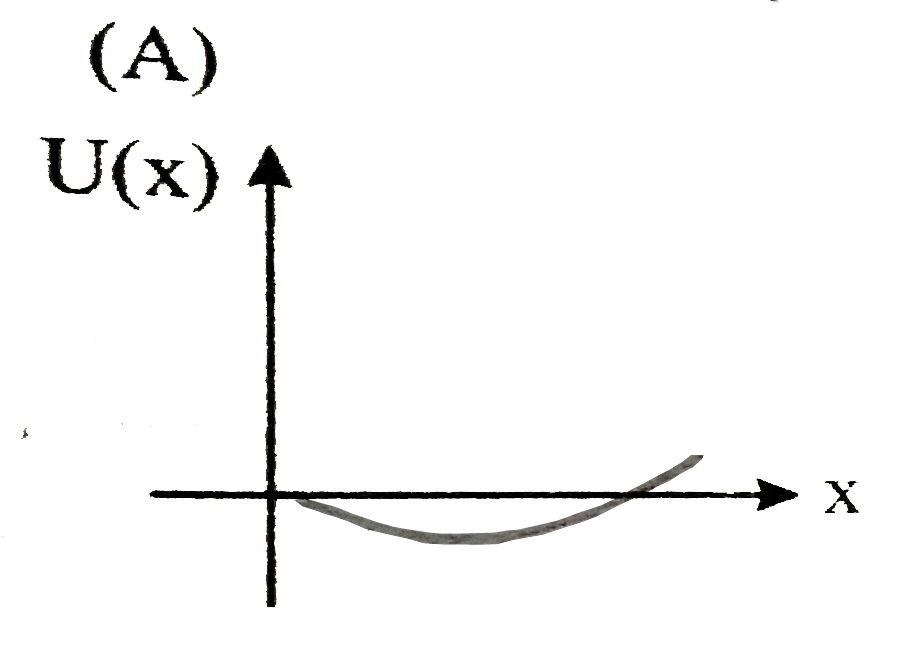 B
B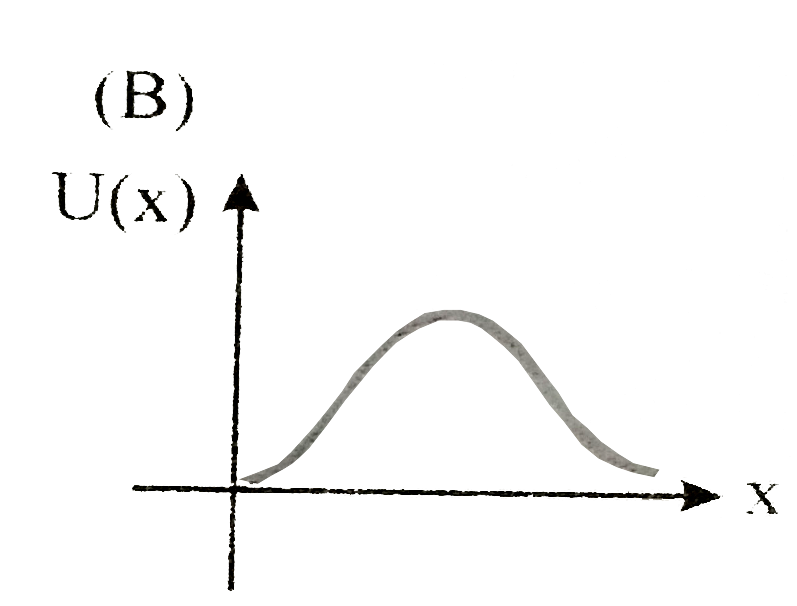 C
C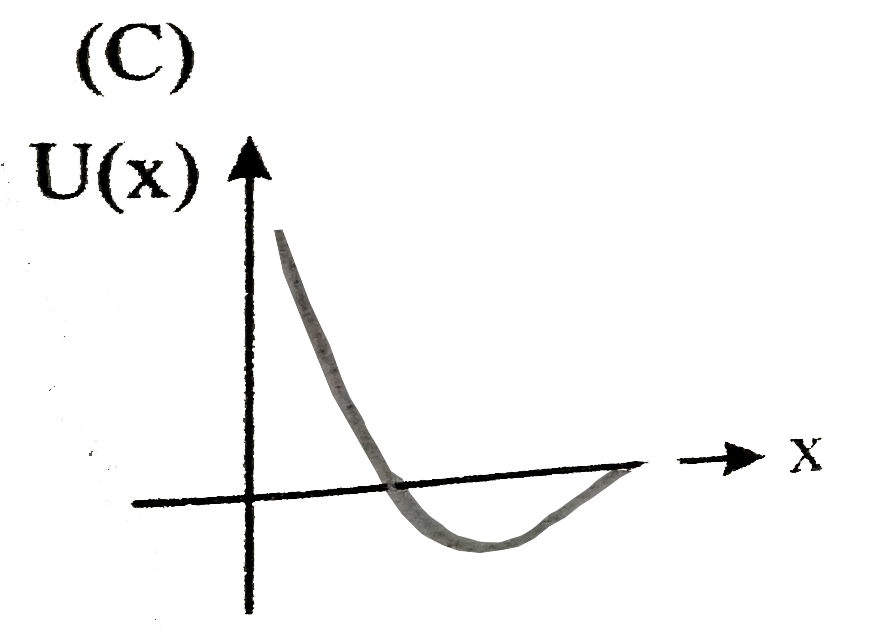 D
D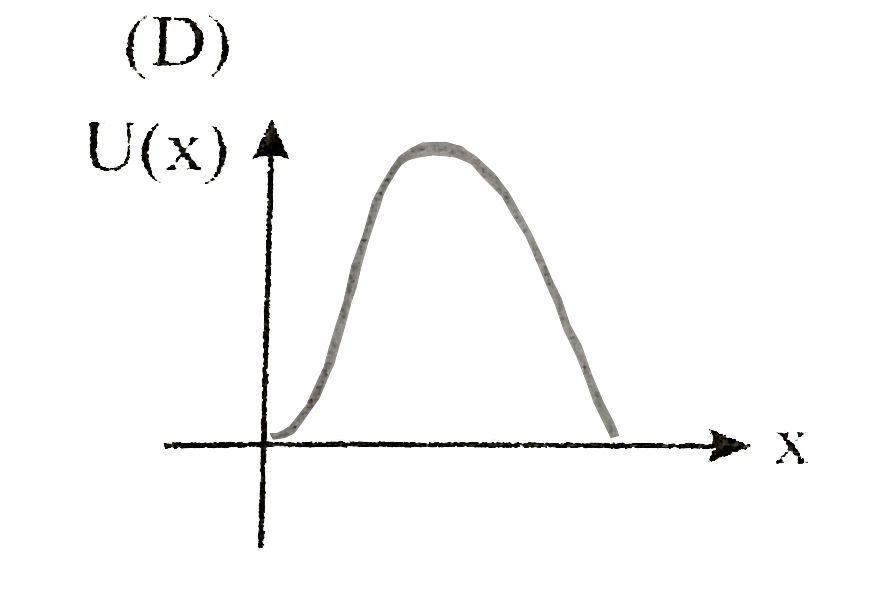
A particle of mass m moving along x-axis has a potential energy U(x)=a+bx2 where a and b are positive constant. It will execute simple harmonic motion with a frequency determined by the value of
View SolutionA particle which is constant to move along the x−aξs , is subjected to a force in the same direction which varies with the distance x of the particle from the origin as F(x)=−Kx+ax3 . Hero K and a are positive constant . For x≥0, the fanctional from of the patential every U(x) of the particle is
View SolutionA particle moving along the x axis is acted upon by a single force F = F0e−kx , where F0 and k are constants. The particle is released from rest at x = 0. It will attain a maximum kinetic energy of :
View SolutionThe potential energy U=3ax3−2bx2. The force constant is represented by
View SolutionA particle which is constant to move along the x−aξs , is subjected to a force in the same direction which varies with the distance x of the particle from the origin as F(x)=−Kx+ax3 . Hero K and a are positive constant . For x≥0, the fanctional from of the patential every U(x) of the particle is
View Solution
