Three identical roads each of mass $M$ and $L$ are joined to form an equilateral triangle. Find the $M . I .$ about an axis perpendicular to the plane of triangle and passing through
( $a$ ) center of triangle
( $b$ ) mid-point of a rod and
( $c$ ) one vertex of triangle.

Video Solution

Text Solution

Verified by Experts

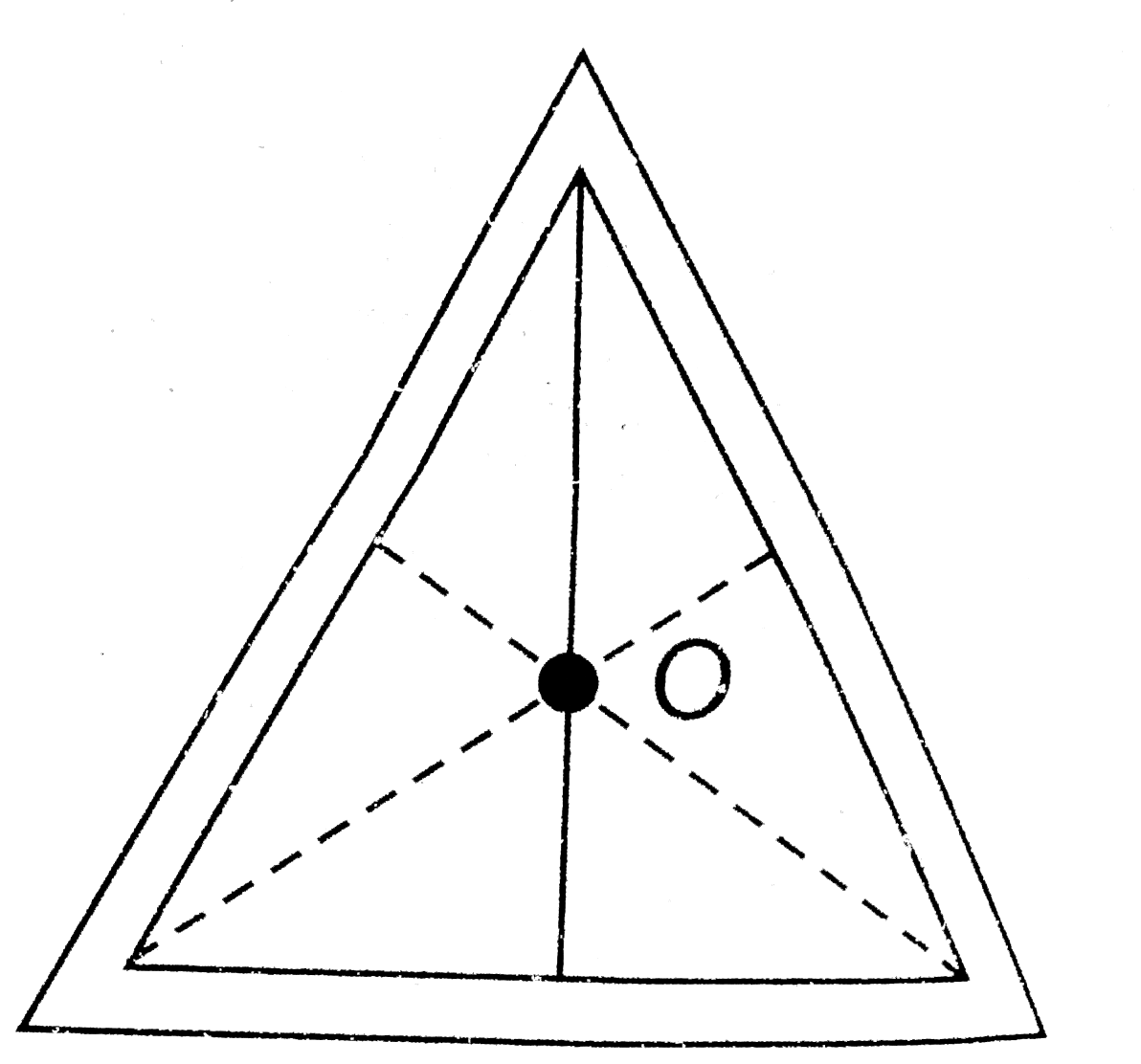
( $a$ ) Axis is passing through $O$ and $⊥^{a r}$ to the plane. $M . I .$ of rod ( $1$ ), about and axis passing through $D$ and $⊥^{a r}$ to the length ( $⊥^{a r}$ to the plane) $= \frac{M L^{2}}{12}$

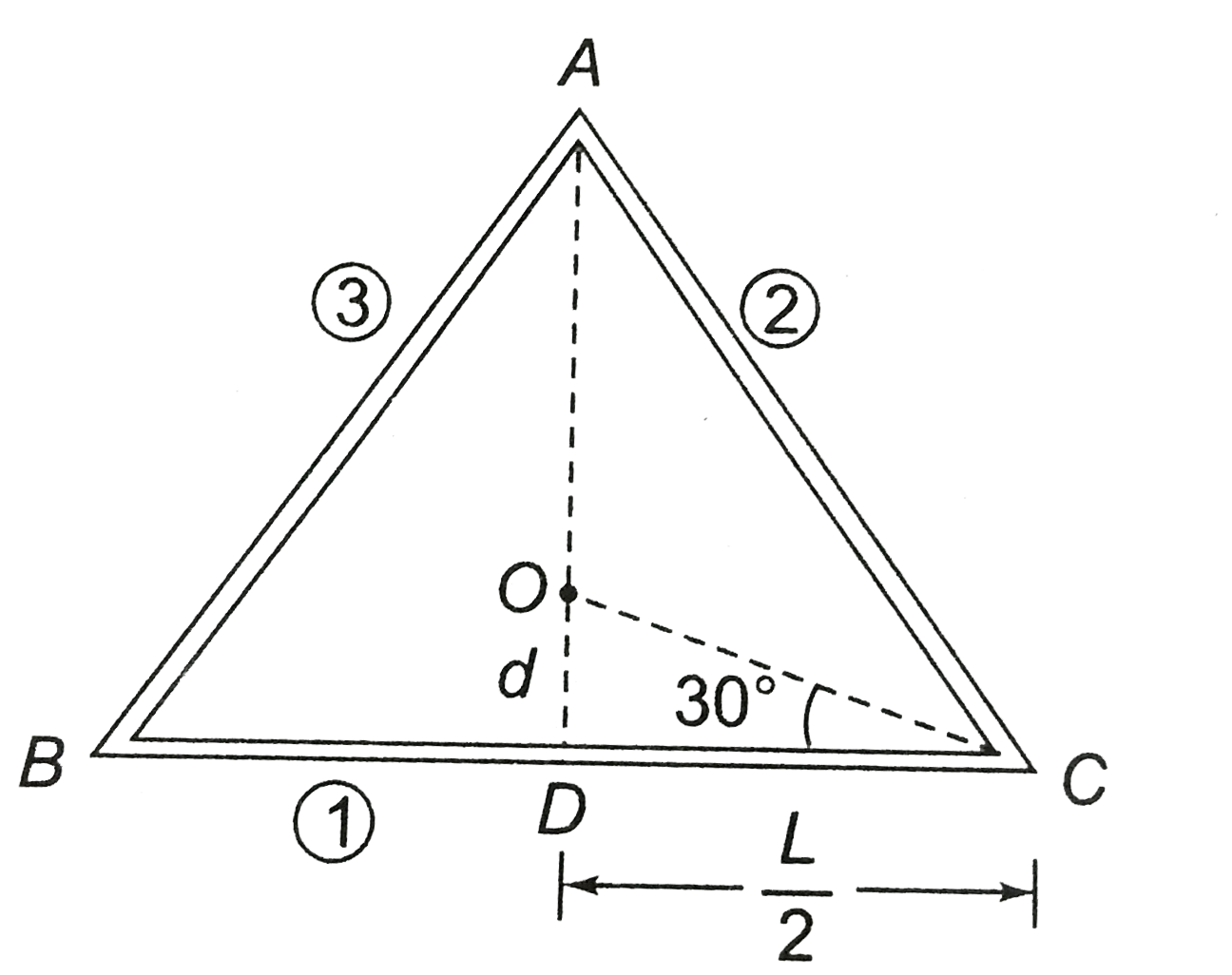
$M . I .$ of rod ( $1$ ), about axis through $O$
$I_{1} = \frac{M L^{2}}{12} + M d^{2} = \frac{M L^{2}}{12} + M {(\frac{1}{2 \sqrt{3}})}^{2} = \frac{M L^{2}}{6}$
${I n Δ O D C, {tan 30}^{\circ} = \frac{d}{L / 2} \Rightarrow d = \frac{L}{2 \sqrt{3}}}$
Similar anyalysis for two other rods
$I_{0} = 3 I_{1} = \frac{M L^{2}}{2}$
( $b$ )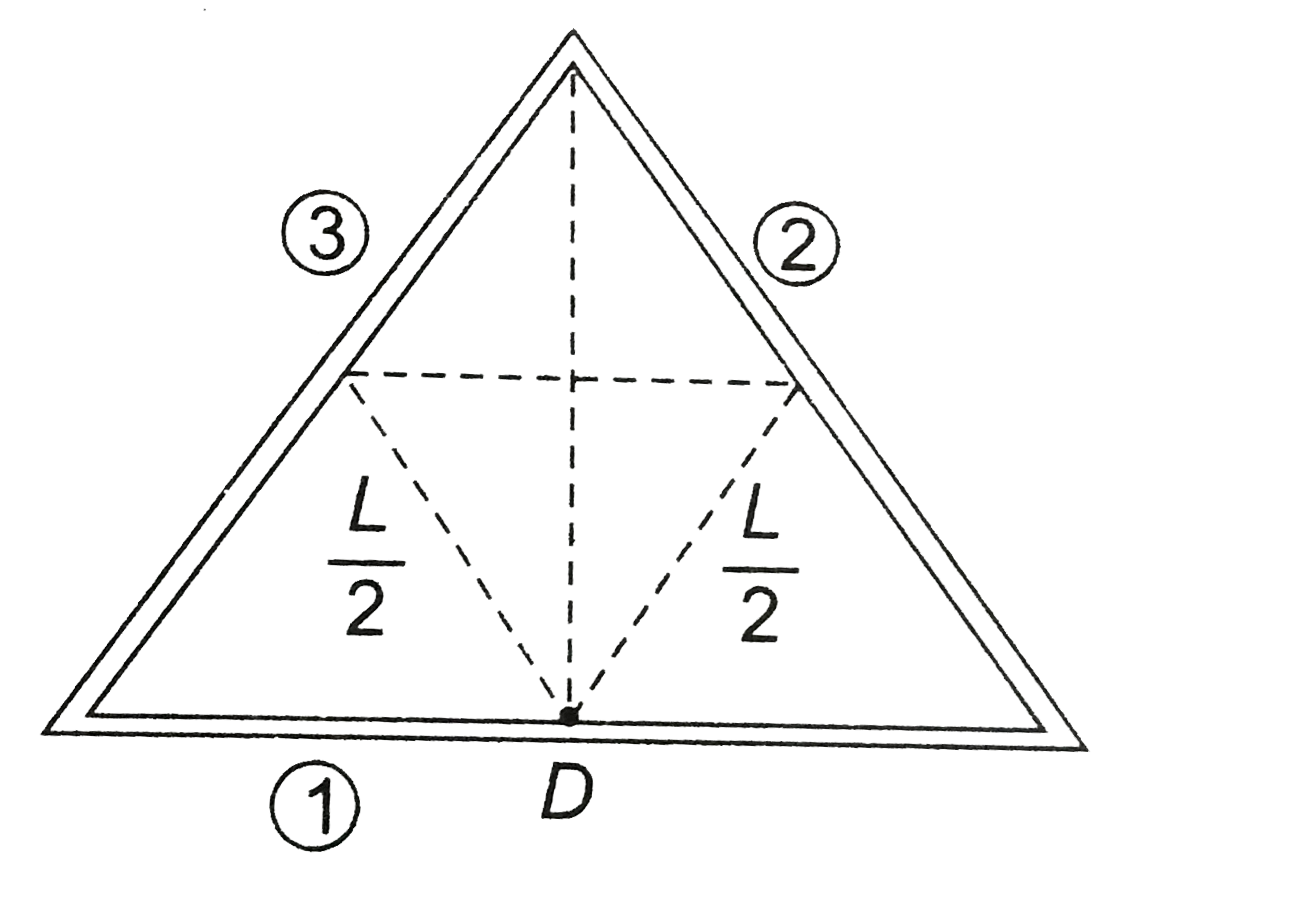
Axis is passing through $D$ and $⊥^{a r}$ to the plane
$I_{D} = I_{1} + I_{2} + I_{3}$
$I_{1} = \frac{M L^{2}}{12}$
$I_{2} = I_{3} = \frac{M L^{2}}{12} + M {(\frac{L}{2})}^{2} = \frac{M L^{2}}{3}$
$I_{D} = \frac{M L^{2}}{12} + \frac{M L^{2}}{3} \times 2 = \frac{3}{4} M L^{2}$
(If we join the mid-point of equilateral triangle of side $L$ , we get another equilateral triangle of side $L / 2$ .)
( $c$ )
Axis is passing through $A$ and $⊥^{a r}$ to the plane. For rods ( $2$ ) and ( $3$ ), the axis through $A$ is an axis passing through the end of rod and $⊥^{a r}$ to the length
$I_{2} = I_{3} = \frac{M L^{2}}{3}$
For rod ( $1$ )
$I_{1} = \frac{M L^{2}}{12} + M {(\frac{\sqrt{3} L}{2})}^{2} = \frac{5 M L^{2}}{6}$
$I_{A} = I_{1} + I_{2} + I_{3} = (\frac{5}{6} + \frac{1}{3} + \frac{1}{3}) = \frac{9 M L^{2}}{6} = \frac{3 M L^{2}}{2}$
Alternatively for parts ( $b$ ) and ( $c$ )

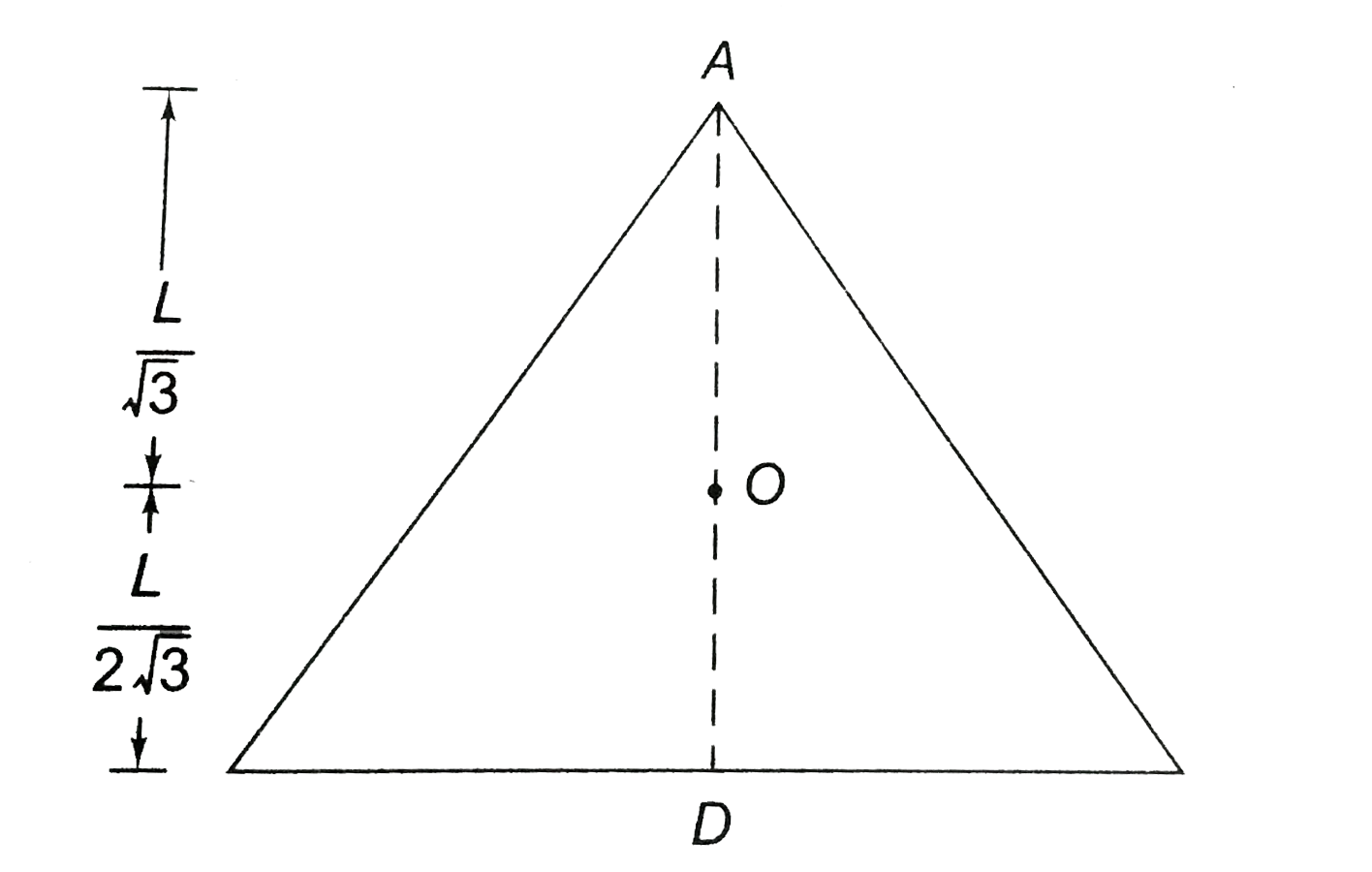
$O$ is the center of mass of system of rods
$I_{D} = I_{O} + 3 M {(\frac{L}{2 \sqrt{3}})}^{2} = \frac{M L^{2}}{2} + 3 M \frac{L^{2}}{12} = \frac{3 M L^{2}}{4}$
$I_{A} = I_{O} + 3 M {(\frac{L}{\sqrt{3}})}^{2} = \frac{M L^{2}}{2} + 3 M \frac{L^{2}}{3} = \frac{3 M L^{2}}{2}$

Updated on:21/07/2023